Come ridurre la frazione? Regole per tutte le situazioni
Senza la conoscenza di come ridurre una frazione e la disponibilità di un'abilità stabile nel risolvere tali esempi, è molto difficile imparare l'algebra a scuola. Più, più sulla conoscenza di base della riduzione delle frazioni ordinarie si sovrappongono nuove informazioni. I gradi appaiono prima, quindi i moltiplicatori, che in seguito diventano polinomi.
Come puoi non essere confuso? Rafforzare fondamentalmente le competenze in argomenti precedenti e gradualmente preparare la conoscenza su come ridurre le frazioni, che stanno diventando più complesse di anno in anno.
Conoscenza di base
Senza di loro, non sarai in grado di affrontare compiti di qualsiasi livello. Per capire come ridurre una frazione bisogno di capire due semplici punti. Primo: puoi solo ridurre i fattori. Questa sfumatura è molto importante quando i polinomi appaiono nel numeratore o nel denominatore. Quindi è necessario distinguere chiaramente dove si trova il moltiplicatore e dove si trova il termine.
Ad
Il secondo punto suggerisce che qualsiasi numero può essere rappresentato come moltiplicatore. Inoltre, il risultato della riduzione è una tale frazione, il cui numeratore e denominatore non può più essere ridotto.

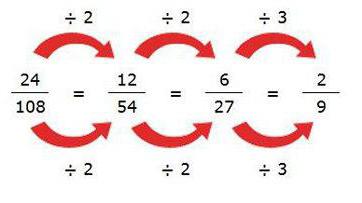
Regole per ridurre le frazioni ordinarie
Per cominciare vale la pena controllare se il numeratore è divisibile per denominatore o viceversa. Quindi è su questo numero che devi fare una riduzione. Questa è l'opzione più semplice.
Il secondo è l'analisi dell'aspetto dei numeri. Se entrambi terminano con uno o più zeri, possono essere ridotti di 10, 100 o mille. Qui puoi vedere se i numeri sono pari. Se è così, allora puoi tranquillamente tagliarne due.
La terza regola su come ridurre la frazione diventa la scomposizione in fattori primi del numeratore e denominatore. In questo momento, è necessario utilizzare attivamente tutte le conoscenze sui segni di divisibilità dei numeri. Dopo una tale decomposizione, rimane solo per trovare tutti i duplicati, moltiplicarli e fare una riduzione dal numero risultante.
Ad
Cosa succede se la frazione è un'espressione algebrica?
Ecco le prime difficoltà. Perché è qui che compaiono i termini, che possono essere identici ai moltiplicatori. Vogliono davvero tagliare, ma no. Prima di ridurre la frazione algebrica, deve essere trasformata in modo che abbia moltiplicatori.
Ciò richiederà diversi passaggi. Potrebbe essere necessario esaminarli tutti, e forse il primo offrirà un'opzione adatta.
Controlla se il numeratore e il denominatore o qualsiasi espressione in essi differiscono dal segno. In questo caso, devi solo calcolare il meno uno. Quindi ottieni gli stessi fattori che possono essere ridotti.
Vedi se il fattore comune può essere tolto dal polinomio dalle parentesi. Forse questo si tradurrà in una parentesi, che può anche essere accorciata, o sarà un monomio reso.
Prova a raggruppare i monomi per poi farne un fattore comune. Dopo di ciò, potrebbe risultare che i moltiplicatori appaiano che possono essere ridotti, oppure ripetere la rimozione degli elementi comuni.
Prova a guardare le formule di moltiplicazione abbreviata nella notazione. Con il loro aiuto, è facile convertire un polinomio in fattori.
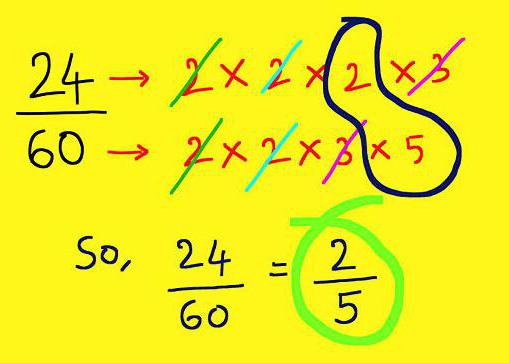
Sequenza di azioni con frazioni con gradi
Per comprendere facilmente la domanda su come ridurre una frazione con gradi, è necessario ricordare con fermezza le azioni di base con loro. Il primo di questi è legato alla moltiplicazione dei poteri. In questo caso, se le basi sono le stesse, gli indicatori devono essere sommati.
Ad
Il secondo è la divisione. Di nuovo, per coloro che hanno la stessa base, gli indicatori dovranno essere sottratti. E devi sottrarre dal numero che si trova nel dividendo, e non viceversa.
Il terzo è l'innalzamento al grado di laurea. In questa situazione, gli indicatori sono moltiplicati.
Una riduzione efficace richiederà anche la capacità di portare i gradi alla stessa base. Cioè, per vedere che quattro è due in un quadrato. O 27 - un cubo di tre. Perché è difficile tagliare 9 in un quadrato e 3 in un cubo. Ma se converti la prima espressione in (3 2 ) 2 , la riduzione avrà successo.