L'interpolazione è ... Definizione, caratteristiche di calcolo ed esempi di interpolazione

Molti di noi hanno dovuto affrontare termini incomprensibili in diverse scienze. Ma ci sono pochissime persone che non hanno paura di parole incomprensibili, ma al contrario ci incoraggiano e ci costringono a scavare sempre di più nella materia studiata. Oggi parleremo di un'interpolazione. Questo è un metodo per costruire grafici da punti noti, che consente, con una minima quantità di informazioni su una funzione, di prevedere il suo comportamento su sezioni specifiche della curva.

Prima di passare all'essenza della definizione stessa e di raccontarla in modo più dettagliato, ci addentriamo un po 'nella storia.

Storia di

L'interpolazione è nota fin dall'antichità. Tuttavia, questo fenomeno deve il suo sviluppo a molti dei più eminenti matematici del passato: Newton, Leibniz e Gregory. Hanno sviluppato questo concetto con l'aiuto di metodi matematici più avanzati disponibili al momento. Prima di ciò, l'interpolazione, ovviamente, veniva utilizzata e utilizzata nei calcoli, ma veniva eseguita in modi completamente imprecisi che richiedono una grande quantità di dati per costruire un modello più o meno vicino alla realtà.

Oggi possiamo anche scegliere quale metodo di interpolazione è più adatto. Tutto è stato tradotto in un linguaggio informatico, che con grande precisione può predire il comportamento di una funzione in una determinata area, limitata da punti noti.

L'interpolazione è un concetto piuttosto ristretto, quindi la sua storia non è così ricca di fatti. Nella prossima sezione capiremo che cos'è realmente l'interpolazione e in che cosa differisce dal suo opposto: estrapolazione.

Cos'è l'interpolazione?

Come abbiamo detto, questo è il nome generico per come costruire un grafico per punti. A scuola, questo viene fatto principalmente compilando una tabella, identificando i punti su un grafico e approssimativamente costruendo le linee che li connettono. L'ultima azione è fatta sulla base di considerazioni sulla somiglianza della funzione investigata con altri, sul tipo di grafici che conosciamo.

Tuttavia, ci sono altri modi più complessi e precisi per eseguire il compito di tracciare per punti. Quindi, l'interpolazione è in realtà una "previsione" del comportamento di una funzione in una particolare area, limitata da punti noti.

Esiste un concetto simile associato alla stessa area: estrapolazione. Rappresenta anche la previsione del grafico della funzione, ma oltre i punti noti del grafico. Con questo metodo, la previsione viene effettuata sulla base del comportamento della funzione su un intervallo noto e quindi questa funzione viene applicata anche all'intervallo sconosciuto. Questo metodo è molto pratico per l'uso pratico e viene utilizzato attivamente, ad esempio, in economia per prevedere gli alti e bassi del mercato e per prevedere la situazione demografica nel paese.

Ma ci siamo allontanati dall'argomento principale. Nella prossima sezione capiremo che tipo di interpolazione avviene e con l'aiuto di quali formule è possibile eseguire questa operazione.

Tipi di interpolazione

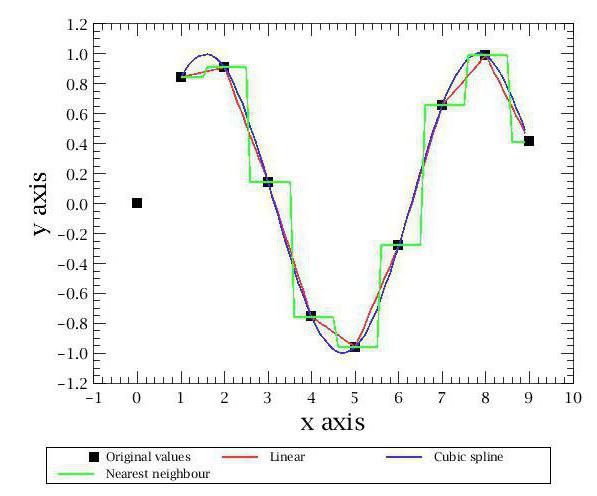
Il tipo più semplice è l'interpolazione più vicina. Con questo metodo otteniamo un grafico molto approssimativo costituito da rettangoli. Se hai visto almeno una volta la spiegazione del significato geometrico dell'integrale nel grafico, allora capirai di che tipo di forma grafica stiamo parlando.

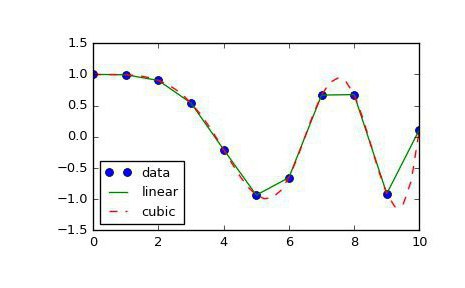
Inoltre, ci sono altri metodi di interpolazione. I più famosi e popolari sono associati ai polinomi. Sono più accurati e consentono di prevedere il comportamento di una funzione con un insieme di valori piuttosto scarso. Il primo metodo di interpolazione che consideriamo sarà l'interpolazione lineare da parte dei polinomi. Questa è la via più facile da questa categoria, e sicuramente ognuno di voi l'ha usata a scuola. La sua essenza sta nella costruzione di linee rette tra punti noti. Come è noto, una singola retta passa attraverso due punti del piano, la cui equazione può essere trovata sulla base delle coordinate di questi punti. Costruendo queste linee rette, otteniamo un grafico spezzato, che è in qualche modo, ma riflette i valori approssimativi delle funzioni e in termini generali coincide con la realtà. Ecco come viene eseguita l'interpolazione lineare.

Tipi di interpolazione complicati

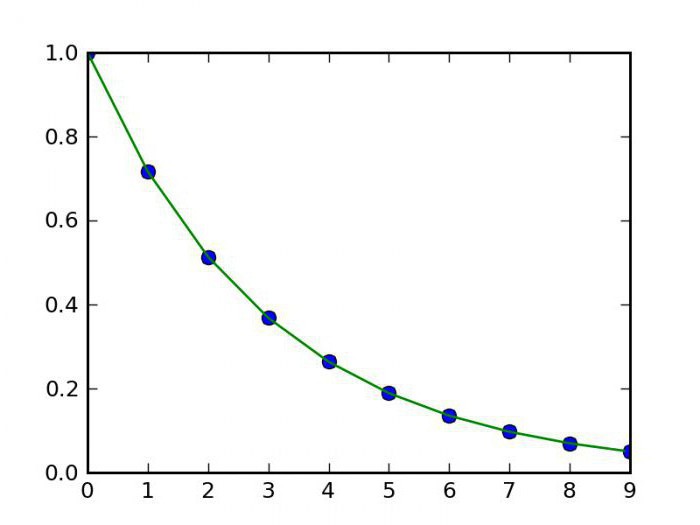
C'è un metodo di interpolazione più interessante, ma più complicato. Fu inventato dal matematico francese Joseph Louis Lagrange. Questo è il motivo per cui il calcolo dell'interpolazione che usa questo metodo prende il nome da lui: Interpolazione di Lagrange. L'attenzione qui è questa: se il metodo descritto nel paragrafo precedente utilizza solo una funzione lineare per il calcolo, allora la decomposizione di Lagrange implica anche l'uso di polinomi di grado più elevato. Ma non è così facile trovare le formule di interpolazione stesse per funzioni diverse. E più punti sono noti, più accurata è la formula di interpolazione. Ma ci sono molti altri metodi.

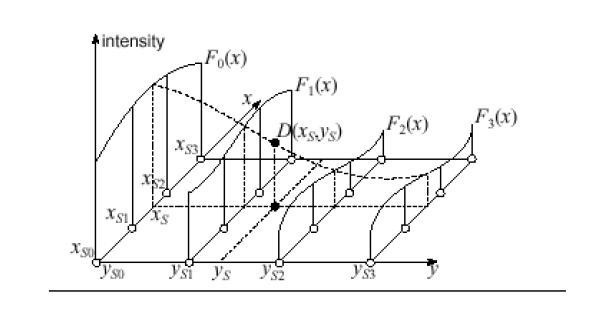
C'è anche un metodo di calcolo più perfetto e realistico. La formula di interpolazione utilizzata in esso è un insieme di polinomi, l'applicazione di ognuno dei quali dipende dall'area della funzione. Questo metodo è chiamato la funzione spline. Inoltre, ci sono anche modi per realizzare cose come le funzioni interpolanti di due variabili. Ci sono solo due metodi. Tra questi, l'interpolazione bilineare o doppia. Questo metodo ti consente di creare facilmente un grafico per punti in spazio tridimensionale. Altri metodi non influenzeranno. In generale, l'interpolazione è un nome universale per tutti questi metodi grafici, ma la varietà di modi in cui questa azione può essere eseguita li costringe a essere divisi in gruppi a seconda del tipo di funzione che è soggetta a questa azione. Cioè, l'interpolazione, un esempio di cui abbiamo considerato sopra, si riferisce ai metodi diretti. Esiste anche l'interpolazione inversa, che differisce in quanto ci consente di calcolare non la diretta, ma la funzione inversa (cioè x da y). Non prenderemo in considerazione le ultime opzioni, poiché è piuttosto difficile e richiede una buona base di conoscenze matematiche.

Ci rivolgiamo a forse una delle sezioni più importanti. Da esso apprendiamo come e dove l'insieme di metodi di cui stiamo discutendo viene applicato nella vita.

applicazione

La matematica è nota per essere la regina delle scienze. Pertanto, anche se non vedi per la prima volta il punto in determinate operazioni, questo non significa che siano inutili. Ad esempio, sembra che l'interpolazione sia una cosa inutile, con l'aiuto di cui possono essere costruiti solo grafici, di cui poche persone hanno bisogno ora. Tuttavia, per qualsiasi calcolo in ingegneria, fisica e molte altre scienze (ad esempio, biologia), è estremamente importante presentare un quadro abbastanza completo del fenomeno, pur avendo un insieme definito di valori. I valori sparsi lungo il grafico non danno sempre una chiara idea del comportamento di una funzione in una particolare area, i valori delle sue derivate e i punti di intersezione con gli assi. E questo è molto importante per molte aree della nostra vita con te.

E come è utile nella vita?

Questa domanda è molto difficile da rispondere. Ma la risposta è semplice: niente da fare. Questa conoscenza non ti sarà utile. Ma se comprendi questo materiale e i metodi con cui vengono eseguite queste azioni, eserciterai la tua logica, che è molto utile nella vita. La cosa principale non è la conoscenza in sé, ma le abilità che una persona acquisisce nel processo di apprendimento. Dopo tutto, non c'è da meravigliarsi se c'è un detto: "Vivi e impara".

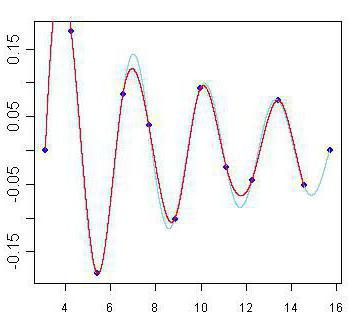
Concetti correlati

Puoi capire da te quanto sia importante (e ancora non perda la sua importanza) quest'area della matematica, guardando alla diversità di altri concetti correlati a questo. Abbiamo già parlato di estrapolazione, ma c'è anche un'approssimazione. Forse hai già sentito quella parola. In ogni caso, cosa significa, abbiamo anche discusso in questo articolo. Approssimazione, come l'interpolazione, è un concetto correlato alla costruzione di grafici di funzioni. Ma la differenza tra il primo e il secondo è che rappresenta la costruzione approssimativa di un grafico basato su grafici noti simili. Questi due concetti sono molto simili tra loro ed è più interessante studiarli.

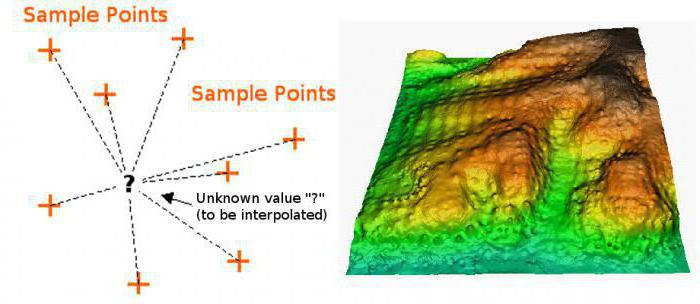
conclusione

La matematica non è una scienza così complessa come sembra a prima vista. È piuttosto interessante. E in questo articolo abbiamo provato a dimostrarlo. Abbiamo esaminato i concetti associati alla costruzione di grafici, abbiamo appreso quale doppia interpolazione è e smontata con esempi in cui viene utilizzata.