Analisi matematica e il suo ruolo nel mondo moderno

Storia di

La filosofia è considerata al centro di tutte le scienze, poiché includeva i primi germi di letteratura, astronomia, letteratura, scienze naturali, matematica e altre aree. Nel tempo, ogni area si è sviluppata indipendentemente, la matematica non ha fatto eccezione. Il primo "suggerimento" di analisi è considerato la teoria della decomposizione in valori infinitamente piccoli, a cui molte menti hanno cercato di avvicinarsi, ma aveva un carattere nebuloso e non aveva basi. Ciò è dovuto all'attaccamento alla vecchia scuola della scienza, che era rigorosa nella sua formulazione. Isaac Newton era molto vicino a formare la base, ma era in ritardo. Di conseguenza, la sua apparizione come sistema separato di analisi matematica è obbligata al filosofo Gottfried Leibniz. Fu lui che nei lavori presentati al mondo scientifico tali concetti, al minimo e al massimo, punti di inflessione e convessità del grafo della funzione, formularono le basi del calcolo differenziale. Da questo punto in poi, la matematica è ufficialmente divisa in elementare e superiore.

Analisi matematica I nostri giorni

Qualsiasi specialità, sia tecnica che umanitaria, include analisi nel corso di studio. La profondità dello studio varia, ma l'essenza rimane la stessa. Nonostante tutta l '"astrattezza", è uno dei pilastri su cui poggia la scienza naturale nella sua comprensione moderna. Con il suo aiuto, la fisica e l'economia sono state sviluppate, è in grado di descrivere e prevedere le attività della borsa, per aiutare a costruire un portafoglio azionario ottimale. Un'introduzione all'analisi matematica si basa su concetti elementari:

• set;
• operazioni di base;
• proprietà di operazioni su insiemi;
• funzioni (altrimenti, mappature);
• tipi di funzioni;
• sequenza;
• linee numeriche;
• limite di sequenza;
• proprietà dei limiti;
• continuità di funzione.

Vale la pena isolare concetti come set, punto, linea, piano separatamente. Tutti loro non hanno definizioni, in quanto sono i concetti di base su cui è costruita tutta la matematica. Tutto ciò che può essere fatto nel processo di lavoro è spiegare cosa significano esattamente nei singoli casi.

Limite come continuazione

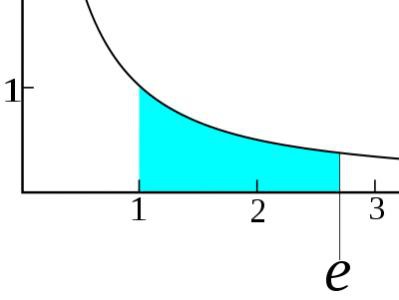Le basi dell'analisi matematica sono il limite. In pratica, è un valore al quale tende una sequenza o una funzione, si avvicina quanto desidera, ma non la raggiunge. È indicato da lim: consideriamo un caso speciale del limite della funzione: lim (x-1) = 0 come x → 1. Da questo semplice esempio, è chiaro che come x → 1, l'intera funzione tende a 0, poiché se sostituiamo il limite nella funzione stessa, otteniamo (1-1) = 0. Più in dettaglio, dai casi particolari elementari a quelli complicati, l'informazione viene presentata in una sorta di analisi "Bibbia" - le opere di Fichtenholz. Lì è considerato nel contesto dell'analisi matematica, i limiti, la loro derivazione e ulteriore applicazione. Ad esempio, la derivazione del numero e (costante di Eulero) sarebbe impossibile senza la teoria dei limiti. Nonostante l'astrattezza dinamica della teoria, i limiti sono attivamente utilizzati nella pratica nella stessa economia e sociologia. Ad esempio, non si può fare a meno di loro quando si addebita l'interesse su un deposito bancario.