Paradox Monty Hall. La matematica più imprecisa

La teoria della probabilità è una branca della matematica che è pronta a confondere i matematici stessi. A differenza del resto, dogmi esatti e irremovibili di questa scienza, quest'area pullula di estraneità e inesattezze. In questa sezione, un nuovo paragrafo è stato aggiunto di recente: il paradosso di Monty Hall. Questo è, in generale, un compito, ma è risolto in un modo completamente diverso da quello scolastico o universitario a cui siamo abituati.

Storia di origine

Oltre il paradosso di Monty Hall, le persone hanno rotto le loro teste dal lontano 1975. Ma vale la pena partire dal 1963. In quel momento è uscito uno show televisivo intitolato Let's make deal, che si traduce in "Facciamo un patto". Il suo ruolo era nientemeno che Monty Hall, che ha gettato gli spettatori a volte intrattabili enigmi. Uno dei più sorprendenti fu quello che presentò nel 1975. Il compito è diventato parte della teoria matematica della probabilità e dei paradossi che si inseriscono nella sua struttura. Vale anche la pena notare che questo fenomeno ha portato a forti discussioni e critiche severe da parte degli scienziati. Il paradosso di Monty Hall è stato pubblicato sulla rivista Parade nel 1990 e da allora è diventato un problema ancora più dibattuto e controverso di tutti i tempi e di tutti i popoli. Bene, ora procediamo direttamente alla sua formulazione e interpretazione.

Formulazione del problema

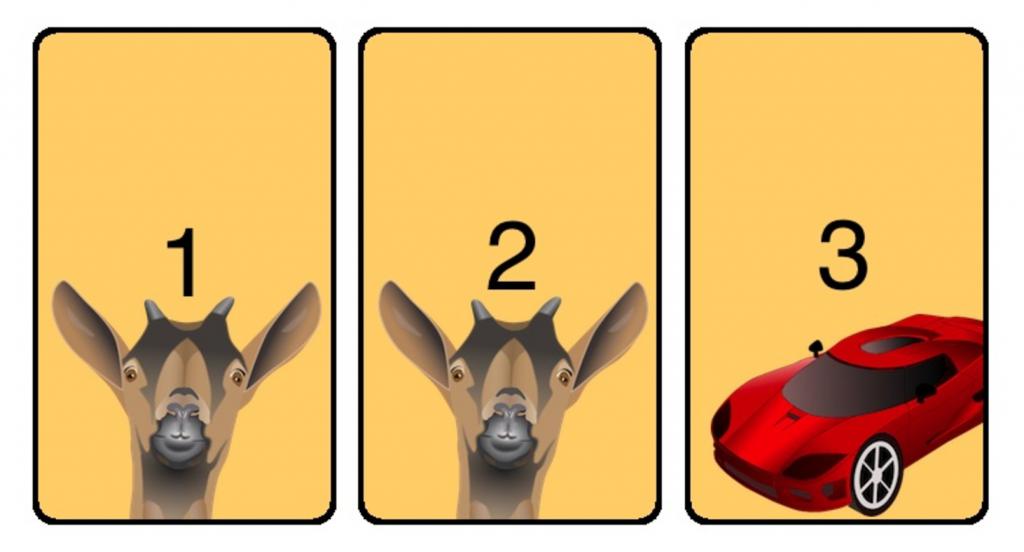
Ci sono molte interpretazioni di questo paradosso, ma abbiamo deciso di presentarti un classico, che è stato mostrato nel programma stesso. Quindi, prima che tu sia a tre porte. Dietro a una di esse c'è una macchina, dietro alle altre due su una capra. Il facilitatore ti invita a scegliere una delle porte e, diciamo, tu rimani al numero 1. Finora non sai cosa c'è dietro questa primissima porta, da quando apri il terzo, e mostri che dietro c'è una capra. Di conseguenza, non hai ancora perso, perché non hai scelto la porta che nasconde l'opzione perdente. Di conseguenza, le tue possibilità di ottenere una macchina aumentano.

Ma qui il leader ti offre di cambiare la decisione. Prima di avere due porte, per una capra, per un altro premio desiderato. Questa è l'essenza del problema. Sembra che qualsiasi delle due porte scelte, le probabilità siano 50 a 50. Ma in effetti, se cambi la decisione, la probabilità che vinci sarà maggiore. Come così?

Una spiegazione del paradosso di Monty Hall

La prima scelta che fai in questo gioco è casuale. Non puoi neanche lontanamente immaginare quale delle tre porte sia un premio nascosto, quindi indica casualmente la prima. Il leader, a sua volta, sa dove sono le cose. Ha una porta con un premio, una porta che hai indicato e una terza senza premio, che ti apre come primo indizio. Il secondo suggerimento risiede nella sua proposta di cambiare la scelta.

Ora non sceglierai uno dei tre a caso, ma puoi anche cambiare la tua decisione per ottenere il premio desiderato. È il vantaggio che dà alla persona la convinzione che l'auto non sia realmente dietro la porta che ha scelto, ma dietro l'altra. Questa è l'essenza del paradosso, perché, di fatto, è necessario scegliere (almeno da due, e non da tre) a caso, ma le possibilità di vincere aumentano. Come mostrano le statistiche, dei 30 giocatori che hanno cambiato idea, hanno vinto una macchina 18. E questo è del 60%. E delle stesse 30 persone che non hanno cambiato la decisione - solo 11, cioè il 36%.

Trattamento in numeri

Ora diamo al paradosso di Monti Hall una definizione più precisa. La prima scelta del giocatore apre la porta in due gruppi. La probabilità che il premio si trovi dietro la porta che hai scelto è 1/3, e dietro quelle porte che rimangono 2/3. Il facilitatore apre ulteriormente una delle porte del secondo gruppo. Così trasferisce la probabilità residua, 2/3, a una porta che non hai scelto e che non ha aperto. È logico che dopo tali calcoli sarà più vantaggioso cambiare la tua decisione. Ma è importante ricordare che c'è ancora una possibilità di perdere. A volte l'astuzia principale, dal momento che è possibile colpire inizialmente il corretto, la porta premio, e dopo si rifiuta volontariamente.

Siamo tutti abituati al fatto che la matematica, in quanto scienza esatta, va di pari passo con il buon senso. Ecco i numeri che lo rendono, non le parole, le formule esatte, non le vaghe riflessioni, le coordinate, non i dati relativi. Ma la sua nuova sezione chiamata teoria della probabilità ha fatto esplodere l'intero schema familiare. I compiti di quest'area, a noi sembra, non investono nel quadro del buon senso e contraddicono completamente tutte le formule e i calcoli. Proponiamo di seguito per familiarizzare con altri paradossi della teoria della probabilità, che hanno qualcosa in comune con quello che è stato descritto sopra.

Paradosso di ragazzo e ragazza

Il problema, a prima vista, è assurdo, ma obbedisce rigorosamente a una formula matematica e ha due possibili soluzioni. Quindi, un certo uomo ha due figli. Uno di loro è probabilmente un ragazzo. Qual è la probabilità che il ragazzo sia il secondo?

Opzione 1. Consideriamo tutte le combinazioni di due bambini in una famiglia:

• Ragazza / ragazza
• Ragazza / ragazzo
• Ragazzo / ragazza
• Ragazzo / ragazzo

La prima combinazione ovviamente non ci soddisfa, quindi, in base agli ultimi tre, otteniamo una probabilità di 1/3 che il secondo figlio sarà un piccolo uomo.

Opzione 2. Se in pratica immaginiamo un caso del genere, dopo aver scartato le frazioni e le formule, allora, basandoci sul fatto che sulla Terra ci sono solo due sessi, la probabilità che il secondo figlio sia un maschio è 1/2.

Il paradosso della bella addormentata

Questa esperienza ci mostra quanto sia famoso poter manipolare le statistiche. Quindi, la bella addormentata viene iniettata con un sonnifero e viene lanciata una moneta. Se un'aquila cade, allora si sveglia e l'esperimento si ferma. Se le code cadono, allora la svegliano, facendo subito la seconda iniezione, e lei dimentica che si è svegliata, e dopo di che si è risvegliata solo il secondo giorno. Dopo un completo risveglio alla "bellezza", non si sa quale giorno abbia aperto gli occhi, o qual è la probabilità che la moneta cadesse come una coda. Secondo la prima variante della soluzione, la probabilità di ottenere una coda (o un'aquila) è 1/2. L'essenza della seconda opzione è che, se conduci l'esperimento 1000 volte, allora nel caso di un'aquila, la "bellezza" sarà risvegliata 500 volte, e con una rara - 1000. Ora la probabilità della croce è 2/3.