Paradossi di Zenone di Elea: descrizione, significato e fatti interessanti

I paradossi di Zenone furono perplessi da molti scienziati e filosofi fino al XVII secolo. E fino ad ora, molti scienziati hanno discusso dell'infinito, la struttura dello spazio e del tempo, sebbene tutto sia partito da alcune affermazioni paradossali che hanno posto inizialmente l'empasse logico di una persona intelligente.

La storia dei paradossi di Zenone

Zenon di Elea - il filosofo dell'antica Hellas, allievo del fondatore della scuola eleatica - Parmenide. Visse dal 515 al 450 aC, si conosce molto poco della sua vita. Nato nella città di Elee, nel sud Italia. Secondo Platone, Zenone visitò Atene e incontrò Socrate. Era famoso per la sua aporia, nella forma in cui era stato formulato il famoso paradosso di Zenone. Le aporie di Zenone sono ragionamenti paradossali, la stessa parola "aporia" dal greco significa "disperazione".

Nei tempi antichi, i contemporanei contavano 40 affermazioni paradossali, e solo 9 sopravvissero ai nostri giorni, il più famoso - 4. Le aporie di Zenone furono apprese attraverso le opere di Aristotele, e anche da filosofi come Diogene di Laerte, Platone, Filopone, Simplicio. A proposito, vale la pena menzionare la stessa scuola Elea, a cui Zeno apparteneva. I suoi insegnamenti principali dicono che ogni cambiamento è un'illusione, l'essere è uno e non cambia. Zenone disse che la vera realtà è eterna e immutabile, e può essere compresa solo con l'aiuto della ragione e della logica. Pertanto, molte delle aporie di Zenone sono dedicate al movimento, in cui egli mostra che il movimento (o il cambiamento), dal punto di vista della logica, non esiste.

Paradossi su movimento e tempo

"La gara di Achille e la tartaruga" - uno dei paradossi più famosi di Zenone. Probabilmente ogni scolaro lo conosce. Ci sono anche tali aporie di Zenone come "Frecce Volanti", "Dicotomia" e altre. Sono dedicati al movimento, discusso e studiato per due millenni. Molti studi sono stati dedicati a loro, e fino al 17 ° secolo, i pensatori non potevano confutare questa logica ingegnosa.

Il problema è stato risolto dopo l'idea del calcolo differenziale, proposta da Newton e Leibniz. Esiste il concetto di "limite", quindi la differenza tra il tempo di divisione e la divisione di un determinato percorso in segmenti è diventata chiara. Inoltre, il mistero è stato risolto quando gli scienziati hanno imparato a usare quantità infinitamente piccole. L'aporia di Zenone da allora ha generato molte varianti diverse. Inoltre, forse aggiunto alcuni dettagli. Elencheremo i paradossi di Zenone che sono sopravvissuti ai nostri giorni e descriviamo brevemente la loro essenza. In ogni caso, prova a farlo.

Il paradosso di Zenone di Achille e la tartaruga

L'eroe dei miti dell'antica Grecia, Achille, compete in velocità con una tartaruga. Le condizioni sono tali che la tartaruga inizia un po 'oltre, Achille è a 1000 passi da essa.

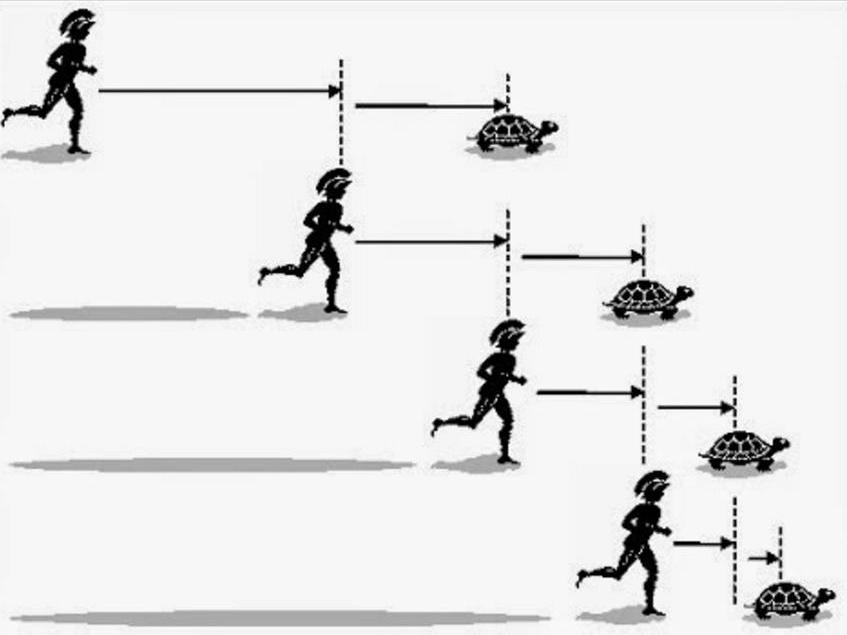
Per raggiungere la tartaruga, Achille deve prima raggiungere il punto da cui è partita la tartaruga. Ma non appena raggiunge il punto, la tartaruga avrà il tempo di strisciare di 100 passi. Questa distanza, che lei ha strisciato, deve ancora essere superata da Achille, ma a quel punto avrà strisciato di 10 gradini più in là e così via. Il numero di tali segmenti che Achille deve superare, secondo Zeno, può essere infinito, perché la dimensione di questi segmenti sarà sempre ridotta a valori infinitamente piccoli.

Si scopre che se segui questa logica, l'antico eroe greco non raggiungerà mai la tartaruga. Il paradosso di Zenone è l'esistenza di un numero infinito di segmenti infinitamente piccoli, ma nella vita reale il corridore sorpasserà sicuramente l'animale che si muove lentamente.

Freccia volante

Questo paradosso è chiamato Arrow. Questa è un'altra aporia che Zeno ha formulato in circa le seguenti parole. Se qualcosa è in movimento, allora si sposta nel punto in cui si trova da solo, o si sposta dove non esiste. Ma non può muoversi nel posto che occupa. Poiché ad ogni secondo occupa tutto il posto. Ma nel posto in cui non è, non può muoversi. Pertanto, il movimento stesso è impossibile.

Secondo Zeno, la freccia, quando vola, è simultaneamente a riposo. Perché in ogni momento occupa lo stesso spazio, uguale ad esso. Cioè, una freccia rimane a riposo rispetto al luogo in cui si trova in un determinato periodo di tempo. Si scopre che la freccia volante è immobile. Se lei è immobile in un dato momento, significa che lei è a riposo e in altri momenti. E non c'è quel momento in cui la freccia si è mossa.

dicotomia

Il paradosso, che verrà fornito di seguito, è chiamato "dicotomia". Tradotto dalla lingua greca, significa "dividere in due" ed è stato dato da Aristotele. Questa aporia si sviluppa all'incirca nello stesso modo del paradosso di Zenone di Achille e della tartaruga.

L'originale dice del corridore, che non è nemmeno in grado di iniziare, perché il movimento, secondo Zeno, non esiste. Ma c'è anche un'opzione comune per attraversare la stanza.

Per attraversare una stanza, devi prima attraversare metà della stanza. Ci vorrà una certa unità di tempo. Dopodiché, rimarrà una certa distanza, dovrai superarne la metà per un'altra unità di tempo. Quindi la parte del percorso che restava rimane da dividere in due e la metà di questo segmento nello stesso tempo. Poi di nuovo c'è una certa distanza, metà della quale deve essere attraversata. Si scopre che la stanza può essere attraversata indefinitamente.

Due colonne nello stadio

Due colonne di persone, della stessa lunghezza, si muovono in parallelo con la stessa velocità in direzioni opposte. Secondo Zeno, il tempo che scadrà quando le colonne passano l'un l'altro è uguale alla metà del tempo in cui una persona deve passare per l'intera colonna.

Risoluzione dei paradossi di Zenone

Delle quattro aporie sopra elencate, le prime tre erano più conosciute. Il quarto è apparso a causa di una comprensione errata della natura del moto relativo.

Tutta l'aporia può essere facilmente confutata sperimentalmente. Niente impedisce di attraversare la stanza, rilasciare la freccia e sorpassare la tartaruga.

Considera il paradosso associato all'incrocio di una stanza. Certo, se dividi la distanza a metà e vai a metà, ci vorrà un certo periodo di tempo. Ci sarà ancora una distanza, che deve anche essere divisa in due e metà passaggio. Ma per questa volta ci vorrà la metà del tempo. Più piccola sarà la distanza da coprire, più il tempo per il suo passaggio sarà ridotto. Si scopre che quando si attraversa una stanza alla fine, è necessario un numero illimitato di periodi di tempo infinitamente piccoli. Ma se si sommano tutti i segmenti, si ottiene un certo numero - sarà il tempo trascorso attraversando la stanza. Risulta, è abbastanza possibile attraversare la stanza per un certo periodo di tempo. Questa dimostrazione è simile alla ricerca del limite nel calcolo differenziale. L'antico filosofo greco Zenone riteneva erroneamente che il passaggio di distanze infinitamente piccole richiedesse sempre lo stesso tempo.

Per quanto riguarda il paradosso di Zeno, "The Flying Arrow", Aristotele lo ha criticato, sostenendo che ogni momento del tempo non può essere indivisibile da solo. Ha anche detto che il ragionamento di Zenone è che se tutto ciò che occupa un posto uguale rimane a riposo, e se ciò che è in movimento prende sempre lo stesso posto in qualsiasi momento, allora la freccia è immobile, errata.

Effetto quantico

I paradossi di Zenone sono stati confutati nel tempo da molti scienziati. Ma hanno comunque dato un contributo preciso alla scienza. In fisica quantistica al momento esiste una cosa come il paradosso quantistico di Zenone. Sta nel fatto che se osservi una particella instabile, ad esempio, per effettuare misurazioni, controlla se una particella è decaduta o meno, quindi c'è un rallentamento nel decadimento radioattivo.

Si presume che se si osserva continuamente una particella, non si può interrompere affatto. Negli anni '90 del secolo scorso, questo effetto quantistico è stato confermato usando una serie di esperimenti.