Congettura di Poincaré: storia del problema, prova, significato

A scuola, tutti conoscono i concetti del teorema e dell'ipotesi. Di regola, le leggi più semplici e primitive sono influenzate nella vita, mentre i matematici fanno ipotesi molto complesse e pongono problemi interessanti. Non sempre, loro stessi riescono a trovare soluzioni e prove, e in alcuni casi i loro seguaci e colleghi hanno combattuto per molti anni.

L'Clay Institute nel 2000 compilò una lista di 7 cosiddette sfide del millennio per analogia con l'elenco di ipotesi compilate nel 1900. Quasi tutti questi compiti sono stati risolti e solo uno di essi è migrato alla versione aggiornata. Ora l'elenco dei problemi è il seguente:

• Congettura di Hodge;
• uguaglianza delle classi P e NP;
• Congettura di Poincaré;
• Teoria di Yang-Mills;
• Ipotesi di Riemann;
• l'esistenza e la scorrevolezza di risolvere le equazioni di Navier-Stokes;
• Congettura di Birch-Swinnerton-Dyer.

Tutti appartengono a diverse discipline all'interno della matematica e sono importanti. Ad esempio, le equazioni di Navier-Stokes si riferiscono all'idrodinamica, ma in pratica possono descrivere il comportamento di una sostanza nel magma terrestre o essere utili nel predire il tempo. Ma tutti questi problemi stanno ancora cercando la loro prova o negazione. Tranne uno.

Teorema di Poincaré

È piuttosto difficile spiegare con parole semplici qual è il problema, ma puoi provare. Immagina una sfera, ad esempio una bolla. Tutti i punti della sua superficie sono equidistanti dal suo centro, che non gli appartiene. Ma questo è un corpo bidimensionale, e l'ipotesi parla di un tridimensionale. È già impossibile immaginarlo, ma abbiamo una matematica teorica. In questo caso, ovviamente, tutti i punti di questo corpo verranno rimossi dal centro.

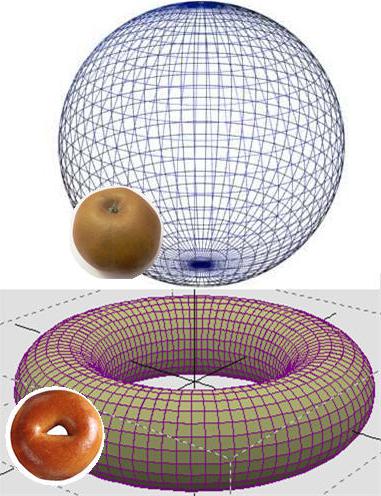
Questo problema riguarda la topologia: la scienza delle proprietà delle forme geometriche. E uno dei termini fondamentali in esso è l'omeomorfismo, cioè un alto grado di somiglianza. Per fare un esempio, puoi immaginare una palla e un toro. Una figura non può essere ottenuta da un'altra, evitando rotture, ma il cono, il cubo o il cilindro del primo può essere ottenuto abbastanza facilmente. Ecco l'ipotesi di Poincaré ed è dedicato a queste metamorfosi con una sola differenza: stiamo parlando di spazio e corpi multidimensionali.

Storia di

Matematico francese Henri Poincaré studiato vari campi della scienza. Circa i suoi risultati può dire, ad esempio, il fatto che indipendentemente da Albert Einstein, ha presentato le disposizioni principali teoria della relatività speciale. Nel 1904, sollevò il problema di dimostrare che qualsiasi corpo tridimensionale, che possiede certe proprietà di una sfera, è esattamente fino alla deformazione. Più tardi fu ampliato e generalizzato, e divenne un caso speciale dell'ipotesi di Thurston formulata nel 1982.

formulazione

Inizialmente, Poincaré lasciò una tale affermazione: ogni molteplicità tridimensionale compatta, semplicemente connessa senza un confine, è omeomorfa a una sfera tridimensionale. Successivamente è stato ampliato e generalizzato. Eppure per molto tempo è stato il compito originale a causare i maggiori problemi, e fu risolto solo 100 anni dopo la sua apparizione.

Interpretazione e significato

Questo è l'omeomorfismo, è già stato discusso. Ora vale la pena parlare di compattezza e singolarità. Il primo significa solo che la varietà ha dimensioni limitate, non può essere continuamente e allungata all'infinito.

Per quanto riguarda l'unicità, puoi provare a dare un semplice esempio. La sfera bidimensionale - la mela - ha una proprietà interessante. Se si prende la solita gomma da masticare chiusa e si attacca alla superficie, la deformazione liscia può essere ridotta a un punto. Questa è la proprietà dell'unicità, ma per presentarla in relazione a spazio tridimensionale abbastanza difficile.

Parlando in modo semplice, il problema era dimostrare che la singolarità è una proprietà unica per la sfera. E se, relativamente parlando, l'esperienza con un elastico si è conclusa con un tale risultato, allora il corpo è omeomorfo ad esso. Per quanto riguarda l'applicazione di questa teoria alla vita, Poincaré credeva che l'Universo, in un certo senso, fosse una sfera tridimensionale.

Prova di

Non pensare alle decine di matematici che hanno lavorato in tutto il mondo, nessuno ha avanzato una virgola, affrontando questo problema. Al contrario, c'erano dei progressi e alla fine ha portato a un risultato. Lo stesso Poincaré non ha avuto il tempo di finire il lavoro, ma la sua ricerca ha seriamente avanzato l'intera topologia.

Negli anni '30 tornò l'interesse per l'ipotesi. Prima di tutto, la formulazione è stata estesa a "spazio n-dimensionale", e in seguito l'American Whitehead ha riportato prove di successo, in seguito abbandonandolo. Negli anni 60-70, due matematici contemporaneamente - Smale e Stallings - quasi simultaneamente, ma in modi diversi svilupparono una soluzione per tutti e più di 4.

Nel 1982, e per 4, sono state trovate prove, ne sono rimaste solo 3. Nello stesso anno Thurston formulò l'ipotesi della geometrizzazione e la teoria di Poincaré divenne il suo caso particolare.

Poi il lavoro è stato in qualche modo in fase di stallo - l'americano Richard Hamilton ha proposto di utilizzare il flusso di Ricci nella soluzione, ma si è imbattuto in difficoltà e non ha completato la ricerca.

Per 20 anni l'ipotesi di Poincaré fu come dimenticata. Nel 2002, il matematico russo Grigori Perelman presentò una soluzione in termini generali, sei mesi dopo facendo alcune aggiunte. Più tardi, questa prova è stata testata e portata a "brillare" dagli scienziati americani e cinesi. E lo stesso Perelman sembrava aver perso ogni interesse per il problema, sebbene avesse risolto il problema più generale della geometrizzazione, per il quale la congettura di Poincaré è solo un caso speciale.

Riconoscimento e valutazione

Certo, questo è diventato immediatamente una sensazione, perché la soluzione di uno dei Millennium Problems semplicemente non poteva essere trascurata. Ancora più sorprendente è il fatto che Gregory Perelman abbia rifiutato tutti i premi e i premi, dicendo che aveva già una vita meravigliosa. Nella mente della gente comune, è diventato immediatamente un esempio di quel geniale mezzo pazzo che è interessato solo alla scienza.

Tutto ciò ha causato molta discussione sulla stampa e sui media, che la popolarità del matematico è diventata sua. Nell'estate del 2014, c'erano informazioni che Perelman andò a lavorare in Svezia, ma questo risultò essere solo una voce, vive ancora modestamente a San Pietroburgo e difficilmente comunica con nessuno. Tra i premi assegnati a lui c'erano non solo il Clay Institute Prize, ma anche la prestigiosa Fields Medal, ma ha rifiutato tutto. Tuttavia, Hamilton, che, secondo le stime di Perelman, non apportò contributi meno importanti alla dimostrazione, non fu nemmeno dimenticato. Nel 2009 e nel 2011 ha anche vinto prestigiosi premi e riconoscimenti.

Riflessione culturale

Nonostante il fatto che per i cittadini comuni sia la dichiarazione e la soluzione di questo problema non abbiano molto senso, le prove sono diventate note piuttosto rapidamente. Nel 2008, il regista giapponese Masahito Kasuga ha filmato il documentario "L'incanto dell'ipotesi di Poincaré" in questa occasione, dedicato ai 100 anni di tentativi per risolvere questo problema.

Molti matematici coinvolti in questo problema hanno preso parte alle riprese, ma il personaggio principale, Grigory Perelman, non ha voluto farlo. Anche gli amici più o meno intimi erano coinvolti nella sparatoria. Il film documentario, uscito sugli schermi in seguito alla risonanza pubblica sul rifiuto dello scienziato di accettare il premio, ha guadagnato fama in certi ambienti e ha anche ricevuto diversi riconoscimenti. Per quanto riguarda cultura di massa, la gente comune si chiede ancora quali argomenti il ​​matematico di Pietroburgo è stato guidato, rifiutando di prendere soldi quando potrebbe darlo via, per esempio, alla carità.