Probabilità di un evento Determinazione della probabilità di un evento

Inizialmente, essendo solo una raccolta di informazioni e osservazioni empiriche del gioco dei dadi, la teoria della probabilità divenne una scienza solida. Il primo a darle il quadro matematico erano Farm e Pascal.

Dal pensare all'eterno alla teoria della probabilità

Due personalità a cui la teoria della probabilità deve molte formule fondamentali, Blaise Pascal e Thomas Bayes, sono conosciute come persone profondamente religiose, quest'ultima essendo un prete presbiteriano. Apparentemente, il desiderio di questi due scienziati di dimostrare l'errore di opinione su una certa fortuna, dando fortuna ai loro animali domestici, ha dato impulso alla ricerca in questo settore. Dopo tutto, infatti, qualsiasi gioco d'azzardo con le sue vincite e perdite è solo una sinfonia di principi matematici.

Grazie all'eccitazione del cavaliere di Meré, che era ugualmente un giocatore e una persona non indifferente alla scienza, Pascal fu costretto a trovare un modo per calcolare la probabilità. De Mere era interessato a una domanda del genere: "Quante volte devi tirare due dadi in coppia per ottenere 12 punti in più del 50%?" La seconda domanda, estremamente interessata al gentiluomo: "Come dividere la scommessa tra i partecipanti al gioco incompiuto?" Naturalmente, Pascal ha risposto con successo a entrambe le domande di de Mere, che è diventato l'inconsapevole promotore dello sviluppo della teoria della probabilità. È interessante notare che la persona de Mere rimase nota in quest'area, e non in letteratura.

In precedenza, nessun matematico ha fatto alcun tentativo di calcolare le probabilità degli eventi, dal momento che si pensava che questa fosse solo una decisione che indicava il futuro. Blaise Pascal ha dato la prima definizione della probabilità di un evento e ha dimostrato che questa è una figura specifica che può essere dimostrata matematicamente. La teoria della probabilità è diventata la base per le statistiche ed è ampiamente utilizzata nella scienza moderna.

Che cos'è un incidente

Se consideriamo un test che può essere ripetuto un numero infinito di volte, possiamo definire un evento casuale. Questo è uno dei probabili risultati dell'esperimento.

L'esperienza è l'attuazione di azioni concrete in condizioni immutate.

Per lavorare con i risultati dell'esperienza, gli eventi sono solitamente indicati con le lettere A, B, C, D, E ...

Probabilità di un evento casuale

Per procedere alla parte matematica della probabilità, è necessario definire tutti i suoi componenti.

La probabilità di un evento è una misura numericamente espressa della possibilità che si verifichi un determinato evento (A o B) come risultato dell'esperienza. Denota la probabilità come P (A) o P (B).

Nella teoria della probabilità, distinto:

• si verifica un evento affidabile come risultato dell'esperimento P (Ω) = 1;
• l' evento impossibile non può mai verificarsi P (Ø) = 0;
• un evento casuale si trova tra un affidabile e impossibile, vale a dire, la probabilità della sua comparsa è possibile, ma non garantita (la probabilità di un evento casuale è sempre all'interno di 0≤P (A) ≤ 1).

Relazione tra eventi

Considerare sia l'una che la somma degli eventi A + B, quando un evento conta nell'implementazione di almeno uno dei componenti, A o B, o entrambi - A e B.

In relazione l'un l'altro, gli eventi possono essere:

• Uguale a
• Compatibile.
• Incompatibile.
• Opposto (si escludono a vicenda).
• Dipendente.

Se due eventi possono verificarsi con uguale probabilità, allora sono ugualmente possibili .

Se il verificarsi dell'evento A non annulla la probabilità del verificarsi dell'evento B, allora sono compatibili.

Se gli eventi A e B non si verificano mai contemporaneamente nella stessa esperienza, vengono chiamati incompatibili . Lanciare una moneta è un buon esempio: l'apparenza delle code è automaticamente la non apparizione di un'aquila.

La probabilità della somma di tali eventi incompatibili consiste nella somma delle probabilità di ciascuno degli eventi:

Р (А + В) = Р (А) + Р (В)

Se il verificarsi di un evento rende impossibile il verificarsi di un altro, allora vengono chiamati di fronte. Quindi uno di loro è designato come A, e l'altro - Â (leggi come "non A"). Il verificarsi dell'evento A significa che non si è verificato. Questi due eventi formano un gruppo completo con una somma di probabilità pari a 1.

Gli eventi dipendenti hanno un'influenza reciproca, riducendo o aumentando la probabilità l'uno dell'altro.

Relazione tra eventi. esempi

Con esempi è molto più facile comprendere i principi della teoria della probabilità e una combinazione di eventi.

L'esperienza che verrà svolta è quella di tirare fuori le palle dalla scatola, e il risultato di ogni esperienza è un risultato elementare.

Un evento è uno dei possibili risultati dell'esperienza: una palla rossa, una palla blu, una palla con il numero sei e così via.

Test numero 1. Ci sono 6 palle coinvolte, tre delle quali sono colorate di blu, i numeri dispari sono applicati a loro, e gli altri tre sono rossi con numeri pari.

Test numero 2. Ci sono 6 palline blu con numeri da uno a sei.

In base a questo esempio, puoi chiamare le combinazioni:

• Evento affidabile In spagnolo L'evento 2 "prendi la palla blu" è affidabile, poiché la probabilità che si verifichi è 1, poiché tutte le palle sono blu e non può mancare. Mentre l'evento "prendi la palla con il numero 1" - a caso.
• Evento impossibile In spagnolo №1 con l'evento di palline blu e rosse "ottenere la palla viola" è impossibile, perché la probabilità che si verifichi è 0.
• Eventi uguali In spagnolo Gli eventi numero 1 "prendi la palla con il numero 2" e "prendi la palla con il numero 3" sono ugualmente possibili, e gli eventi "prendi la palla con un numero pari" e "prendi la palla con il numero 2" hanno probabilità diversa.
• Eventi compatibili Due volte di fila per ottenere un sei nel processo di lancio di un dado - questi sono eventi compatibili.
• Eventi incompatibili Nello stesso isp. №1 gli eventi "prendi la palla rossa" e "prendi la palla con un numero dispari" non possono essere combinati nella stessa esperienza.
• Eventi opposti L'esempio più vivido di questo è il lancio di monete, quando tirare un'aquila equivale a non tirare fuori le code e la somma delle loro probabilità è sempre 1 (gruppo completo).
• Eventi dipendenti Quindi, in spagnolo. No. 1 può essere impostato per estrarre la palla rossa due volte di seguito. La sua estrazione o non estrazione per la prima volta influisce sulla probabilità di estrazione una seconda volta.

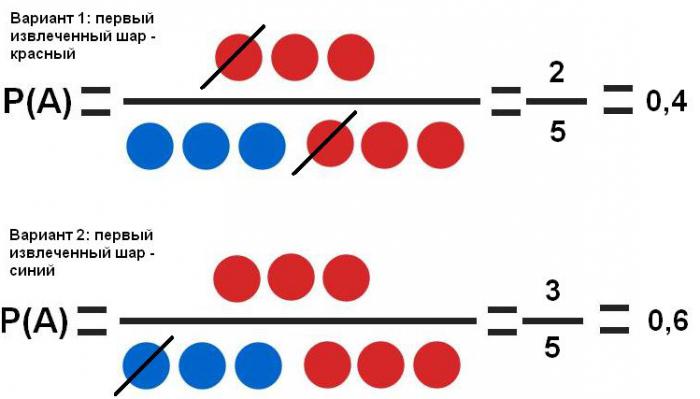
Si vede che il primo evento influisce significativamente sulla probabilità del secondo (40% e 60%).

Formula di probabilità di eventi

La transizione dalle riflessioni del preannunciamento ai dati precisi avviene trasferendo l'argomento sul piano matematico. Cioè, i giudizi su un evento casuale come "alta probabilità" o "probabilità minima" possono essere tradotti in dati numerici concreti. Tale materiale è già consentito per valutare, confrontare ed entrare in calcoli più complessi.

Dal punto di vista del calcolo, la determinazione della probabilità di un evento è il rapporto tra il numero di esiti positivi elementari e il numero di tutti i possibili esiti di esperienza relativi a un particolare evento. La probabilità è indicata da P (A), dove P indica la parola "probabilita", che viene tradotta dal francese come "probabilità".

Quindi, la formula della probabilità dell'evento:

P (A) = m / n,

Dove m è il numero di risultati favorevoli per l'evento A, n è la somma di tutti i risultati possibili per questa esperienza. In questo caso, la probabilità di un evento è sempre compresa tra 0 e 1:

0 ≤ P (A) ≤ 1.

Calcolo della probabilità di un evento. esempio

Prendi sp. No. 1 con le palle, come descritto in precedenza: 3 palline blu con numeri 1/3/5 e 3 rosse con numeri 2/4/6.

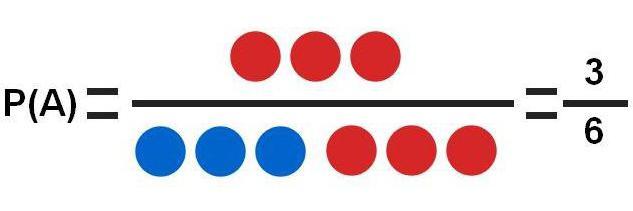
Sulla base di questo test, si possono prendere in considerazione diversi compiti:

• A - perdita della palla rossa. Ci sono 3 sfere rosse e ci sono 6 opzioni in totale: questo è l'esempio più semplice in cui la probabilità di un evento è P (A) = 3/6 = 0.5.
• B - perdita di un numero pari. Il numero totale di numeri pari è 3 (2,4,6), e il numero totale di opzioni numeriche possibili è 6. La probabilità di questo evento è P (B) = 3/6 = 0,5.
• C - perdita di un numero maggiore di 2. In totale ci sono 4 opzioni (3,4,5,6) rispetto al numero totale di risultati possibili 6. La probabilità dell'evento C è uguale a P (C) = 4/6 = 0,67.

Come si può vedere dai calcoli, l'evento C ha una maggiore probabilità, dal momento che il numero di risultati probabili positivi è maggiore rispetto a A e B.

Eventi non conformi

Tali eventi non possono apparire contemporaneamente nella stessa esperienza. Come in spagnolo No. 1 è impossibile ottenere contemporaneamente la palla blu e rossa. Cioè, puoi ottenere una palla blu o rossa. Allo stesso modo, nei dadi il pari non può apparire allo stesso tempo. un numero dispari.

La probabilità di due eventi è considerata come la probabilità della loro somma o prodotto. La somma di tali eventi A + B è considerata un tale evento, che consiste nella comparsa di un evento A o B, e il prodotto del loro AB - nell'aspetto di entrambi. Ad esempio, l'aspetto di due sei in una sola volta sulle facce di due dadi in un tiro.

La somma di più eventi è un evento che comporta la comparsa di almeno uno di essi. La creazione di diversi eventi è l'aspetto comune di tutti loro.

Nella teoria della probabilità, di regola, l'uso dell'unione "e" denota una somma, un'unione "o" - moltiplicazione. Le formule con esempi aiuteranno a comprendere la logica dell'aggiunta e della moltiplicazione nella teoria della probabilità.

Probabilità della somma di eventi incoerenti

Se viene considerata la probabilità di eventi incompatibili, la probabilità della somma di eventi è uguale all'addizione delle loro probabilità:

Р (А + В) = Р (А) + Р (В)

Ad esempio: calcola la probabilità che in sp. №1 con sfere blu e rosse cadrà il numero compreso tra 1 e 4. Non calcoliamo in un'unica azione, ma la somma delle probabilità dei componenti elementari. Quindi, in questa esperienza, solo 6 palle o 6 tutti i possibili risultati. I numeri che soddisfano la condizione sono 2 e 3. La probabilità di un 2 che cade è 1/6, la probabilità di 3 è anche 1/6. La probabilità che un numero compreso tra 1 e 4 cada è uguale a:

1/6 + 1/6 = 1/3

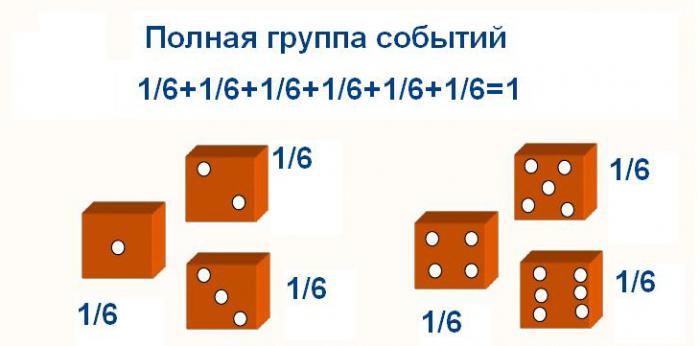
La probabilità della somma di eventi incompatibili del gruppo completo è 1.

Quindi, se nell'esperimento di un cubo sommiamo le probabilità di far cadere tutte le cifre, di conseguenza ne otteniamo una.

Questo vale anche per eventi opposti, ad esempio nell'esperienza con una moneta, in cui un lato è l'evento A, e l'altro è l'evento opposto, come è ben noto

Р (А) + Р (Â) = 1

Probabilità di produrre eventi incompatibili

La moltiplicazione delle probabilità viene utilizzata quando si considera il verificarsi di due o più eventi incompatibili in una singola osservazione. La probabilità che gli eventi A e B appaiano simultaneamente in esso è uguale al prodotto delle loro probabilità, o:

Р (А * В) = Р (А) * Р (В)

Ad esempio, la probabilità che in sp. # 1 come risultato di due tentativi, due volte una palla blu apparirà, uguale a

½ * ½ = ¼

Cioè, la probabilità di un evento, quando come risultato di due tentativi con l'estrazione di palle verranno estratte solo palline blu, è del 25%. È molto facile fare esperimenti pratici di questo compito e vedere se questo è davvero il caso.

Eventi congiunti

Gli eventi sono considerati congiunti quando l'aspetto di uno di essi può coincidere con l'aspetto dell'altro. Nonostante siano congiunti, viene considerata la probabilità di eventi indipendenti. Per esempio, lanciare due dadi può dare un risultato quando la figura 6 cade su entrambi, anche se gli eventi coincidono e compaiono allo stesso tempo, sono indipendenti l'uno dall'altro: solo un sei potrebbe cadere, il secondo non ha alcuna influenza su di esso.

La probabilità di eventi congiunti è considerata come la probabilità della loro somma.

Probabilità della somma di eventi congiunti. esempio

La probabilità della somma degli eventi A e B, che sono in comune tra loro, è uguale alla somma delle probabilità dell'evento meno la probabilità del loro lavoro (cioè la loro implementazione congiunta):

R _giunto. (A + B) = P (A) + P (B) - P (AB)

Supponiamo che la probabilità di colpire un bersaglio con un singolo colpo sia 0.4. Quindi evento A - colpire il bersaglio nel primo tentativo, B - nel secondo. Questi eventi sono uniti, perché è possibile che tu possa colpire il bersaglio dal primo e dal secondo colpo. Ma gli eventi non dipendono. Qual è la probabilità del verificarsi di un evento di sconfiggere il bersaglio con due colpi (almeno uno)? Secondo la formula:

0,4 + 0,4-0,4 * 0,4 = 0,64

La risposta alla domanda è: "La probabilità di colpire il bersaglio da due colpi è del 64%."

Questa formula per la probabilità di un evento può essere applicata anche a eventi incompatibili, in cui la probabilità di occorrenza congiunta di un evento P (AB) = 0. Ciò significa che la probabilità della somma di eventi incompatibili può essere considerata un caso speciale della formula proposta.

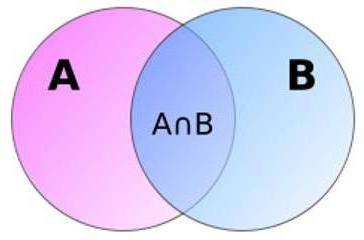
Geometria di probabilità per chiarezza

È interessante notare che la probabilità della somma di eventi congiunti può essere rappresentata nella forma di due regioni A e B, che si intersecano tra loro. Come si può vedere dall'immagine, l'area della loro associazione è uguale all'area totale meno l'area della loro intersezione. Questa spiegazione geometrica rende la formula illogica a prima vista più comprensibile. Si noti che le soluzioni geometriche non sono rare nella teoria della probabilità.

Determinare la probabilità della somma di un insieme (più di due) di eventi congiunti è piuttosto ingombrante. Per calcolarlo, è necessario utilizzare le formule fornite per questi casi.

Eventi dipendenti

Gli eventi dipendenti vengono chiamati se l'occorrenza di uno (A) di essi influenza la probabilità che si verifichi un altro (B). Inoltre, viene presa in considerazione l'influenza sia dell'occorrenza dell'evento A sia della sua non apparizione. Sebbene gli eventi siano chiamati dipendenti per definizione, solo uno di essi dipende (B). La probabilità usuale è indicata come P (B) o la probabilità di eventi indipendenti. Nel caso di dipendenti, viene introdotto un nuovo concetto: la probabilità condizionale P _A (B), che è la probabilità dell'evento dipendente B a condizione che si verifichi un evento A (ipotesi) da cui dipende.

Ma l'evento A è anche accidentale, quindi ha anche una probabilità che deve e può essere presa in considerazione nei calcoli effettuati. Successivamente, un esempio mostrerà come lavorare con eventi dipendenti e un'ipotesi.

Un esempio di calcolo della probabilità di eventi dipendenti

Un buon esempio per il calcolo degli eventi dipendenti può essere un mazzo di carte standard.

Utilizzando l'esempio di un mazzo di 36 carte, consideriamo gli eventi dipendenti. È necessario determinare la probabilità che la seconda carta, estratta dal mazzo, sia del seme dei diamanti, se la prima carta è:

1. I diamanti
2. Un altro vestito.

È ovvio che la probabilità del secondo evento B dipende dalla prima A. Quindi, se la prima opzione è valida, quella nel mazzo era 1 carta (35) e 1 diamante (8) in meno, la probabilità dell'evento B:

P _A (B) = 8/35 = 0,23

Se la seconda opzione è valida, allora ci sono 35 carte nel mazzo, e il numero totale di tamburelli (9) è ancora conservato, quindi la probabilità del prossimo evento B:

Р _A (В) = 9/35 = 0,26.

Si può vedere che se l'evento A è condizionato dal fatto che la prima carta è un tamburello, allora la probabilità dell'evento B diminuisce e viceversa.

Moltiplicazione di eventi dipendenti

Guidato dal capitolo precedente, accettiamo il primo evento (A) come un dato di fatto, ma se parlare in sostanza, è casuale. La probabilità di questo evento, vale a dire l'estrazione di diamanti da un mazzo di carte, è pari a:

P (A) = 9/36 = 1/4

Poiché la teoria non esiste da sola, ma è destinata a servire per scopi pratici, è giusto notare che la probabilità di produrre eventi dipendenti è più spesso necessaria.

Secondo il teorema sul prodotto delle probabilità di eventi dipendenti, la probabilità di occorrenza di eventi congiunti dipendenti A e B è uguale alla probabilità di un evento A moltiplicata per la probabilità condizionale dell'evento B (dipendente da A):

P (AB) = P (A) * P _A (B)

Quindi, nell'esempio con un mazzo, la probabilità di estrarre due carte con un seme di quadri è:

9/36 * 8/35 = 0,0571, o 5,7%

E la probabilità di estrazione all'inizio non è tamburello, e poi tamburelli, è uguale a:

27/36 * 9/35 = 0,19, o 19%

Si può vedere che la probabilità che si verifichi l'evento B è maggiore, a condizione che la carta del seme, diversa dai diamanti, venga prima estratta. Questo risultato è abbastanza logico e comprensibile.

Probabilità totale di un evento

Quando un problema con probabilità condizionali diventa sfaccettato, non può essere calcolato utilizzando metodi convenzionali. Quando ci sono più di due ipotesi, vale a dire A1, A2, ..., A _n , .. forma un gruppo completo di eventi, a condizione che:

• P (A _i )> 0, i = 1,2, ...
• A _i ∩ A _j = Ø, io ≠ j.
• Σ _k A _k = Ω.

Quindi, la formula della probabilità totale per l'evento B con il gruppo completo di eventi casuali A1, A2, ..., A _n è uguale a _:

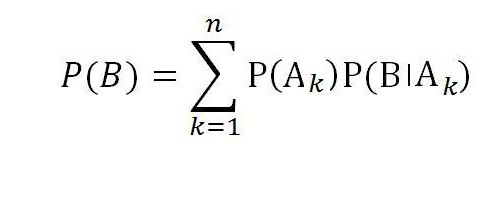
Guardando al futuro

La probabilità di un evento casuale è essenziale in molte aree della scienza: econometria, statistica, fisica, ecc. Poiché alcuni processi non possono essere determinati deterministicamente, poiché sono di natura probabilistica, sono necessari metodi di lavoro speciali. La teoria della probabilità di un evento può essere utilizzata in qualsiasi campo tecnologico come un modo per determinare la possibilità di errore o malfunzionamento.

Possiamo dire che, riconoscendo la probabilità, stiamo in qualche modo facendo un passo teorico verso il futuro, esaminandolo attraverso il prisma delle formule.