Movimento rotazionale e velocità angolare di un solido
In questo articolo discuteremo le grandezze fisiche che caratterizzano il movimento rotatorio del corpo: velocità angolare, spostamento angolare, accelerazione angolare e momento delle forze.
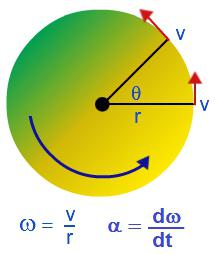
Un corpo rigido è una collezione di punti materiali rigidamente connessi. Quando un corpo solido ruota attorno a qualsiasi asse, i singoli punti materiali da cui è aggiunto si muovono lungo cerchi di raggi diversi.
Per un certo periodo di tempo, per esempio, durante il quale il corpo compie una rivoluzione, i punti materiali separati che costituiscono un corpo solido, passeranno percorsi diversi, quindi, i punti separati avranno diverse velocità lineari. Descrivi la rotazione di un solido usando le velocità lineari dell'individuo punti materiali - difficile.
Ad
Spostamento angolare
Tuttavia, analizzando il movimento dei singoli punti materiali, si può stabilire che nello stesso periodo di tempo girano tutti attorno all'asse con lo stesso angolo. Cioè, per descrivere la rotazione di un solido, è conveniente usare una quantità fisica come lo spostamento angolare:
φ = φ (t).
Velocità angolare e accelerazione angolare
Il movimento rotatorio può essere caratterizzato dalla velocità angolare: ω = Δφ / Δt.
La velocità angolare caratterizza la velocità di rotazione del corpo ed è uguale al rapporto tra la variazione dell'angolo di rotazione e il tempo durante il quale si è verificato. Misurato in radianti al secondo: [ω] = rad / s.
La velocità angolare di rotazione è correlata alla velocità lineare dalla seguente relazione: v = Rω, dove R è il raggio del cerchio lungo il quale si muove il corpo.
Movimento di rotazione il corpo è caratterizzato da un'altra quantità fisica - l'accelerazione angolare, che è uguale al rapporto tra la variazione della velocità angolare e il tempo durante il quale si è verificato: ε = Δω / Δt. L'unità di misura dell'accelerazione angolare: [ε] = rad / s 2 .
Ad
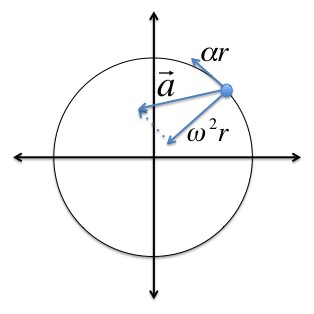
La velocità angolare e l'accelerazione angolare sono pseudovettori, la cui direzione dipende dalla direzione di rotazione. Può essere determinato dalla regola della vite giusta.
Moto rotatorio uniforme
Il movimento rotatorio uniforme viene effettuato con una velocità angolare costante ed è descritto dalle seguenti equazioni: ε = 0, ω = const, φ = φ 0 + ωt, dove φ 0 è il valore iniziale dell'angolo di rotazione.
Moto rotatorio uniformemente accelerato
Il movimento rotatorio uniformemente accelerato avviene con un'accelerazione angolare costante ed è descritto dalle seguenti equazioni: ε = const, ω = ω 0 + εt, φ = φ 0 + ω 0 t + εt 2/2.
Durante la rotazione di un solido accelerazione centripeta ogni punto di questo corpo può essere trovato come segue: ɑ c = v 2 / R = (ωR) 2 / R = ω 2 R.
Quando la rotazione di un solido viene accelerata, puoi trovare l'accelerazione tangenziale dei suoi punti con la formula: ɑ t = Δv / Δt = Δ (ωR) / Δt = R (Δω / Δt) = Rε.
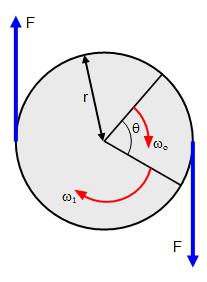
Momento di forza
Se, considerando un problema fisico, non abbiamo a che fare con un punto materiale, ma con un corpo solido, quindi l'azione di diverse forze applicate su diversi punti di questo corpo non può essere ridotta all'azione di una singola forza. In questo caso, considera il momento delle forze.
Ad
Il momento della forza è chiamato il prodotto della forza sulla spalla. Questa è una quantità di vettori e si trova con la formula: M = RFsinα, dove α è l'angolo tra i vettori R e F. Se ci sono diversi momenti di forze che agiscono sul corpo, allora la loro azione può essere sostituita dalla loro risultante somma vettoriale di questi momenti: M = M 1 + M 2 + ... + M n .
Esperimenti ed esperienza dimostrano che sotto l'azione di un momento di forza, la velocità angolare del corpo cambia, cioè il corpo ha accelerazione angolare. Scopriamo come l'accelerazione angolare del punto materiale (insieme di punti materiale) dipende dalla coppia applicata: F = mɑ, RF = Rma = R 2 mβ, β = M / mR 2 = M / I, dove I = mR 2 è il momento di inerzia del materiale punto. Si noti che il momento di inerzia del corpo dipende sia dalla massa del corpo sia dalla posizione di questa massa rispetto all'asse di rotazione.
Esempi di risoluzione dei problemi
Attività 1. Il rotore della centrifuga produce 2 • 10 4 giri / min. Dopo lo spegnimento del motore, la sua rotazione si interrompe dopo 8 minuti. Trova l'accelerazione angolare, nonché il numero di giri effettuati dal rotore dal momento in cui il motore viene spento fino all'arresto, considerando che il movimento del rotore viene accelerato in modo uniforme.
decisione
Cerchiamo di trovare l'accelerazione angolare, tenendo conto che la velocità angolare con moto uniformemente accelerato è descritta dall'equazione: ω (t) = ω 0 - εt.
Quindi, dato che alla fine del movimento la velocità è zero, troviamo: ε = ω 0 / t = 2πn / t.
Trasferendo queste attività sull'unità di unità SI (n = 333 giri / s; t = 480 s) , otteniamo: ε = 2π333 / 480 = 4,3 (rad / s 2 ).
L'angolo di rotazione del rotore della centrifuga durante il tempo t sarà: φ (t) = φ 0 + ω 0 t + εt 2/2. Leggendo l'espressione per l'accelerazione angolare e il fatto che φ 0 = 0 , troviamo: φ (t) = ω 0 t / 2 = πnt.
Ad
Il numero di giri del rotore durante questo tempo sarà: N = φ (t) / 2π = πnt / 2π = nt = 8 • 10 4 (vol.).
Risposta: l'accelerazione angolare è 4,3 rad / s 2 ; il numero di giri effettuati dal rotore dal momento in cui il motore viene spento fino all'arresto completo è 8 • 10 4 giri / min.
Attività 2. Un disco con una massa di 1 kg e un raggio di 20 cm ruota ad una frequenza di 120 giri / min. in un minuto. Sotto l'azione del dispositivo di frenata sul bordo del disco cominciò ad agire forza di attrito 10 N. Trova il tempo di fermare il disco, dopo che ha iniziato ad agire la forza di attrito.
decisione
Trova la coppia frenante che agisce sul disco: M = RF.
Trova l'accelerazione angolare del disco: ε = M / I = FR / mR 2 = F / mR.
Cerchiamo di trovare il tempo per il quale il disco si fermerà: t = ω 0 / ε , dove ω 0 è la velocità angolare iniziale del disco, che è uguale a 2πv.
Facciamo i calcoli: t = 2πv / ε = 2πvmR / F = 6,28 • 2 • 1 • 0,2 / 10 = 2,5 (s).
Risposta: il tempo di arresto è di 2,5 secondi.