Segni di somiglianza di triangoli e la loro applicazione pratica per risolvere i problemi

Nozione di somiglianza arbitraria forme geometriche in sostanza, è molto facile da spiegare e ancor meno da dimostrare. Quindi, ad esempio, guardando un oggetto attraverso una lente d'ingrandimento, vediamo un'immagine di questo oggetto ingrandita più volte con le proporzioni di tutte le sue dimensioni preservate. In altre parole, l'immagine dell'oggetto è simile all'oggetto originale prima dell'ingrandimento. Nella maggior parte dei problemi di geometria, per dimostrare la proporzionalità dei lati e aree triangolari applica i 3 segni principali. Per considerare i segni esistenti della somiglianza dei triangoli, è necessario definire inizialmente il concetto chiave che verrà utilizzato nel testo in futuro.

Quindi, i triangoli sono simili, se i loro lati posizionati in modo simile sono proporzionali, e gli angoli disposti corrispondentemente sono uguali (vale la pena ricordare che i lati sono chiamati simili, o corrispondenti, se si trovano di fronte a angoli identici). Considerare triangoli simili ΔABC e ΔA ₁ B ₁ C ₁ . Secondo il concetto di cui sopra, le parti interessate sono: AB e A ₁ B ₁ , nonché coppie di lati BC e B ₁ C ₁ , AC e A ₁ C ₁ . Si noti che i lati di ciascuna di queste tre coppie giacciono su angoli opposti della stessa ampiezza.

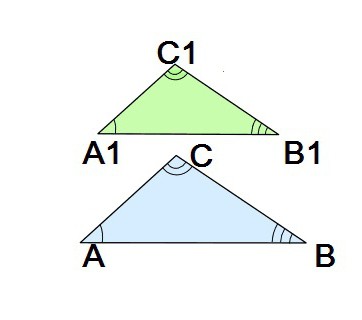La somiglianza è denotata da personaggio speciale che si trova tra le designazioni delle figure in questione: ΔABC ~ Δ A ₁ B ₁ C ₁ .

Il rapporto delle parti rilevanti con la presenza di questa caratteristica è un parametro chiamato coefficiente di somiglianza k. Se k = 2, allora possiamo dire che una delle due figure geometriche considerate è una copia doppia ingrandita dell'altra. È chiaro che se k = 1, allora i triangoli sono uguali. Pertanto, questa uguaglianza può essere considerata un caso speciale della loro somiglianza.

Segni di somiglianza di triangoli

Si scopre che per stabilire la presenza della caratteristica considerata, non è necessario verificare tutti i requisiti elencati nella formulazione della definizione di somiglianza sopra riportata. È sufficiente soddisfare il set minimo di condizioni e lo confermeremo nella pratica.

Primo segno

Quando risolvono i problemi, il primo segno della somiglianza dei triangoli appare in evidenza molto più spesso degli altri. Si noti che funziona con solo due elementi di una figura geometrica: due angoli. I segni rimanenti della somiglianza dei triangoli richiedono la partecipazione di tre elementi. Quindi, per due triangoli simili arbitrari, 2 angoli di uno di essi sono uguali agli stessi 2 angoli dell'altro.

Prova di

In base alle proprietà di base valide per qualsiasi triangolo arbitrario, possiamo scrivere la seguente espressione per ∠C. Il suo valore sarà uguale (180 ° - (∠А + ∠В)), per un altro ∠С _{1 il} valore sarà calcolato secondo lo stesso principio. Per trasformazioni elementari di espressioni, otteniamo che ∠C = C ₁ . Pertanto, tutti gli angoli presenti in ΔАВС sono uguali a tutti gli angoli analoghi situati in ΔА ₁ В ₁ С ₁ . Con un algoritmo simile, i rimanenti segni di somiglianza dei triangoli sono provati.

Secondo segno

Questo approccio alla dimostrazione è spesso usato se gli angoli delle figure geometriche considerate sono noti.

Per due triangoli simili, è vero che i 2 lati di ciascuno di essi sono proporzionali ai secondi lati simili dell'altro, e gli angoli tra queste coppie di lati sono uguali.

Prova di

Per provare questa funzione, è necessario fare riferimento ai calcoli precedenti. Sulla base dei risultati sopra, è sufficiente dimostrare che ∠В = В ₁ . Considerare ΔABC ₂ , per il quale, secondo il primo segno, le seguenti affermazioni sono vere: ∠1 = ∠А ₁ , ∠2 = В ₁ . ΔABC ₂ ~ ΔА ₁ В ₁ С ₁ . Ciò significa AB / A ₁ B ₁ = AC ₂ / A ₁ C. D'altra parte, è noto dalla condizione che sussiste la seguente relazione: AC / A ₁ C _{1 =} AB / A ₁ B ₁ . Di conseguenza, otteniamo l'uguaglianza dei lati AC = AC ₂ , così come l'affermazione che ΔABC ~ ΔABC ₂ secondo il secondo segno (AC = AC ₂ e ∠A = ∠1, poiché, come risultato dei dati iniziali, è stato stabilito che A = ∠ A ₁ e ∠1 = ∠ A ₁ , AB- è un lato comune per questi due triangoli). Dalla dimostrazione risulta che ∠B = ∠2, e poiché ∠2 = ∠В ₁ , otteniamo che ∠В = В ₁ . Da ciò segue che viene dimostrato un altro segno.

Terzo segno

Questa caratteristica è considerata la più ovvia quando si prova la somiglianza, poiché vengono considerati tutti i lati di questi triangoli con parametri noti.

Quindi, per due triangoli che sono simili tra loro, vi è una dichiarazione che 3 lati di uno di essi sono proporzionali a 3 lati corrispondenti dell'altro.

Prova di

Considerando la precedente caratteristica di similarità, ora per costruire una dimostrazione basta stabilire che esiste un'eguaglianza della forma: ∠A = ∠A ₁ . Per fare ciò, considera qualsiasi ΔABC ₂ arbitrario, per il quale ∠1 = ∠ A ₁ , 2 = В ₁ . Secondo il primo attributo ΔABC ₂ ~ ΔA ₁ B ₁ C ₁ , quindi per questi due triangoli possiamo scrivere il rapporto del tipo AB / A ₁ B ₁ = BC ₂ / B ₁ C ₁ = C ₂ A / C ₁ A _1, da cui possiamo scrivere l'uguaglianza della forma: B ₁ C ₁ = BC ₂ , A ₁ C ₁ = AC ₂ . Da questo è logico concludere che ΔABC ~ ΔABC _2, e, in conclusione, ∠A e ∠A ₁ sono uguali. Da ciò segue che anche la caratteristica considerata è dimostrata.

proprietà

1. Per due triangoli, simili tra loro, il rapporto tra i valori delle loro aree è direttamente proporzionale al coefficiente al quadrato. Proof. Considera due figure arbitrarie con tre lati e tre angoli simili tra loro. Sia A e A ₁ siano i lati corrispondenti di queste figure, e h e h ₁ siano le altezze corrispondenti. Sia k il coefficiente di somiglianza per i triangoli considerati, quindi, dal rapporto d'aspetto possiamo scrivere un'equazione della forma: A ₁ = k * A. È facile vedere che per il rapporto altezza possiamo scrivere un'equazione della forma: h ₁ = k * h. Per il rapporto tra le aree delle figure geometriche considerate, otteniamo: S ₁ / S = (1 / 2a ₁ h ₁ ) / (1 / 2ah) = (a ₁ / a) * (h ₁ / h) = k * k = k ² . Pertanto, quando un triangolo viene "allungato" di 2 volte, la sua area aumenta di 2 ² = 4 volte. La seconda proprietà deriva dalla prova precedente ed è direttamente correlata ad essa.
2. Tutte le linee corrispondenti tracciate in tali triangoli sono anche proporzionali tra loro e pari al valore del coefficiente rivelato sopra. Cioè, secondo la proprietà di cui sopra, si può sostenere che tutte le costruzioni addizionali interne saranno anche proporzionali.

Aggiunta alla lista principale dei segni

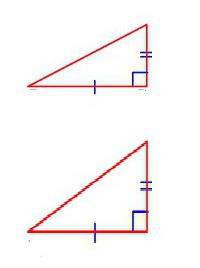
Vale la pena prendere in considerazione un numero di caratteristiche individuali applicabili alle forme geometriche di un certo tipo. Quindi i triangoli rettangoli sono simili se:

• la loro ipotenusa e ognuna delle due gambe sono rispettivamente proporzionali;
• se i loro corrispondenti angoli acuti sono uguali;
• se tutte le gambe dei triangoli considerati sono proporzionali alla coppia.

conclusione

Quindi, abbiamo combinato tutti i possibili segni, con l'aiuto di cui si può in qualche modo dimostrare la somiglianza di due o più figure con tre angoli e lati, indipendentemente dal loro tipo e proprietà. Nella maggior parte dei problemi di geometria, i tre segni principali sono utilizzati per dimostrare la proporzionalità dei lati e delle aree, ma non abbiamo trascurato un numero di segni di somiglianza che sono applicabili solo se è necessario eseguire la prova per le figure geometriche in questione con un angolo retto. Questi segni di somiglianza triangoli rettangoli semplifica enormemente il processo di risoluzione di vari tipi di attività e richiede un minimo di dati per loro.