Alcuni punti su come viene eseguita la soluzione delle disuguaglianze
Uno degli argomenti che richiede la massima attenzione e perseveranza da parte degli studenti è la soluzione delle disuguaglianze. Tale simile alle equazioni e allo stesso tempo molto diverso da loro. Perché la loro soluzione richiede un approccio speciale.
Proprietà che saranno richieste per trovare la risposta
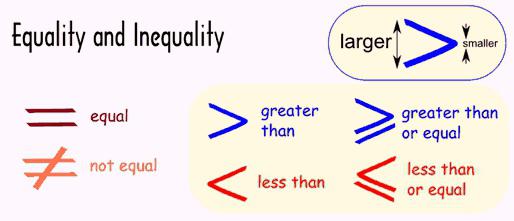
Tutti loro sono usati per sostituire il record esistente con un equivalente. Molti di loro sono simili a quello che c'era nelle equazioni. Ma ci sono differenze.
- Una funzione definita nell'LDU o qualsiasi numero può essere aggiunta a entrambi i lati della disuguaglianza originale.
- Allo stesso modo, la moltiplicazione è possibile, ma solo da una funzione o un numero positivo.
- Se questa azione viene eseguita con una funzione o un numero negativo, il segno di disuguaglianza deve essere sostituito con quello opposto.
- Le funzioni non negative possono essere aumentate a potenza positiva.
A volte la soluzione delle disuguaglianze è accompagnata da azioni che danno risposte estranee. Devono essere eliminati confrontando il dominio del DHS e una varietà di soluzioni.
Utilizzando il metodo di spaziatura
La sua essenza è ridurre la disuguaglianza all'equazione, in cui nella parte destra è zero.
- Determina l'area in cui si trovano i valori validi delle variabili, cioè l'LDL.
- Trasforma la disuguaglianza con l'aiuto delle operazioni matematiche in modo che nella sua parte destra ci sia uno zero.
- Sostituisci il segno di disuguaglianza con "=" e risolvi l'equazione corrispondente.
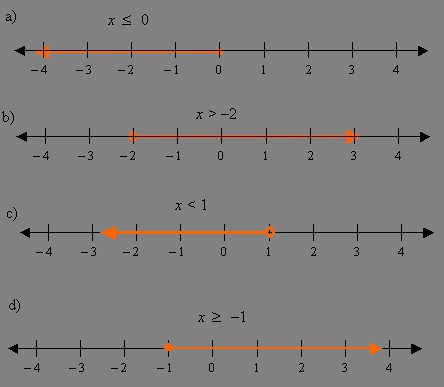
- Sull'asse numerico, segnare tutte le risposte che si sono verificate durante la soluzione, nonché gli intervalli TLD. Con una rigorosa disuguaglianza del punto devi disegnare forato. Se c'è un segno di uguale, allora dovrebbero dipingere.
- Determina il segno della funzione originale su ciascun intervallo risultante dai punti dell'LDD e dividendo le sue risposte. Se alla transizione attraverso il punto il segno della funzione non cambia, allora entra nella risposta. Altrimenti - escluso.
- I punti di confine per i TLD devono essere ulteriormente controllati e solo allora inclusi o meno nella risposta.
- La risposta, che si ottiene, deve essere scritta sotto forma di serie unite.
Poco sulle doppie diseguaglianze
Usano due segni di disuguaglianza nel record. Cioè, alcune funzioni sono limitate dalle condizioni immediatamente due volte. Tali diseguaglianze sono risolte, come un sistema di due, quando l'originale è diviso in parti. E nel metodo dell'intervallo sono indicate le risposte dalla soluzione di entrambe le equazioni.
Ad
Per risolverli, è anche consentito utilizzare le proprietà sopra specificate. Con il loro aiuto, è conveniente ridurre la disuguaglianza all'uguaglianza zero.

Qual è la situazione delle disuguaglianze in cui esiste un modulo?
In questo caso, la soluzione delle disuguaglianze utilizza le seguenti proprietà e sono vere per un valore positivo di "a".
Se "x" assume un'espressione algebrica, allora tali sostituzioni sono vere:
- | x | <a to -a <x <a;
- | x | > a su x <-a o x> a.
Se le diseguaglianze non sono rigide, allora anche le formule sono vere, solo in esse, ad eccezione del segno più o meno, appare "=".
Come risolvere un sistema di disuguaglianze?
Questa conoscenza sarà richiesta nei casi in cui tale compito è dato o vi è un record di doppia disuguaglianza o un modulo appare nel record. In una tale situazione, la soluzione sarebbe valori di variabili che soddisferebbero tutte le disuguaglianze nel record. Se non ci sono tali numeri, il sistema non ha soluzioni.
Ad
Il piano per la soluzione del sistema di disuguaglianze:
- risolvi ciascuno di loro separatamente;
- disegna tutti gli intervalli sull'asse numerico e determina le loro intersezioni;
- scrivi la risposta del sistema, che sarà l'unione di quanto accaduto nel secondo paragrafo.
Come affrontare le disuguaglianze frazionarie?
Poiché durante la loro soluzione potrebbe essere necessario modificare il segno di disuguaglianza, è necessario eseguire tutti i punti del piano con molta attenzione e attenzione. Altrimenti, potrebbe essere la risposta opposta.
La soluzione delle disuguaglianze frazionali utilizza anche il metodo dell'intervallo. E il piano d'azione sarà:
- Usando le proprietà descritte, dare alla frazione un aspetto tale che solo zero rimane a destra del segno.
- Sostituisci la disuguaglianza con "=" e determina i punti in cui la funzione sarà uguale a zero.
- Contrassegnali sull'asse delle coordinate. In questo caso, i numeri risultanti dai calcoli del denominatore saranno sempre perforati. Tutti gli altri - in base alle condizioni di disuguaglianza.
- Determina gli intervalli di consistenza.
- In risposta, scrivi l'unione di quegli intervalli, il cui segno corrisponde a quello che era nella disuguaglianza originale.
Situazioni in cui l'irrazionalità appare nella disuguaglianza
In altre parole, c'è una radice matematica nel record. Dal momento che nel corso di algebra della scuola la maggior parte dei compiti va avanti radice quadrata allora sarà considerato.
La soluzione delle disuguaglianze irrazionali è quella di ottenere un sistema di due o tre, che sarà equivalente all'originale.
| Disuguaglianza originale | condizione | sistema equivalente |
| √ n (x) <m (x) | m (x) è minore o uguale a 0 | nessuna soluzione |
| m (x) maggiore di 0 | n (x) è maggiore o uguale a 0 n (x) <(m (x)) 2 | |
| √ n (x)> m (x) | m (x) è maggiore o uguale a 0 n (x)> (m (x)) 2 | |
o n (x) è maggiore o uguale a 0 m (x) è minore di 0 | ||
| √n (x) ≤ m (x) | m (x) è minore di 0 | nessuna soluzione |
| m (x) è maggiore o uguale a 0 | n (x) è maggiore o uguale a 0 n (x) ≤ (m (x)) 2 | |
| √n (x) ≥ m (x) | m (x) è maggiore o uguale a 0 n (x) ≥ (m (x)) 2 | |
o n (x) è maggiore o uguale a 0 m (x) è minore di 0 | ||
| √ n (x) <√ m (x) | n (x) è maggiore o uguale a 0 n (x) è minore di m (x) | |
| √n (x) * m (x) <0 | n (x) è maggiore di 0 m (x) è minore di 0 | |
| √n (x) * m (x)> 0 | n (x) è maggiore di 0 m (x) maggiore di 0 | |
| √n (x) * m (x) ≤ 0 | n (x) è maggiore di 0 m (x) ≤0 | |
o n (x) è 0 m (x) - qualsiasi | ||
| √n (x) * m (x) ≥ 0 | n (x) è maggiore di 0 m (x) ≥0 | |
o n (x) è 0 m (x) - qualsiasi |
Esempi di risoluzione di diversi tipi di disuguaglianze
Per aggiungere chiarezza alla teoria della soluzione delle disuguaglianze, di seguito sono riportati alcuni esempi.
Primo esempio 2x - 4> 1 + x
Soluzione: per determinare il TLD, è sufficiente osservare da vicino la disuguaglianza. È formato da funzioni lineari, quindi è definito per tutti i valori della variabile.
Ora da entrambi i lati della disuguaglianza si deve sottrarre (1 + x). Risulta: 2x - 4 - (1 + x)> 0. Dopo che le parentesi sono state aperte e tali termini sono stati assegnati, la disuguaglianza assume la forma seguente: x - 5> 0.
Ad
Paragonandolo a zero, è facile trovare la sua soluzione: x = 5.
Ora questo punto con il numero 5, è necessario segnare sul fascio di coordinate. Quindi controlla i segni della funzione originale. Nel primo intervallo da meno infinito a 5, puoi prendere il numero 0 e sostituirlo nella disuguaglianza risultante dalle trasformazioni. Dopo i calcoli, risulta -7> 0. sotto l'arco dell'intervallo devi firmare un segno meno.
Nell'intervallo successivo, da 5 a infinito, puoi scegliere il numero 6. Quindi risulta che 1> 0. Sotto l'arco, il segno "+" è firmato. Questo secondo intervallo sarà la risposta alla disuguaglianza.
Risposta: x giace nell'intervallo (5; ∞).
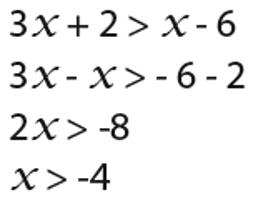
Il secondo esempio. È necessario risolvere un sistema di due equazioni: 3x + 3 ≤ 2x + 1 e 3x - 2 ≤ 4x + 2.
La decisione L'LDL di queste disuguaglianze si trova anche nel dominio di qualsiasi numero, poiché vengono fornite funzioni lineari.
Quindi è necessario agire in fasi. In primo luogo converti la prima delle disuguaglianze e rendila uguale a zero. 3x + 3 - 2x - 1 = 0. Cioè, x + 2 = 0. Quindi, x è -2.
La seconda disuguaglianza assumerà la forma di una simile equazione: 3x - 2 - 4x - 2 = 0. Dopo la trasformazione: -x - 4 = 0. Produce un valore per la variabile pari a -4.
Questi due numeri dovrebbero essere segnati sull'asse, raffiguranti gli intervalli. Poiché la disuguaglianza non è rigida, tutti i punti devono essere dipinti. Il primo intervallo da meno infinito a -4. Lascia che il numero sia -5. La prima diseguaglianza darà un valore di -3, e il secondo 1. Pertanto, questa lacuna non entra nella risposta.
Ad
Il secondo intervallo va da -4 a -2. Puoi scegliere il numero -3 e sostituirlo in entrambe le disuguaglianze. Nel primo e nel secondo, si ottiene il valore -1. Quindi, sotto l'arco "-".
Nell'ultimo intervallo da -2 a infinito, il numero migliore è zero. È necessario sostituirlo e trovare i valori delle disuguaglianze. Nel primo di essi viene ottenuto un numero positivo e il secondo è zero. Anche questo divario dovrebbe essere escluso dalla risposta.
Dei tre intervalli, la soluzione alla disuguaglianza è solo uno.
Risposta: x appartiene a [-4; -2].

Il terzo esempio. | 1 - x | > 2 | x - 1 |.
La decisione Il primo passo è determinare i punti in cui le funzioni spariscono. Per la sinistra questo numero sarà 2, per quello giusto - 1. dovrebbero essere marcati sul raggio e determinare gli intervalli del segno di costanza.
Ad
Nel primo intervallo, da meno infinito a 1, la funzione dal lato sinistro della disuguaglianza assume valori positivi, e dal lato destro assume valori negativi. Sotto l'arco, è necessario annotare i due caratteri "+" e "-" fianco a fianco.
L'intervallo successivo è da 1 a 2. Su di esso, entrambe le funzioni assumono valori positivi. Quindi, sotto l'arco, due più.
Il terzo intervallo da 2 a infinito dà il seguente risultato: la funzione sinistra è negativa, quella destra è positiva.
Tenendo conto dei segni risultanti, è necessario calcolare i valori di disuguaglianza per tutti gli intervalli.
Sulla prima, otteniamo la seguente disuguaglianza: 2 - x> - 2 (x - 1). Il meno prima dei due nella seconda disuguaglianza è dovuto al fatto che questa funzione è negativa.
Dopo la trasformazione, la disuguaglianza si presenta come segue: x> 0. Fornisce immediatamente i valori della variabile. Cioè, da questo intervallo tornerà solo l'intervallo da 0 a 1.
Sul secondo: 2 - x> 2 (x - 1). Le conversioni daranno la seguente disuguaglianza: -3x + 4 più di zero. Il suo zero è x = 4/3. Tenendo conto del segno di disuguaglianza, risulta che x deve essere inferiore a questo numero. Quindi, questo intervallo è ridotto all'intervallo da 1 a 4/3.
Quest'ultimo fornisce il seguente record di disuguaglianza: - (2 - x)> 2 (x - 1). La sua trasformazione porta a quanto segue: x> 0. Cioè, l'equazione è vera per x inferiore a zero. Ciò significa che nella disuguaglianza del divario richiesto non fornisce soluzioni.
Nei primi due intervalli, il confine si è rivelato essere il numero 1. Deve essere controllato separatamente. Cioè, sostituisci la disuguaglianza originale. Risulta: | 2 - 1 | > 2 | 1 - 1 |. Il calcolo indica che 1 è maggiore di 0. Questa è un'istruzione valida, quindi è inclusa nella risposta.
Risposta: x giace nell'intervallo (0; 4/3).