La bisettrice di un triangolo - che cos'è?

La geometria è una delle scienze più complesse e complesse. In esso, ciò che sembra ovvio a prima vista molto raramente risulta corretto. Bisettrici, altezze, mediane, proiezioni, tangenti sono un numero enorme di termini veramente difficili con cui è facile confondersi.

Infatti, con il giusto desiderio, puoi comprendere la teoria di qualsiasi complessità. Quando si parla di bisettrice, mediana e altezza, è necessario capire che non sono peculiari dei triangoli. A prima vista, si tratta di linee semplici, ma ognuna ha le sue proprietà e funzioni, la cui conoscenza semplifica enormemente la soluzione dei problemi geometrici. Allora, qual è la bisettrice di un triangolo?

definizione

Il termine "bisettrice" deriva da una combinazione delle parole latine "due" e "taglia", "taglia", che indicano indirettamente le sue proprietà. Di solito, quando i bambini vengono introdotti a questa trave, viene loro chiesto di memorizzare una breve frase: "La bisettrice è un topo che corre negli angoli e dimezza l'angolo". Naturalmente, una spiegazione del genere non è adatta per gli studenti più grandi, inoltre, di solito vengono loro chiesti non sul carbone, ma su forma geometrica. Quindi la bisettrice di un triangolo è un raggio che collega il vertice del triangolo con il lato opposto, dividendo l'angolo in due parti uguali. Il punto del lato opposto, a cui arriva la bisettrice, perché un triangolo arbitrario viene scelto casualmente.

Funzioni e proprietà di base

Le proprietà principali di questo raggio un po '. Primo, perché la bisettrice di un triangolo divide l'angolo a metà, qualsiasi punto giacente su di esso sarà ad uguale distanza dai lati che formano il vertice. In secondo luogo, in ogni triangolo si possono disegnare tre bisettrici, in base al numero di angoli disponibili (quindi, ce ne saranno già quattro nello stesso quadrilatero, e così via). Il punto in cui tutti e tre i raggi si intersecano è il centro di un cerchio inscritto in un triangolo.

Le proprietà sono complicate

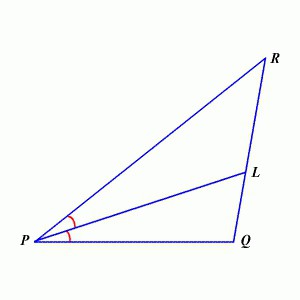
Facciamo un po 'più complicata la teoria. Un'altra proprietà interessante: la bisettrice dell'angolo di un triangolo divide il lato opposto in segmenti il ​​cui rapporto è uguale al rapporto tra i lati che formano il vertice. A prima vista, questo è difficile, ma in realtà tutto è semplice: nella figura proposta, RL: LQ = PR: PK. A proposito, questa proprietà fu chiamata il Teorema su Bisectrix e apparve per la prima volta nelle opere dell'antico matematico greco Euclide. L'hanno ricordato in uno dei libri di testo russi solo nel primo quarto del diciassettesimo secolo.

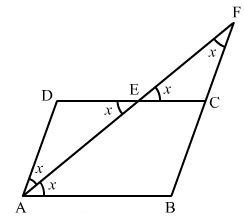
Un po 'più difficile. Nel quadrilatero la bisettrice taglia un triangolo isoscele. Questa figura mostra tutti gli angoli uguali per l'AF mediana.

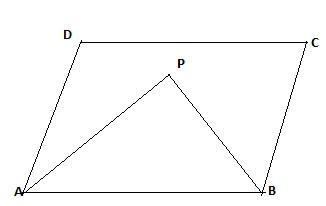
Inoltre, nei quadrangoli e trapezi, le bisettrici di angoli unilaterali sono perpendicolari tra loro. Nel disegno, l'angolo dell'APP è di 90 gradi.

In un triangolo isoscele

L'isoscele di un triangolo isoscele è un raggio molto più utile. È allo stesso tempo non solo un divisore di un angolo a metà, ma anche una mediana e un'altezza.

Una mediana è un segmento che esce da un certo angolo e cade al centro del lato opposto, dividendolo in parti uguali. L'altezza è una perpendicolare caduta da un vertice al lato opposto, con il suo aiuto qualsiasi compito può essere ridotto al teorema di Pitagora semplice e primitivo. In questa situazione, la bisettrice del triangolo è uguale alla radice della differenza tra il quadrato dell'ipotenusa e l'altra gamba. A proposito, è questa proprietà che si trova più spesso nei problemi geometrici.

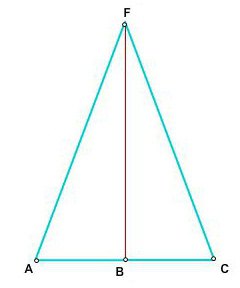
Per risolvere il problema: in questo triangolo, la bisettrice FB è la mediana (AB = BC) e l'altezza (gli angoli di FBC e FBA sono 90 gradi).

In termini generali

Quindi, cosa hai bisogno di ricordare? Una bisettrice triangolare è un raggio che divide la sua metà superiore. All'intersezione dei tre raggi si trova il centro del cerchio inscritto in questo triangolo (l'unico svantaggio di questa proprietà è che non ha valore pratico e serve solo per la corretta esecuzione del disegno). Divide anche il lato opposto in segmenti, il cui rapporto è uguale al rapporto tra i lati tra cui è passato questo raggio. In un quadrilatero, le proprietà sono leggermente più complicate, ma, per ammetterlo, praticamente non si verificano nelle attività a livello di scuola, e quindi di solito non sono influenzate dal programma.

La bisettrice di un triangolo isoscele è il sogno ultimo di ogni studente. È allo stesso tempo una mediana (cioè divide il lato opposto a metà) e l'altezza (perpendicolare a questo lato). La risoluzione dei problemi con una tale bisettrice è ridotta al teorema di Pitagora.

La conoscenza delle funzioni di base della bisettrice, così come le sue proprietà di base, è necessaria per risolvere problemi geometrici di medio e alto livello di complessità. In realtà, questo raggio si trova solo in planimetria, quindi è impossibile dire che memorizzare le informazioni su di esso permetterà di far fronte a tutti i tipi di compiti.