Il concetto del momento angolare, la sua legge di conservazione e un esempio di risoluzione del problema
Il movimento rotazionale non è meno comune in natura del movimento lineare degli oggetti. Per verificare ciò, è sufficiente ricordare la rotazione delle ruote delle auto e delle biciclette, le pale degli elicotteri e dei fan, i pianeti attorno al proprio asse e attorno alle sue stelle. Per descrivere il processo di movimento circolare degli oggetti, viene utilizzata una quantità fisica, che è chiamata "momento angolare". Considera nell'articolo cos'è.
Momento di moto della particella e asse di rotazione
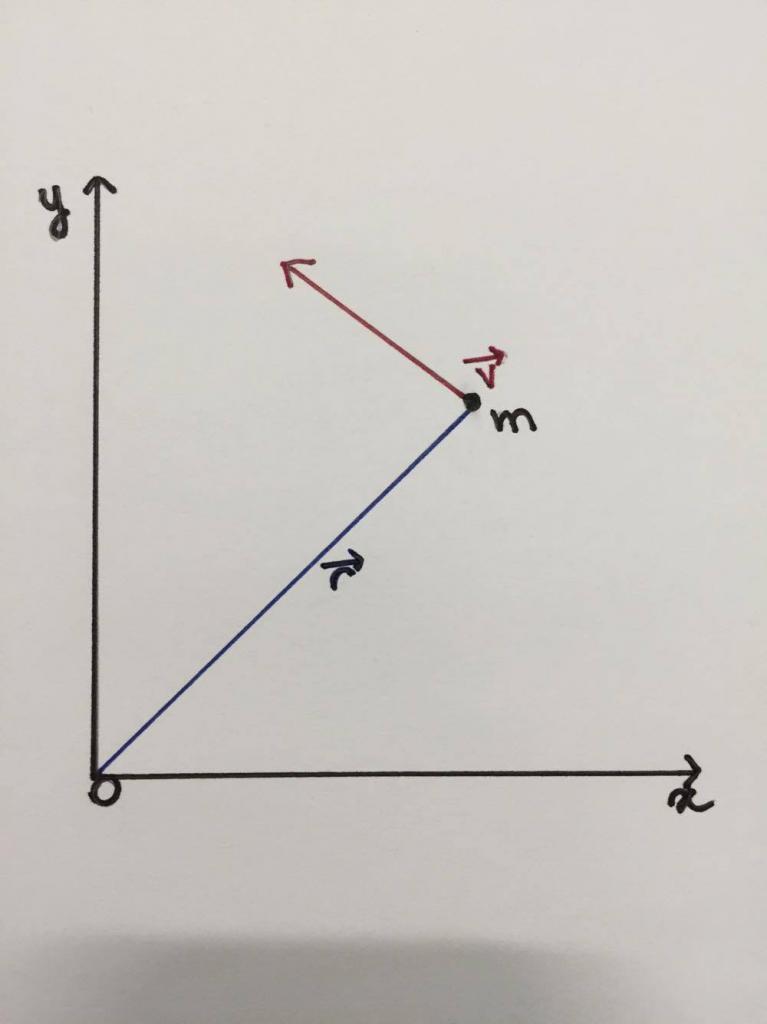
Di seguito un disegno che mostra schematicamente che una particella o un punto materiale di massa m si muove lungo una traiettoria circolare di raggio ¯ con una velocità ν diretta tangenzialmente. L'asse di rotazione è perpendicolare al piano della figura nel punto O.
Ad
Introduciamo la seguente quantità fisica:
L¯ = r¯ * m * v¯ = r¯ * p¯.
Si chiama momento angolare o momento angolare. Come puoi vedere, questa è una quantità di vettori. La sua direzione può essere determinata dalla regola della mano destra: devi dirigere 4 dita in modo che, muovendosi lungo il vettore r¯, giungano alla fine del vettore p¯ (o v¯), quindi il pollice mostrerà la direzione L¯. In questo caso, L¯ è diretto al lettore perpendicolare al piano di disegno.
Poiché la velocità delle particelle (quantità di moto) nella figura è diretta ad angolo retto rispetto al vettore ¯, l'equazione ridotta può essere riscritta in forma scalare:
L = r * m * v = r * p.
Velocità angolare e momento di inerzia
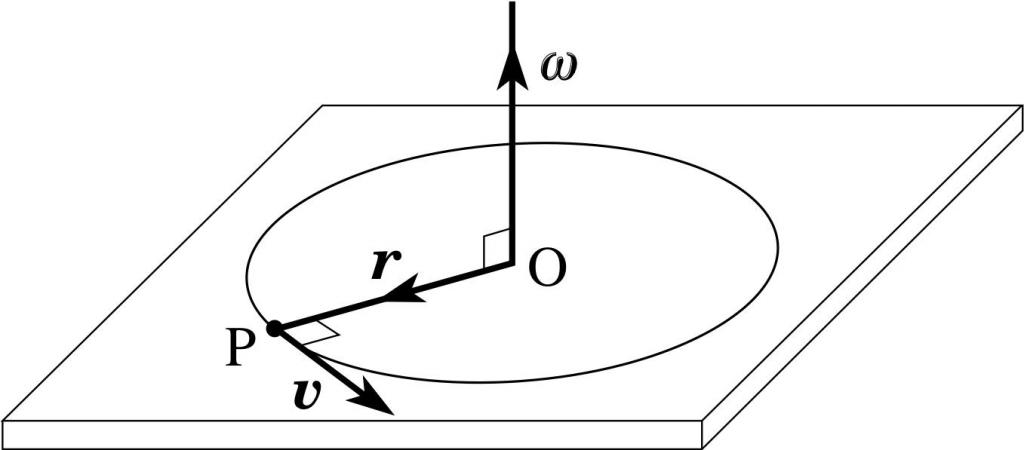
La quantità di moto di una particella dell'esempio precedente può essere scritta attraverso la velocità angolare ω. Per fare ciò, usiamo la sua connessione con la velocità lineare:
ω = v / r => v = ω * r.
Sostituendo l'ultima equazione in un'equazione scalare per L, otteniamo:
L = r 2 * m * ω = I * ω, dove I = r 2 * m.
Qui sono il momento di inerzia della particella. L'espressione risultante viene spesso utilizzata per risolvere problemi pratici, uno dei quali verrà discusso di seguito.
La legge di conservazione del moto rotatorio

Il movimento in un cerchio, così come il movimento lineare degli oggetti nello spazio, è caratterizzato da leggi di conservazione. Uno di questi è la conservazione del momento angolare. Abbiamo questa legge.
L'equazione del tipo di movimento considerato ha la seguente forma:
dL / dt = M.
Dove dL / dt caratterizza il cambiamento nel momento angolare di un corpo nel tempo, quando è influenzato da un certo momento M creato da forze esterne (non interne). Se questo momento di forza è zero, allora il lato sinistro dell'espressione svanisce, il che significa L = const. Per questo caso, possiamo scrivere la seguente uguaglianza:
Ad
L = const = I 1 * ω 1 = I 2 * ω 2 .
Cosa significa questo disco? Si dice che se un corpo ruotasse con velocità ω 1 e avesse un momento di inerzia I 1 , allora a causa di alcune forze interne (non esterne) il momento di inerzia cambiò e divenne uguale a I 2 , allora la nuova velocità di rotazione ω 2 sarà proporzionale associato a questo cambiamento.
La relazione registrata è chiamata la legge di conservazione del momento angolare di un punto (corpo) per analogia con la legge corrispondente per le quantità lineari (conservazione del momento), poiché il momento di inerzia gioca il ruolo della massa, e il valore angolare ω gioca il ruolo della massa.
Usando la legge L = const
La relazione considerata nel paragrafo precedente può essere vista in azione quando eseguono pattinatori o ballerine. Eseguendo acrobazie complesse, ruotano i loro corpi, disperdendo le loro braccia e gambe, e quindi premono le loro membra contro il corpo. L'ultima azione porta ad una diminuzione del valore di I e, di conseguenza, ad un aumento della velocità di rotazione, che crea un effetto piuttosto spettacolare.
Ad

Un altro esempio dell'uso dell'immutabilità del momento angolare di un sistema è l'implementazione della rotazione di un satellite artificiale nello spazio. Per fare ciò, esegui un volano speciale ad esso collegato. Poiché il momento angolare totale non deve cambiare a causa dell'azione delle forze interne, il satellite stesso inizia a ruotare nella direzione opposta. Non appena si gira verso l'angolo desiderato attorno al suo asse, il volano viene fermato con l'aiuto di un motore elettrico, e il corpo satellite ferma anche la sua rotazione.
Calcola il momento di inerzia
Poiché il valore di I è presente nella legge di conservazione del moto circolare, dovremmo dire alcune parole a riguardo. Caratterizza l'inerzia del sistema, cioè quanto "difficile" o "facile" scatenare. Ad esempio, il volano di un'auto ha una grande massa e un raggio relativamente grande, quindi il suo momento di inerzia è significativo. Al contrario, la ruota della bicicletta è fatta di un cerchio leggero in alluminio, quindi per questo sarò relativamente piccola.
Ad
Per calcolare questa caratteristica fisica, utilizzare la formula:
I = ∫ m (r 2 * dm).
Da ciò si vede che il momento di inerzia è una caratteristica del sistema in cui entra il corpo della rivoluzione, e non il corpo stesso. Questo fatto distingue I dall'inerzia lineare, che dipende esclusivamente dalle proprietà del corpo (la sua massa).
Compito con un'asta rotante
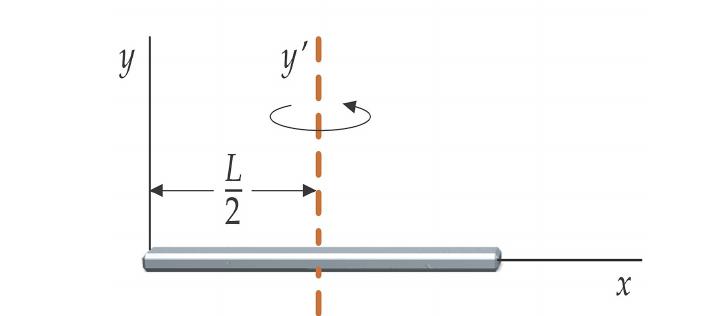
Risolveremo un problema interessante: c'è una barra solida che ruota intorno a un asse situato alla sua estremità. Se questo asse viene spostato dolcemente al centro di massa dell'asta, come cambierà la sua velocità di rotazione?
Questo è un compito classico per applicare la legge di conservazione del momento angolare. La difficoltà sta nel calcolare il cambiamento nel momento di inerzia. Per fare ciò, è possibile utilizzare la formula precedente con un integrale, ma sarà più semplice osservare i valori necessari di I nella letteratura di riferimento.
All'inizio, l'asse di rotazione passava attraverso l'estremità dell'asta. Per questo sistema, il momento di inerzia è pari a:
I 1 = m * L 2/3, dove L è la lunghezza dell'asta, m è la sua massa.
Quando l'asse è stato spostato al centro di massa dell'oggetto, il suo momento di inerzia è cambiato, è diventato uguale a:
I 2 = m * L 2/12.
Applicare la legge di conservazione per L, otteniamo:
m * L 2/3 * ω 1 = m * L 2/12 * ω 2 => ω 2 / ω 1 = m * L 2/3 / (m * L 2/12) = 4.
Abbiamo ricevuto una risposta al problema: l'asta ruoterà 4 volte più velocemente rispetto all'inizio.