Il concetto di matrice e definizioni di base

Un tale concetto come una matrice viene usato e appare nelle sezioni della matematica superiore. Molto spesso si trova nel sistema di equazioni lineari. Allora, qual è il concetto di base di una matrice? Per capire questo, non è necessario essere un genio matematico.

Una matrice è qualcosa che è un sistema di numeri mn, che in matematica sono scritti sotto forma di tabelle, in cui m sono le righe e n sono le colonne. Al suo incrocio ci sono elementi. La dimensione della matrice dipende dal numero di righe e colonne.

Inizialmente, è stata considerata una matrice triangolare, ma non è conveniente per risolvere equazioni complesse, pertanto in matematica viene utilizzato un analogo rettangolare. Un tale sistema è considerato conveniente per risolvere il problema.

Da dove viene la matrice

Se parliamo della prima menzione, il concetto di matrice è venuto dalla Cina, o meglio è stato associato a "quadrati magici". Queste tabelle erano considerate amuleti a causa dei numeri inscritti su di loro. A quel tempo non c'era né il concetto stesso di matrice, né i modi per risolverlo. In alcune tribù stabilì il grado di parentela in modo che le persone scoprissero se potevano sposarsi o meno.

Ma il concetto stesso fu introdotto all'inizio del XIX secolo da James Sylvester, che era un matematico inglese. Vari scienziati hanno lavorato sulla teoria delle matrici, creando un complesso di soluzioni per problemi algebrici difficili.

Matrix e i suoi principali tipi

Quindi, prima era considerato il concetto di una matrice. I tipi di matrici sono presentati di seguito:

• Minuscole. Consiste di una singola riga, ovvero, questo tipo di matrice ha il numero di righe esattamente m = 1, ma il numero delle sue colonne è arbitrario.
• Una colonna. Questa varietà consiste di una sola colonna, ma può contenere anche più righe. Per questo tipo di matrice ha una sua entrata universale. Indica che gli elementi tra parentesi dovrebbero essere scritti come una colonna. Oltre a ciò, risparmia non solo lo spazio, ma anche il tempo.
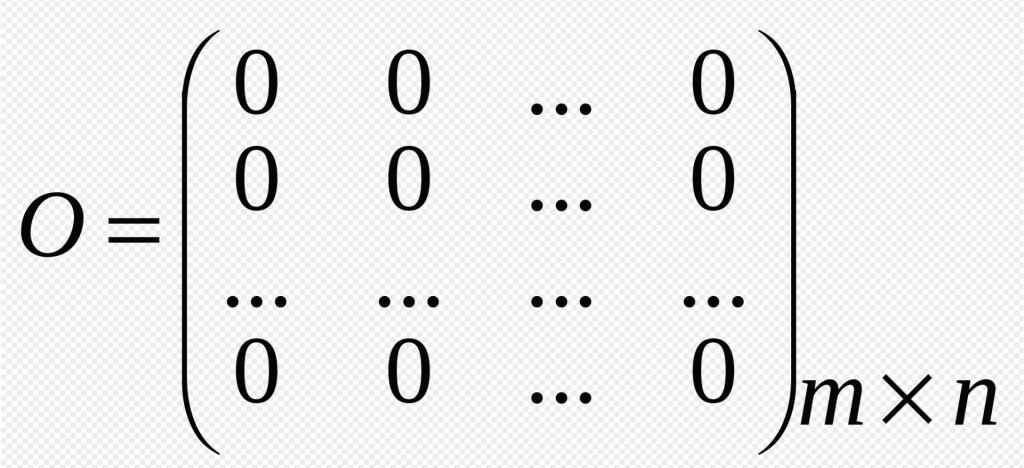
• Matrice Null Questa forma esiste quando tutti i suoi elementi sono uguali a 0. Denotano questo tipo di matrice "O" Questo elemento ha anche ricevuto il suo nome dovuto al fatto che nel calcolo ha funzioni simili con zero nella teoria dei numeri.
• Square. Questo tipo di matrice è il più comune, la sua differenza sta nel fatto che ha un numero uguale di colonne e righe. Quando due elementi sono collegati alle estremità diverse della colonna, otteniamo la diagonale principale. A questo proposito, la tabella diagonale è divisa in diversi sistemi:

a) Diagonale. Questo tipo di matrice quadrata, che non include gli elementi appartenenti alla diagonale principale.

b) Singolo. Questo tipo di diagonale consiste di una sola unità. Per tutto questo, ciascuna di queste matrici è scalare.

c) Scalare. Questo è il tipo in cui la diagonale principale è composta dallo stesso numero.

d) Freccia. Questo è un tipo di matrice quadrata in cui quasi tutti gli elementi sono zero, ma i componenti che compongono la prima colonna, così come quelli relativi alla diagonale e alla prima riga, non sono uguali ad esso.

• Binary. Questo tipo di tabella è composto da zero e uno.
• Matrice di Pascal - in questo tipo di matrice tutti gli elementi sono costituiti da numeri appartenenti al triangolo con lo stesso nome.
• Tridiagonali. In questo tipo di matrice, gli elementi non nulli si trovano su tre diagonali, che includono quello principale e quelli sopra e sotto.

Matrice di rango

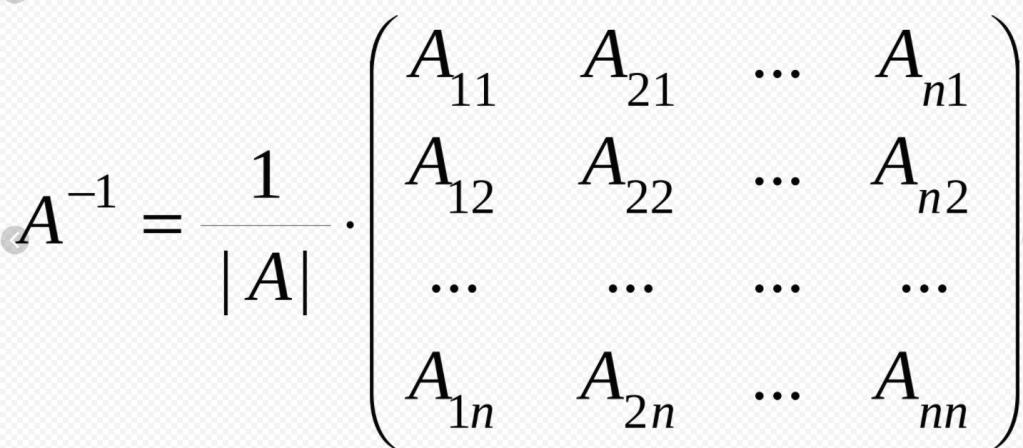
Avendo imparato che ha diversi tipi, è necessario dire sul seguente concetto: il rango di una matrice. Con questo si intende il numero di colonne lineari indipendenti o il numero di righe lineari indipendenti. Inoltre, il grado di qualsiasi matrice è l'ordine dei minori, che è il più alto, il suo determinante è diverso da zero.

Il rango è indicato dal rintocco A, ma il rango A. è stato trovato Entrambi i concetti sono considerati corretti, quindi con diverse ortografie questo non sarà considerato un errore. La cosa principale è non dimenticare che il numero di righe è sempre uguale al grado delle colonne.

Azioni sulla matrice

La matrice è un sistema universale per risolvere problemi algebrici e su di essa vengono eseguite varie azioni. Questi includono la moltiplicazione di due matrici, l'aggiunta, la moltiplicazione per il suo numero e altre matrici.

Eseguendo numerose azioni in algebra, un sistema di varie matrici aiuta a trovare un modo più semplice per risolvere i problemi. Ci vuole meno tempo e aiuta a non perdersi in molte azioni.

Le operazioni relative alla matrice sono usate non solo in matematica, ma anche in fisica e chimica.