Il fenomeno della rifrazione. Angoli di rifrazione e caduta. L'apparente profondità del serbatoio
Il fenomeno della rifrazione è un effetto visivo che si verifica quando un raggio di luce attraversa l'interfaccia tra due media che sono trasparenti ad esso. Caratteristiche importanti di questo effetto sono gli indici di rifrazione e gli angoli di incidenza e rifrazione. Consideriamo nell'articolo più in dettaglio questo fenomeno ottico.
La legge di Snell per il fenomeno della rifrazione
Come sapete, qualsiasi onda, anche elettromagnetica, si propaga in linea retta e a velocità costante in un materiale omogeneo. Non appena ci sono violazioni dell'omogeneità di questo materiale, l'onda cambia la sua traiettoria rettilinea. Un vivido esempio di tale cambiamento è la rifrazione della luce.
La rifrazione del raggio avviene in un punto localizzato nello spazio, che si trova all'interfaccia di due supporti trasparenti con caratteristiche fisiche diverse. Ad esempio, questi ambienti possono essere di vetro, aria, acqua, plastica trasparente e altri. Quando colpisce il secondo mezzo, la luce devia di un certo angolo rispetto alla traiettoria originale.
Ad
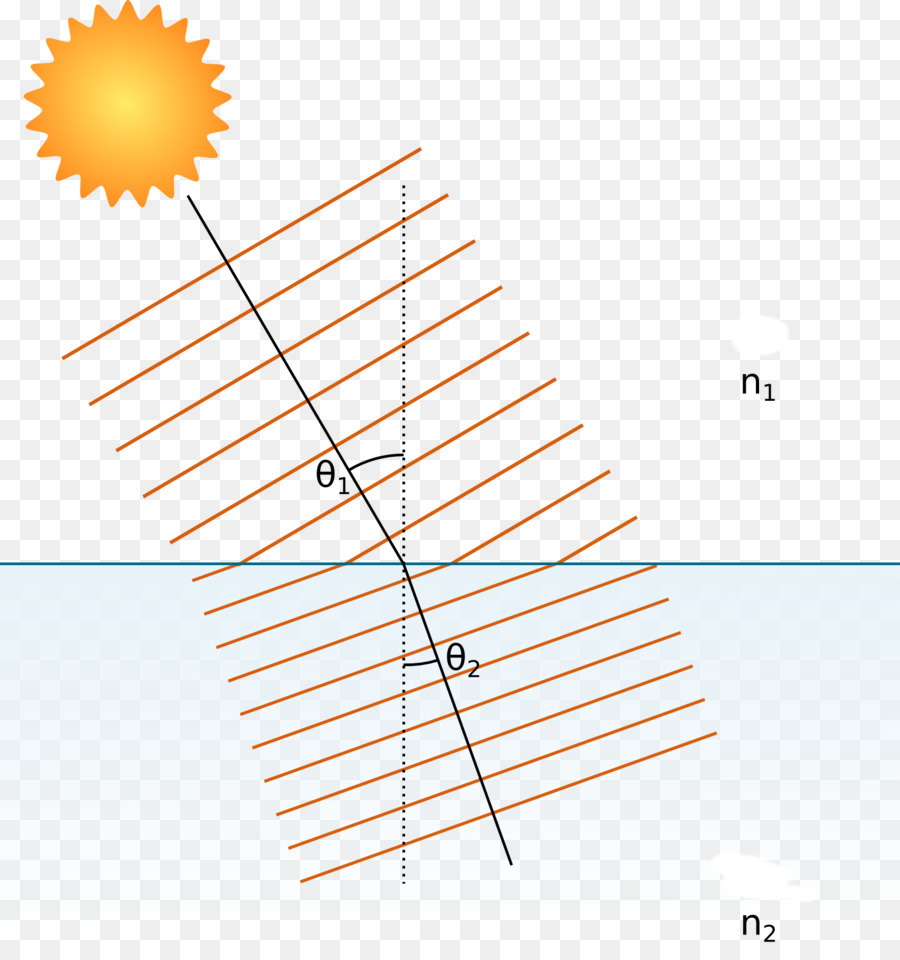
Se disegnate mentalmente una perpendicolare attraverso il punto in cui il raggio interseca il piano di separazione dei media e designate l'angolo tra la perpendicolare e il raggio come θ 1 , e l'angolo tra la stessa perpendicolare e il raggio che passava nel secondo mezzo, come θ 2 , allora la seguente relazione vale:
sin (θ 1 ) * n 1 = sin (θ 2 ) * n 2
Gli angoli di theta uno (θ 1 ) e theta due (θ 2 ) sono chiamati rispettivamente gli angoli di incidenza e rifrazione. I valori di n 1 , n 2 sono importanti caratteristiche ottiche del primo e del secondo supporto, sono chiamati indici di rifrazione.
La suddetta formula è chiamata legge Snell (Snellius), poiché lo scienziato olandese Willebrord Snellus all'inizio del XVII secolo la formò per la prima volta nella sua forma moderna, analizzando una grande quantità di materiale sperimentale.
Ad

Indice di rifrazione
Secondo la definizione matematica di questa quantità fisica, è uguale al rapporto tra le due velocità della luce: nel vuoto e nel materiale, cioè:
n = c / v
Poiché c> v, allora n sarà sempre maggiore di uno.
L'indice di rifrazione ha valori diversi per diverse sostanze. Ad esempio, per l'aria è quasi uguale a 1, e per l'acqua è 1,33. Il valore di n dipende anche dalla composizione chimica dello stesso materiale. Ad esempio, l'indice di rifrazione del vetro dipende dal tipo di quest'ultimo e va da 1,5 a 1,66.
Oltre alle proprietà del materiale, n varia notevolmente se si modifica la frequenza della luce nel raggio. L'angolo di rifrazione della luce blu è sempre maggiore del rosso. Le cifre fornite nel paragrafo precedente si riferiscono alla parte gialla dello spettro visibile da un uomo (λ ≈ 590 nm).
Densità ottica del mezzo
Questa caratteristica fisica determina quanto fortemente il mezzo rallenta la velocità della luce. La densità ottica è determinata in modo univoco dall'indice di rifrazione. Ad esempio, l'acqua è otticamente più densa dell'aria, e ogni tipo di vetro è più denso dell'acqua.
Se osservi la formula di Snell, puoi vedere che maggiore è la densità ottica del mezzo, più basso è l'angolo rispetto al normale. Questa conclusione è valida non importa da quale mezzo e in quale luce cadrà il raggio. Quindi, quando si considera il confine acqua-aria, l'angolo di rifrazione sarà inferiore all'angolo di incidenza se il raggio si sposta nell'acqua. Se cambi la direzione del raggio, allora l'angolo di incidenza sarà più piccolo.
Ad
La sfida di applicare la legge di Snell
È noto che un raggio di luce cade sulla superficie dell'acqua con un angolo di 32 ° . È necessario determinare l'angolo di rifrazione della luce, nonché l'entità della sua variazione, se si aumenta l'angolo di incidenza di 10 o .
La quantità di rifrazione della luce può essere determinata dalla legge di Snell. Abbiamo:
θ 2 = arcsin (sin (θ 1 ) * n 1 / n 2 )
Poiché la luce cade dall'aria nell'acqua, allora n 1 = 1 en 2 = 1.33. Sapendo che θ 1 = 32 o , otteniamo:
θ 2 = arcsin (sin (32 o ) * 1 / 1.33) = 23.48 o
Come puoi vedere, l'angolo è diminuito in modo significativo. Ora calcoliamo l'angolo di rifrazione del raggio, se θ 1 = 42 o . Usando la stessa formula, otteniamo:
θ 2 = arcsin (sin (42 o ) * 1 / 1.33) = 30.21 o
Prendi la differenza tra gli angoli ottenuti, otteniamo:
30.21 o - 23.48 o = 6.73 o
Il risultato ottenuto significa che i cambiamenti tra gli angoli di incidenza e rifrazione non sono lineari. Un aumento dell'angolo di incidenza di 10 o ha portato a un cambiamento nell'angolo di rifrazione solo di 6.7 o .
Il compito di determinare la profondità apparente

Molti hanno notato che se guardi il fondo del serbatoio, le pietre che si trovano su di esso e le alghe in crescita sembrano vicine alla superficie. Calcola, usando la legge della rifrazione, poiché le profondità reali e apparenti differiscono l'una dall'altra. Per questo considereremo piccoli angoli di incidenza, cioè l'osservatore guarda verticalmente verso il basso del serbatoio. Di seguito è riportata la figura corrispondente.
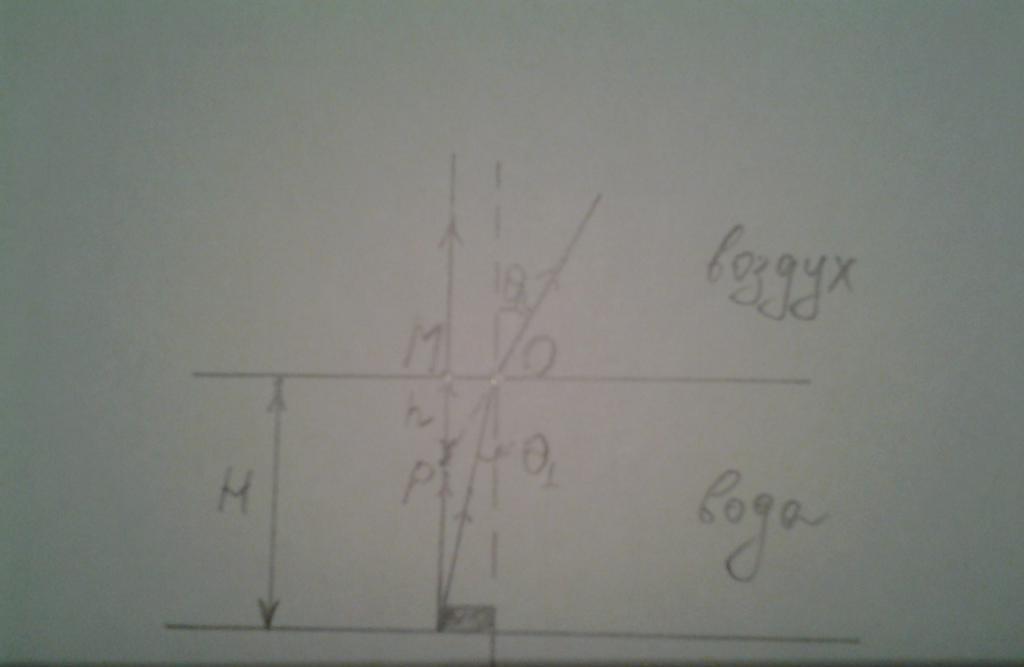
La figura mostra l'oggetto che si trova sul fondo. Poiché i due raggi che escono dallo stesso punto dell'oggetto si intersecheranno nel punto P per l'osservatore, la profondità h = MP sarà evidente.
Per trovare h, considera il triangolo destro POM. L'intervallo MO è H * tg (θ 1 ), l'angolo POM è 90 - θ2. Ora puoi scrivere:
tg (90-θ 2 ) = h / (H * tg (θ 1 ))
Sapendo che la tangente è uguale al rapporto tra seno e coseno e usando le formule per le funzioni trigonometriche, possiamo riscrivere questa uguaglianza come segue:
cos (θ 2 ) / sin (θ 2 ) = cos (θ 1 ) * h / (H * sin (θ 1 ))
Poiché consideriamo piccoli angoli (vicini alla verticale), allora i coseni saranno quasi uguali alle unità, quindi l'ultima formula sarà semplificata nella forma:
h = h * sin (θ 1 ) / sin (θ 2 )
Ma il rapporto tra i seni è uguale al rapporto inverso degli indici di rifrazione dei media secondo la legge di Snell, quindi, scriviamo:
h = H * n 2 / n 1
Mentre il raggio esce dall'acqua, n 2 è un indicatore per l'aria, che è uguale a uno. La formula finale per la profondità apparente del serbatoio quando è vista verticalmente è:
h = h / n, dove n = 1.33
Pertanto, la profondità apparente è circa il 25% in meno del reale.