La proiezione del punto sull'aereo. Proiezione di un punto su una linea retta su un piano
Studiare le proprietà delle figure nello spazio e su un piano è impossibile senza la conoscenza delle distanze tra un punto e tali oggetti geometrici come una retta e un piano. In questo articolo mostreremo come trovare queste distanze, considerando la proiezione di un punto su un piano e su una linea retta.
Equazione della linea per gli spazi bidimensionali e tridimensionali
Il calcolo delle distanze di un punto in una linea retta e un piano viene eseguito utilizzando la sua proiezione su questi oggetti. Per essere in grado di trovare queste proiezioni, si dovrebbe sapere in che forma vengono date le equazioni per le linee rette e i piani. Iniziamo con il primo.
Una retta è una raccolta di punti, ognuno dei quali può essere ottenuto dal precedente trasferendo a vettori paralleli. Per esempio, c'è un punto M e N. Il vettore MN¯ che li collega prende M a N. C'è anche un terzo punto P. Se il vettore MP¯ o NP¯ è parallelo a MN¯, allora tutti e tre i punti su una linea si trovano e formano.
A seconda della dimensione dello spazio, l'equazione che definisce la linea può cambiare forma. Pertanto, la ben nota dipendenza lineare della coordinata y su x nello spazio descrive un piano che è parallelo al terzo asse z. A questo proposito, in questo articolo considereremo solo l'equazione vettoriale per la linea. Ha lo stesso aspetto per l'aereo e lo spazio tridimensionale.
Nello spazio, una linea retta può essere definita dalla seguente espressione:
(x; y; z) = (x 0 ; y 0 ; z 0 ) + α * (a; b; c)
Qui, i valori delle coordinate con indici zero corrispondono ad una retta che appartiene ad un certo punto, u¯ (a; b; c) è le coordinate del vettore di direzione che giace su una data linea retta, α è un numero reale arbitrario, cambiando che è possibile ottenere tutti i punti della retta. Questa equazione è chiamata vettore.
Spesso l'equazione di cui sopra è scritta nella forma aperta:
x = x 0 + α * a;
y = y 0 + α * b;
z = z 0 + α * c
Allo stesso modo, possiamo scrivere l'equazione per una linea retta nel piano, cioè nello spazio bidimensionale:
(x; y) = (x 0 ; y 0 ) + α * (a; b);
x = x 0 + α * a;
y = y 0 + α * b
Equazione piana
Per essere in grado di trovare la distanza da un punto ai piani delle proiezioni, è necessario sapere come viene definito l'aereo. Così come una linea retta, può essere rappresentata in diversi modi. Qui ne consideriamo solo uno: l'equazione generale.
Supponiamo che il punto M (x 0 ; y 0 ; z 0 ) appartenga al piano e che il vettore n ¯ (A; B; C) sia perpendicolare ad esso, quindi per tutti i punti (x; y; z) del piano la seguente uguaglianza sarà vera:
A * x + B * y + C * z + D = 0, dove D = -1 * (A * x 0 + B * y 0 + C * z 0 )
Va ricordato che in questa equazione generale del piano, i coefficienti A, B e C sono le coordinate del normale al piano del vettore.
Calcolo delle distanze per coordinate
Prima di procedere alla considerazione delle proiezioni sul piano di un punto e su una linea retta, va ricordato come deve essere calcolata la distanza tra due punti noti.
Supponiamo che ci siano due punti spaziali:
A 1 (x 1 ; y 1 ; z 1 ) e A 2 (x 2 ; y 2 ; z 2 )
Quindi la distanza tra loro è calcolata dalla formula:
A 1 A 2 = √ (((x 2 -x 1 ) 2 + (y 2 -y 1 ) 2 + (z 2 -z 1 ) 2 )
Usando questa espressione, viene determinata anche la lunghezza del vettore A 1 A 2 ¯.
Per il caso su un piano, quando due punti sono dati con solo una coppia di coordinate, puoi scrivere un'equazione simile senza la presenza di un membro con z in esso:
A 1 A 2 = √ (((x 2 -x 1 ) 2 + (y 2 -y 1 ) 2 )
Ora considereremo vari casi di proiezione su un piano di un punto su una linea retta e su un piano nello spazio.
Punto, linea e distanza tra di loro
Supponiamo che ci sia un punto e una linea retta:
P 2 (x 1 ; y 1 );
(x; y) = (x 0 ; y 0 ) + α * (a; b)
La distanza tra questi oggetti geometrici corrisponderà alla lunghezza del vettore, il cui inizio si trova nel punto P 2 , e la fine è in tale punto P sulla retta indicata, per la quale il vettore P 2 P ¯ di questa retta è perpendicolare. Il punto P è chiamato la proiezione del punto P 2 sulla linea in questione.
La figura seguente mostra il punto P 2 , la sua distanza da d alla retta e anche il vettore di direzione v 1 ¯. Anche sulla linea viene scelto un punto P 1 arbitrario e da questo viene disegnato un vettore in P 2 . Il punto P qui coincide con il punto in cui la perpendicolare interseca la linea.
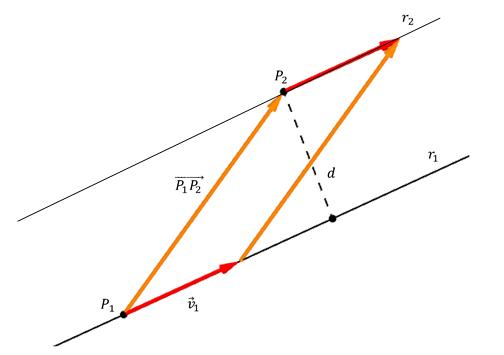
Si può vedere che le frecce arancioni e rosse formano un parallelogramma, i cui lati sono il vettore P 1 P 2 ¯ e v 1 ¯, e l'altezza è d. Dalla geometria è noto che per trovare l'altezza di un parallelogramma, la sua area deve essere divisa per la lunghezza della base, su cui è abbassata la perpendicolare. Poiché l'area del parallelogramma è calcolata come prodotto vettoriale dei suoi lati, otteniamo la formula per calcolare d:
d = | [P 1 P 2 ¯ * v 1 ¯] | / | v 1 ¯ |
Tutti i vettori e le coordinate dei punti in questa espressione sono noti, quindi puoi usarli senza eseguire alcuna trasformazione.
Sarebbe possibile risolvere questo problema in modo diverso. Per fare ciò, annota due equazioni:
- il prodotto scalare P 2 P ¯ su v 1 ¯ dovrebbe essere uguale a zero, poiché questi vettori sono reciprocamente perpendicolari;
- le coordinate del punto P devono soddisfare l'equazione di una linea.
Queste equazioni sono sufficienti per trovare le coordinate di P, e quindi la lunghezza d per la formula indicata nel paragrafo precedente.
Il compito di trovare la distanza tra la linea e il punto
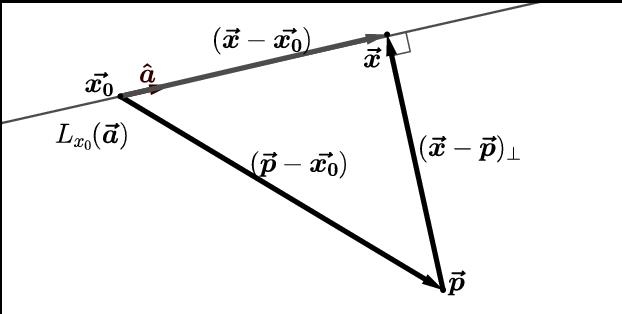
Mostriamo come usare queste informazioni teoriche per risolvere un problema specifico. Supponiamo che il punto e la linea seguenti siano noti:
M (5; -3);
(x; y) = (3; 1) - α * (0; 2)
È necessario trovare punti di proiezione su una linea retta su un piano, nonché la distanza da M a una linea retta.
Indica la proiezione che si trova dal punto M 1 (x 1 ; y 1 ). Risolviamo questo problema in due modi, descritti nel paragrafo precedente.
Metodo 1. Il vettore di direzione v 1 ¯ ha coordinate (0; 2). Per costruire un parallelogramma, scegli un punto appartenente a una linea retta. Ad esempio, un punto con coordinate (3; 1). Quindi il vettore del secondo lato del parallelogramma avrà le coordinate:
(5; -3) - (3; 1) = (2; -4)
Ora è necessario calcolare il prodotto dei vettori che definiscono i lati del parallelogramma:
[(2; -4) * (0; 2)] = 4
Sostituiamo questo valore nella formula, otteniamo la distanza da M alla linea retta:
d = 4 / √4 = 2
Metodo 2. Ora troveremo in un altro modo non solo la distanza, ma anche le coordinate della proiezione M sulla linea, come richiesto dalla condizione del problema. Come accennato in precedenza, per risolvere il problema, è necessario creare un sistema di equazioni. Sembrerà:
(x 1 -5) * 0 + (y 1 +3) * 2 = 0;
(x 1 ; y 1 ) = (3; 1) -α * (0; 2)
Risolviamo questo sistema:
y 1 = -3;
x 1 = 3
La proiezione del punto di origine della coordinata è M 1 (3; -3). Quindi la distanza richiesta è:
d = | MM 1 ¯ | = √ (4 + 0) = 2
Come potete vedere, entrambe le soluzioni hanno dato lo stesso risultato, che indica la correttezza delle operazioni matematiche eseguite.
Proiezione di un punto su un piano
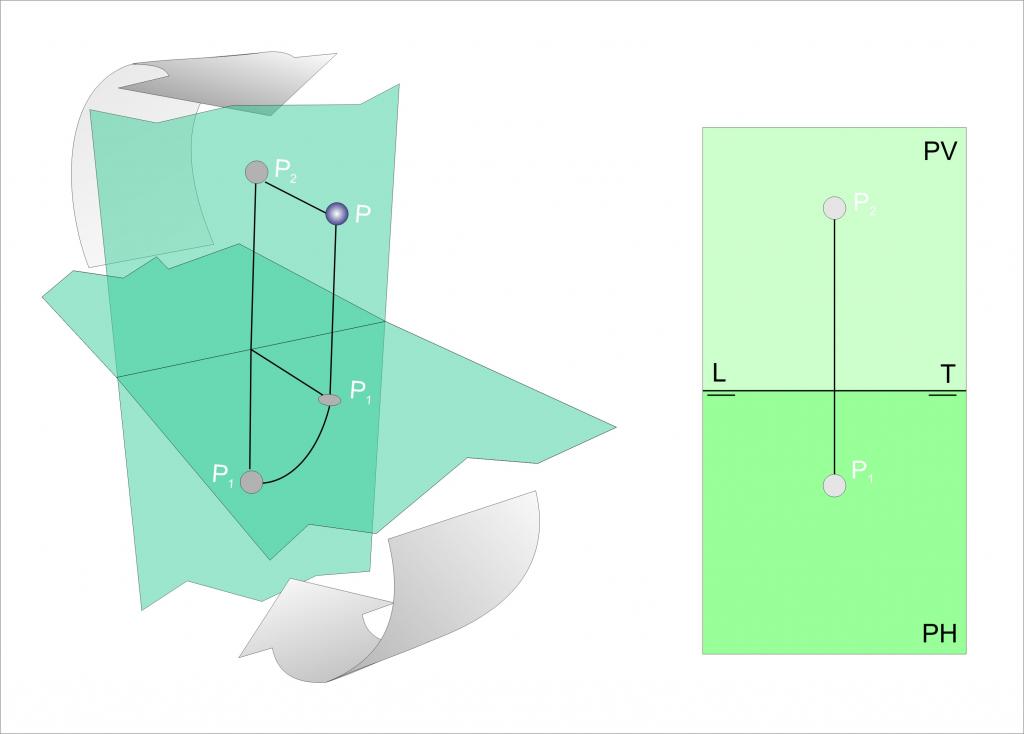
Consideriamo ora qual è la proiezione di un punto dato nello spazio su un certo piano. È facile intuire che questa proiezione è anche un punto che, insieme a quello originale, forma un vettore perpendicolare al piano.
Supponiamo che la proiezione sul piano delle coordinate del punto M sia la seguente:
M 1 (x 1 ; y 1 ; z 1 )
Il piano stesso è descritto dall'equazione:
A * x + B * y + C * z + D = 0
Sulla base di questi dati, possiamo fare l'equazione di una linea retta che attraversa il piano ad angolo retto e passa per M e M 1 :
(x; y; z) = (x 0 ; y 0 ; z 0 ) + α * (A; B; C)
Qui le variabili con indici zero sono le coordinate del punto M. È possibile calcolare la posizione sul piano del punto M 1 partendo dal presupposto che le sue coordinate devono soddisfare entrambe le equazioni scritte. Se queste equazioni non sono sufficienti per risolvere il problema, è possibile utilizzare la condizione del parallelismo MM 1 ¯ e il vettore di direzione per il piano dato.
Ovviamente, la proiezione di un punto appartenente ad un piano coincide con se stessa e la distanza corrispondente è zero.
Compito con punto e piano
Sia dato il punto M (1; -1; 3) e il piano, che è descritto dalla seguente equazione generale:
-x + 3 * y -2 * z + 4 = 0
È necessario calcolare le coordinate della proiezione sul piano del punto e calcolare la distanza tra questi oggetti geometrici.
Per cominciare, costruiamo l'equazione di una linea che passa per M e perpendicolare al piano indicato. Sembra:
(x; y; z) = (1; -1; 3) + α * (- 1; 3; -2)
Indica il punto in cui questa linea retta interseca il piano, M 1 . Le eguaglianze per un piano e una linea retta devono essere soddisfatte se sostituiamo le coordinate M 1 in esse. Scrivendo in forma esplicita l'equazione di una linea retta, otteniamo le seguenti quattro equazioni:
-x 1 + 3 * y 1 -2 * z 1 + 4 = 0;
x 1 = 1 - α;
y 1 = -1 + 3 * α;
z 1 = 3 - 2 * α
Dall'ultima uguaglianza otteniamo il parametro α, quindi lo sostituiamo nella penultima e nella seconda espressione, otteniamo:
α = (3-z 1 ) / 2;
y 1 = -1 + 3 * (3-z 1 ) / 2 = -3 / 2 * z 1 + 3,5;
x 1 = 1 - (3-z 1 ) / 2 = 1/2 * z 1 - 1/2
L'espressione per y 1 e x 1 è sostituita nell'equazione per il piano, abbiamo:
-1 * (1/2 * z 1 - 1/2) + 3 * (- 3/2 * z 1 + 3,5) -2 * z 1 + 4 = 0
Dove prendiamo:
z 1 = 15/7
poi:
y 1 = -3 / 2 * 15/7 + 3,5 = 2/7;
x 1 = 1/2 * 15/7 - 1/2 = 4/7
Abbiamo determinato che la proiezione del punto M su un dato piano corrisponde alle coordinate (4/7; 2/7; 15/7).
Ora calcola la distanza | MM 1 ¯ |. Le coordinate del vettore corrispondente sono:
MM 1 ¯ (-3/7; 9/7; -6/7)
La distanza richiesta è:
d = | MM 1 ¯ | = √126 / 7 ≈ 1.6
Tre punti di proiezione
Durante la produzione di disegni, è spesso necessario ottenere proiezioni di sezioni su tre piani reciprocamente perpendicolari. Pertanto, è utile considerare quali saranno le proiezioni di un certo punto M con coordinate (x 0 ; y 0 ; z 0 ) su tre piani coordinati.

Non è difficile mostrare che il piano xy è descritto dall'equazione z = 0, il piano xz corrisponde all'espressione y = 0, e il piano yz rimanente è denotato dall'uguaglianza x = 0. È facile intuire che le proiezioni di un punto su 3 piani saranno uguali:
per x = 0: (0; y 0 ; z 0 );
per y = 0: (x 0 ; 0; z 0 );
per z = 0: (x 0 ; y 0 ; 0)
Dove è importante conoscere le proiezioni del punto e la sua distanza dagli aerei?
Determinare la posizione della proiezione di punti su un dato piano è importante quando si trovano quantità come superficie e volume per prismi obliqui e piramidi. Ad esempio, la distanza dalla cima della piramide al piano della base è l'altezza. Quest'ultimo è incluso nella formula per il volume di questa figura.
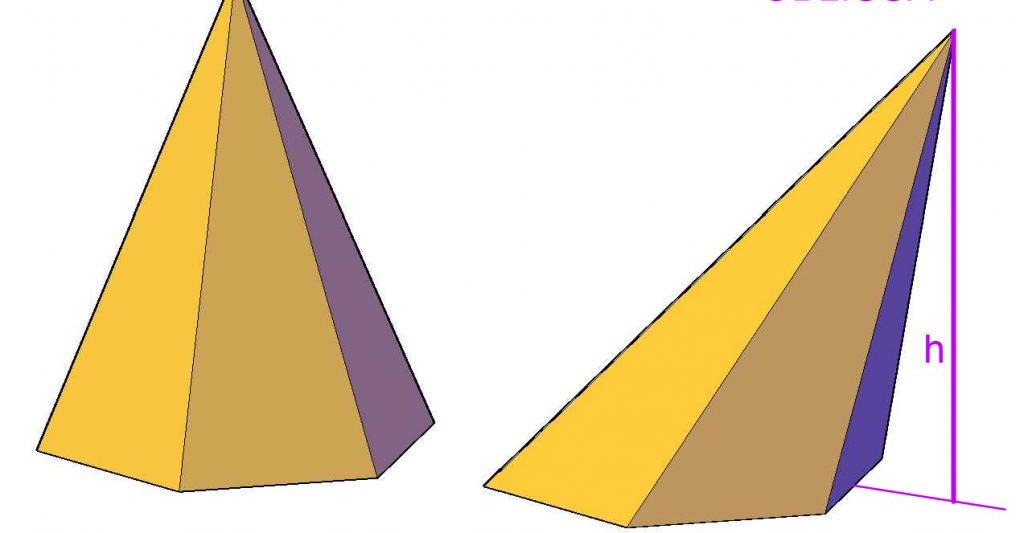
Le formule e i metodi considerati per determinare le proiezioni e le distanze da un punto a una retta e il piano sono abbastanza semplici. È importante solo memorizzare le forme corrispondenti del piano e le equazioni dirette e anche avere una buona immaginazione spaziale per applicarle con successo.