Le regole con cui l'aggiunta di vettori

Come è l'aggiunta di vettori, non è sempre chiaro agli studenti. I bambini non rappresentano ciò che sta dietro di loro. Devi solo memorizzare le regole e non meditare sull'essenza. Pertanto, si tratta dei principi di addizione e sottrazione di quantità di vettori che richiedono molta conoscenza.

Come risultato dell'aggiunta di due o più vettori, si ottiene sempre uno. Inoltre, sarà sempre lo stesso indipendentemente dalla ricezione della sua posizione.

Molto spesso nel corso di geometria della scuola viene considerata l'aggiunta di due vettori. Può essere eseguito dalla regola di un triangolo o parallelogramma. Queste immagini hanno un aspetto diverso, ma il risultato dell'azione è uno.

Com'è l'aggiunta della regola del triangolo?

Viene utilizzato quando i vettori non sono collineari. Cioè, non mentire su una linea o su linee parallele.

In questo caso, il primo vettore dovrebbe essere posticipato da qualche punto arbitrario. Dalla sua estremità è richiesto di condurre un parallelo e uguale al secondo. Il risultato sarà un vettore che parte dall'inizio del primo e finisce alla fine del secondo. La figura assomiglia a un triangolo. Da qui il nome della regola.

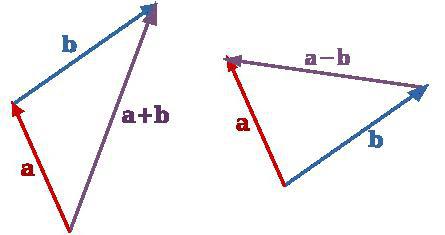
Se i vettori sono collineari, allora questa regola può anche essere applicata. Solo il disegno si troverà lungo una linea.

Com'è l'aggiunta secondo la regola del parallelogramma?

Anche in questo caso? si applica solo ai vettori non collineari. La costruzione viene eseguita su un principio diverso. Anche se l'inizio è lo stesso. È necessario posticipare il primo vettore. E dal suo inizio - il secondo. Sulla base di essi, completa il parallelogramma e disegna una diagonale dall'inizio di entrambi i vettori. Lei sarà il risultato. Questo è il modo di aggiungere i vettori secondo la regola del parallelogramma.

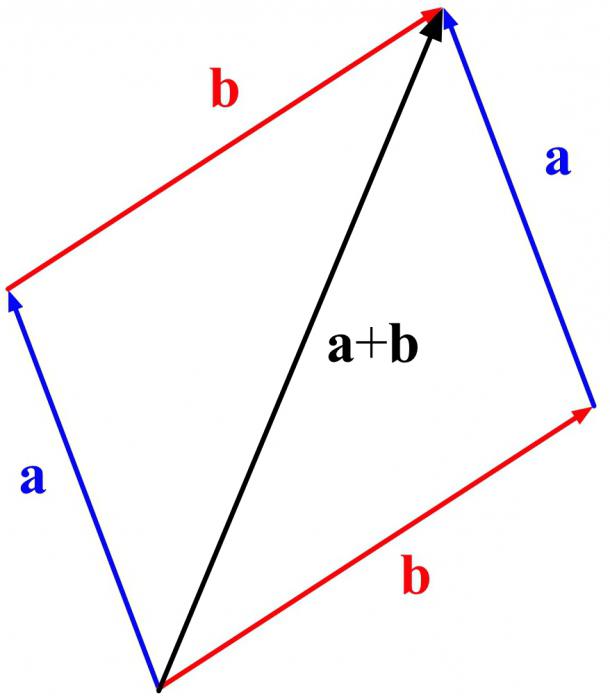
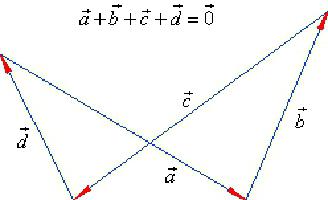
Finora, ce ne sono stati due. E se ci fossero 3 o 10? Usa il seguente trucco.

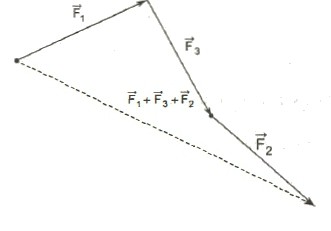
Come e quando si applica la regola del poligono?

Se si desidera eseguire l'aggiunta di vettori, il cui numero è maggiore di due, non si dovrebbe avere paura. È sufficiente rimandarli tutti in sequenza e collegare l'inizio della catena alla sua fine. Questo vettore sarà la somma desiderata.

Quali proprietà sono valide per le azioni con i vettori?

Circa il vettore zero. Che asserisce che quando aggiunto con esso, l'originale è ottenuto.

Sul vettore opposto. Cioè, uno che ha la direzione opposta ed è uguale in grandezza al valore. La loro somma sarà uguale a zero.

Sulla commutatività dell'aggiunta. Ciò che è noto fin dalla scuola elementare. Cambiare i posti degli oggetti non cambia il risultato. In altre parole, non importa quale vettore rimandare per primo. La risposta sarà ancora corretta e unica.

Sull'associatività dell'aggiunta. Questa legge consente di aggiungere a coppie tutti i vettori di una tripla e aggiungerne una terza. Se lo scrivi con l'aiuto dei segni, ottieni quanto segue:

prima + (seconda + terza) = seconda + (prima + terza) = terza + (prima + seconda).

Cosa si sa della differenza dei vettori?

Un'operazione di sottrazione separata non esiste. Ciò è dovuto al fatto che è, in effetti, un'aggiunta. Solo il secondo di loro è indicato nella direzione opposta. E poi tutto è fatto come se si considerasse l'aggiunta vettoriale. Pertanto, praticamente non parlano delle loro differenze.

Per semplificare il lavoro con la loro sottrazione, la regola del triangolo è stata modificata. Ora (sottraendo) il secondo vettore deve essere posticipato dall'inizio del primo. La risposta sarà quella che connette il punto finale della franchigia con esso. Sebbene tu possa rimandare come descritto in precedenza, semplicemente cambiando la direzione del secondo.

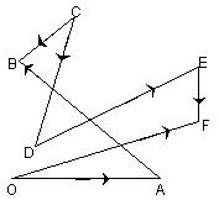
Come trovare la somma e la differenza di vettori in coordinate?

Il problema fornisce le coordinate dei vettori e devi conoscere i loro valori per la finale. In questa costruzione non è necessario eseguire. Cioè, puoi usare semplici formule che descrivono la regola di aggiunta di vettori. Sembrano così:

a (x, y, z) + in (k, l, m) = c (x + k, y + l, z + m);

a (x, y, z) -c (k, l, m) = c (xk, yl, zm).

È facile notare che le coordinate che devi solo aggiungere o sottrarre dipendono dal compito specifico.

Il primo esempio con la soluzione

Condizioni. Dato un rettangolo AVSD. I suoi lati sono 6 e 8 cm Il punto di intersezione delle diagonali è indicato dalla lettera O. È necessario calcolare la differenza tra i vettori AO e VO.

La decisione Per prima cosa devi disegnare questi vettori. Sono diretti dai vertici del rettangolo al punto di intersezione delle diagonali.

Se osservate attentamente il disegno, potete vedere che i vettori sono già allineati in modo che il secondo di essi sia in contatto con la fine del primo. È solo che la sua direzione è sbagliata. Deve iniziare da questo punto. Questo è se i vettori sono sommati e nel problema - sottrazione. Stop. Questa azione significa che devi aggiungere un vettore diretto opposto. Ciò significa che VO deve essere sostituito con OB. E si scopre che due vettori hanno già formato una coppia di lati dalla regola di un triangolo. Pertanto, il risultato della loro aggiunta, cioè la differenza desiderata, è il vettore AB.

E coincide con il lato del rettangolo. Per registrare una risposta numerica, sarà richiesto quanto segue. Disegna un rettangolo lungo in modo che il lato grande vada in orizzontale. La numerazione dei vertici inizia dal basso a sinistra e va in senso antiorario. Quindi la lunghezza del vettore AB sarà pari a 8 cm.

La risposta è La differenza tra AO e VO è di 8 cm.

Il secondo esempio e la sua soluzione dettagliata

Condizioni. Il rombo AVSD diagonale è uguale a 12 e 16 cm Il punto della loro intersezione è indicato dalla lettera O. Calcola la lunghezza del vettore formato dalla differenza tra i vettori AO e VO.

La decisione Lascia che la designazione dei vertici di un rombo sia la stessa del problema precedente. Analogamente alla soluzione del primo esempio, risulta che la differenza desiderata è uguale al vettore AB. E la sua lunghezza è sconosciuta. La soluzione del problema è stata ridotta per calcolare uno dei lati del rombo.

A tal fine, è necessario considerare il triangolo ABO. È rettangolare, poiché la diagonale del rombo si interseca con un angolo di 90 gradi. E le sue gambe sono uguali a metà delle diagonali. Cioè, 6 e 8 cm Il lato cercato nel problema coincide con l'ipotenusa in questo triangolo.

Per trovarlo, abbiamo bisogno del teorema di Pitagora. Il quadrato dell'ipotenusa sarà uguale alla somma dei numeri 6 ² e 8 ² . Dopo la quadratura, i valori sono 36 e 64. La loro somma è 100. Da ciò ne consegue che l'ipotenusa è 10 cm.

La risposta è La differenza tra i vettori di AO e HE è 10 cm.

Il terzo esempio con una soluzione dettagliata

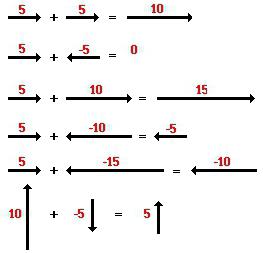
Condizioni. Calcola la differenza e la somma di due vettori. Le loro coordinate sono note: nel primo - 1 e 2, nel secondo - 4 e 8.

La decisione Per trovare l'importo dovrai aggiungere a coppie le prime e le seconde coordinate. Il risultato saranno i numeri 5 e 10. La risposta sarà un vettore con coordinate (5; 10).

Per la differenza è necessario eseguire la sottrazione delle coordinate. Dopo aver eseguito questa azione, ottieni i numeri -3 e -6. Saranno le coordinate del vettore desiderato.

La risposta è La somma dei vettori è (5; 10), la loro differenza è (-3; -6).

Quarto esempio

Condizioni. La lunghezza del vettore AB è 6 cm, BC - 8 cm, il secondo è tracciato dalla fine del primo con un angolo di 90 gradi. Calcola: a) la differenza dei moduli dei vettori BA e BC e il modulo della differenza BA e BC; b) la somma degli stessi moduli e il modulo della somma.

Soluzione: a) Le lunghezze dei vettori sono già state fornite nel problema. Pertanto, calcolare la loro differenza non è difficile. 6 - 8 = -2. La situazione con il modulo differenza è un po 'più complicata. Per prima cosa devi sapere quale vettore sarà il risultato della sottrazione. A questo scopo, si dovrebbe posticipare il vettore BA, che è diretto nella direzione opposta AB. Quindi dalla sua estremità per tenere il vettore del sole, dirigendolo nella direzione opposta all'originale. Il risultato della sottrazione è il vettore CA. Il suo modulo può essere calcolato dal teorema di Pitagora. I calcoli semplici portano a un valore di 10 cm.

b) La somma dei moduli dei vettori è di 14 cm. Per cercare la seconda risposta, è necessaria una conversione. Il vettore BA è diretto opposto a quello dato da - AB. Entrambi i vettori sono diretti da un punto. In questa situazione, puoi usare la regola del parallelogramma. Il risultato dell'aggiunta sarà una diagonale e non solo un parallelogramma, ma un rettangolo. Le sue diagonali sono uguali, il che significa che il modulo della somma è lo stesso del paragrafo precedente.

Risposta: a) -2 e 10 cm; b) 14 e 10 cm.