Spazio tridimensionale: vettori, coordinate

Anche dal corso di algebra e geometria della scuola conosciamo il concetto di spazio tridimensionale. Se per capire, il termine "spazio tridimensionale" è definito come un sistema di coordinate con tre dimensioni (tutti lo sanno). In effetti, è possibile descrivere qualsiasi oggetto volume con l'aiuto di lunghezza, larghezza e altezza nel senso classico. Tuttavia, diciamo, scaviamo un po 'più a fondo.

Cos'è lo spazio tridimensionale

Come è già diventato chiaro, la comprensione dello spazio tridimensionale e degli oggetti capaci di esistere al suo interno è determinata da tre concetti principali. È vero, nel caso di un punto questi sono esattamente tre valori, e nel caso di linee rette, curve, linee spezzate o oggetti volume, le coordinate corrispondenti possono essere più grandi.

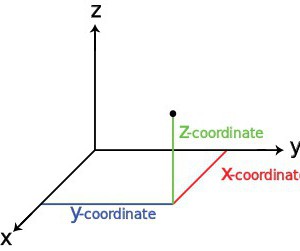
In questo caso, tutto dipende dal tipo di oggetto e dal sistema di coordinate applicato. Oggi il sistema cartesiano, a volte chiamato anche rettangolare, è considerato il più comune (classico). Lei e alcune altre specie saranno discusse più tardi.

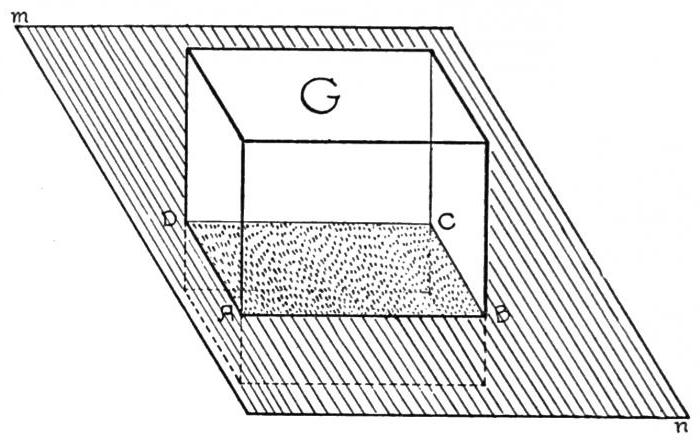
Tra le altre cose, qui è necessario distinguere tra concetti astratti (se è possibile dirlo, informi) come punti, linee rette o piani che hanno dimensioni finite o anche volume. Per ognuna di queste definizioni, ci sono anche le proprie equazioni che descrivono la loro possibile posizione nello spazio tridimensionale. Ma ora non lo è.

Il concetto di un punto nello spazio tridimensionale

Per cominciare, definiamo cos'è un punto nello spazio tridimensionale. In generale, si può chiamare una certa unità di base che definisce qualsiasi figura piana o tridimensionale, una linea, un segmento, un vettore, un piano, ecc.

Il punto stesso è caratterizzato da tre coordinate principali. Per loro, in un sistema rettangolare, vengono utilizzate guide speciali, chiamate assi X, Y e Z, i primi due assi utilizzati per esprimere la posizione orizzontale dell'oggetto e il terzo si riferisce alla specifica verticale delle coordinate. Naturalmente, per la comodità di esprimere la posizione di un oggetto rispetto alle coordinate zero nel sistema, si assumono valori positivi e negativi. Tuttavia, oggi puoi trovare altri sistemi.

Varietà di sistemi di coordinate

Come già accennato, il sistema di coordinate rettangolari creato da Descartes è oggi il principale. Tuttavia, in alcune tecniche per definire la posizione di un oggetto nello spazio tridimensionale, vengono utilizzate alcune altre varietà.

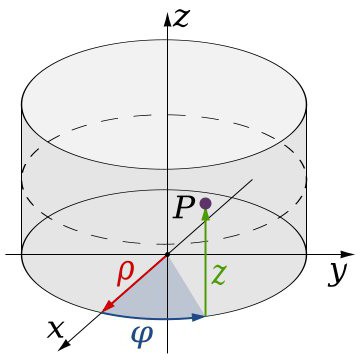
I più famosi sono i sistemi cilindrici e sferici. La differenza rispetto a quella classica è che quando si specificano gli stessi tre valori che determinano la posizione di un punto nello spazio tridimensionale, uno dei valori è angolare. In altre parole, in tali sistemi viene utilizzato un cerchio corrispondente ad un angolo di 360 gradi. Da qui e il compito specifico delle coordinate, inclusi elementi quali raggio, angolo e generatrice. Le coordinate nello spazio tridimensionale (sistema) di questo tipo obbediscono a leggi un po 'diverse. Il loro compito in questo caso è controllato dalla regola della mano destra: se si combinano il pollice e l'indice con gli assi X e Y, rispettivamente, le dita rimanenti in una posizione piegata indicheranno la direzione dell'asse Z.

Il concetto di una linea nello spazio tridimensionale

Ora alcune parole su ciò che costituisce una linea retta nello spazio tridimensionale. Basato sul concetto di base di una linea retta, questo è un tipo di linea infinita tracciata attraverso un punto o due, senza contare l'insieme di punti situati in una sequenza che non cambia il passaggio diretto della linea attraverso di essi.

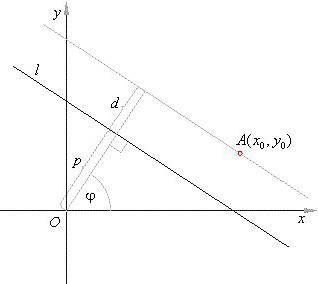
Se guardi una linea tracciata attraverso due punti nello spazio tridimensionale, dovrai prendere in considerazione le tre coordinate di entrambi i punti. Lo stesso vale per segmenti e vettori. Questi ultimi determinano la base dello spazio tridimensionale e della sua dimensione.

Definizione dei vettori e la base dello spazio tridimensionale

Come si crede comunemente, nel sistema di coordinate tridimensionale possono esserci tre vettori principali che definiscono una base. Inoltre, le basi con i corrispondenti tre vettori indipendenti possono essere innumerevoli.

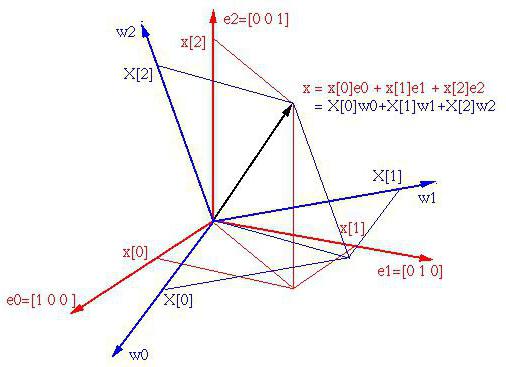
Si noti che possono esistere solo tre vettori, ma qui è possibile definire un massimo di tripli di vettori. La dimensione dello spazio è determinata dal numero di vettori linearmente indipendenti (nel nostro caso, tre). E lo spazio in cui vi è un numero finito di tali vettori è chiamato finito-dimensionale.

Vettori dipendenti e indipendenti

Per quanto riguarda la definizione di vettori dipendenti e indipendenti, i vettori che sono proiezioni (ad esempio, i vettori dell'asse X proiettati sull'asse Y) sono considerati linearmente indipendenti.

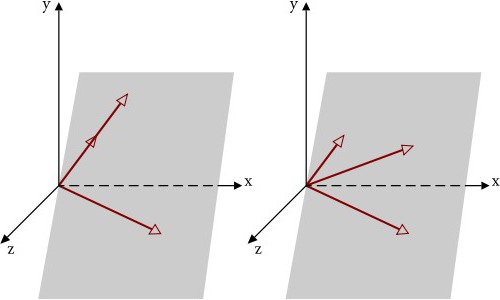
Come è già chiaro, ogni quarto vettore dipende (la teoria degli spazi lineari). Ma tre vettori indipendenti nello spazio tridimensionale non dovrebbero necessariamente trovarsi sullo stesso piano. Inoltre, se definiamo i vettori indipendenti nello spazio tridimensionale, essi non possono essere, per così dire, una continuazione dell'altro. Come è già chiaro, nel caso in cui stiamo considerando con tre dimensioni, secondo la teoria generale, possono essere costruiti solo tre tripli di vettori linearmente indipendenti in un certo sistema di coordinate (indipendentemente dal tipo).

Piano nello spazio tridimensionale

Se consideriamo il concetto di un piano, senza entrare nelle definizioni matematiche, per una comprensione più semplice di questo termine, un tale oggetto può essere considerato solo bidimensionale. In altre parole, è una collezione infinita di punti in cui una delle coordinate è una costante (costante).

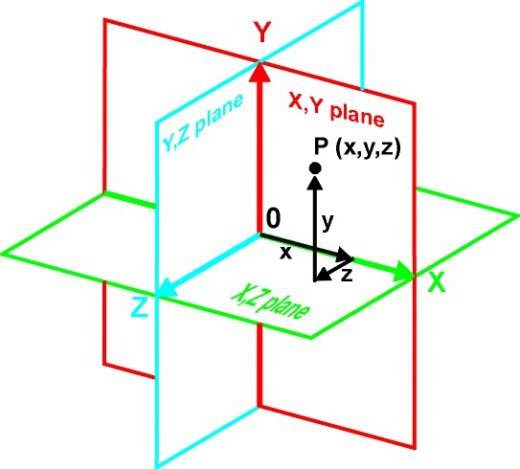
Ad esempio, un piano può essere chiamato qualsiasi numero di punti con coordinate diverse lungo gli assi X e Y, ma con le stesse coordinate lungo l'asse Z. In ogni caso, una delle coordinate tridimensionali rimane invariata. Tuttavia, questo è, per così dire, un caso generale. In alcune situazioni, lo spazio tridimensionale può intersecarsi con un piano lungo tutti gli assi.

C'è più di tre dimensioni

La domanda su quante misure possono esistere è abbastanza interessante. Si ritiene che non viviamo in tridimensionalità dal punto di vista classico dello spazio, ma in quattro dimensioni. Oltre alle lunghezze, alle larghezze e alle altezze note, questo spazio include anche la durata dell'oggetto, e il tempo e lo spazio sono strettamente interconnessi. Ciò è stato dimostrato da Einstein nella sua teoria della relatività, sebbene ciò si riferisca più alla fisica che all'algebra e alla geometria.

Un altro fatto interessante è che oggi gli scienziati hanno già dimostrato l'esistenza di almeno dodici dimensioni. Naturalmente, lontano da tutti, sarà in grado di capire quello che sono, poiché si riferisce piuttosto a una certa area astratta che è al di fuori della percezione umana del mondo. Tuttavia, il fatto rimane. E non è per niente che molti antropologi e storici sostengono che i nostri antenati potrebbero avere alcuni specifici organi di senso sviluppati come il terzo occhio, che hanno aiutato a percepire la realtà multidimensionale, e non solo lo spazio tridimensionale.

A proposito, oggi ci sono parecchie opinioni sul fatto che la percezione extrasensoriale è anche una delle manifestazioni della percezione del mondo multidimensionale, e si possono trovare molte prove.

Nota che le equazioni e i teoremi di base moderni descrivono spazi multidimensionali diversi dal nostro mondo a quattro dimensioni, ma non è sempre possibile. E la scienza in quest'area si riferisce più al campo delle teorie e delle ipotesi che a ciò che può essere sentito chiaramente o, per così dire, toccato o visto di prima mano. Tuttavia, prove indirette per l'esistenza di mondi multidimensionali, in cui possono esserci quattro o più dimensioni, non sono oggi in dubbio.

conclusione

In generale, abbiamo brevemente esaminato i concetti di base relativi allo spazio tridimensionale e alle definizioni di base. Naturalmente, ci sono molti casi speciali associati a diversi sistemi di coordinate. Inoltre, abbiamo cercato di non entrare nel caos della matematica per spiegare i termini di base, solo così che la domanda ad essi connessa è comprensibile a qualsiasi scolaro (per così dire, la spiegazione è "sulle dita").

Tuttavia, sembra che anche da interpretazioni così semplici si possa concludere che l'aspetto matematico di tutte le componenti incluse nel corso elementare di algebra e geometria.