Vettore. Cos'è un vettore?

Tale concetto come vettore è considerato in quasi tutte le scienze naturali e può avere significati completamente diversi, quindi è impossibile dare una definizione univoca di un vettore per tutte le aree. Ma proviamo a capirlo. Allora, cos'è un vettore?

Il concetto di vettore nella geometria classica

Un vettore in geometria è un segmento per il quale è indicato quale dei suoi punti è l'inizio e quale è la fine. Cioè, per dirla più semplicemente, un vettore è un segmento diretto.

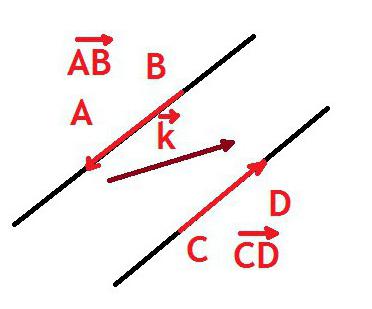
Di conseguenza, il vettore è denotato (ciò che è considerato sopra), così come il segmento, cioè due in lettere maiuscole Alfabeto latino con un trattino o una freccia che punta a destra dall'alto. Puoi anche firmarlo con una lettera minuscola (piccola) dell'alfabeto latino con un trattino o una freccia. La freccia è sempre diretta a destra e non cambia a seconda della posizione del vettore.

Quindi, il vettore ha direzione e lunghezza.

La designazione del vettore contiene la sua direzione. Questo è espresso come nella figura sottostante.

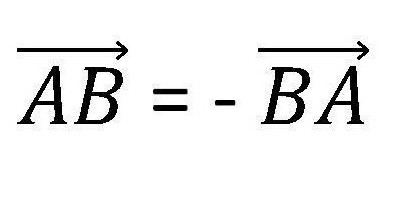
Cambiare direzione cambia il valore del vettore al contrario.

La lunghezza di un vettore è la lunghezza del segmento da cui è formato. È denotato come un modulo di un vettore. Questo è mostrato nella figura sottostante.

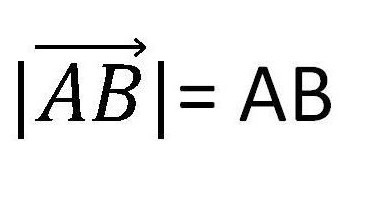
Di conseguenza, zero è un vettore la cui lunghezza è zero. Ne consegue che il vettore zero è un punto, e i punti di inizio e fine coincidono in esso.

La lunghezza del vettore - il valore non è sempre negativo. In altre parole, se c'è un segmento, allora ha necessariamente una certa lunghezza o è un punto, quindi la sua lunghezza è uguale a zero.

Il concetto di un punto è fondamentale e non ha definizione.

Aggiunta vettoriale

Esistono formule e regole speciali per i vettori con cui è possibile aggiungere.

Regola del triangolo per aggiunte vettoriali in base a questa regola, è sufficiente combinare la fine del primo vettore e l'inizio del secondo, mentre si utilizza la traduzione parallela e collegarli. Il terzo vettore risultante sarà uguale all'aggiunta degli altri due.

Regola parallellogramma. Per l'aggiunta secondo questa regola, è necessario disegnare entrambi i vettori da un punto e quindi disegnare un altro vettore dalla fine di ciascuno. Cioè, il secondo sarà disegnato dal primo vettore e il primo dal secondo. Il risultato è un nuovo punto di intersezione e si forma un parallelogramma. Se combiniamo il punto di intersezione degli inizi e delle estremità dei vettori, il vettore risultante sarà il risultato dell'aggiunta.

Allo stesso modo, è possibile eseguire e sottrarre.

Differenza di vettore

Simile all'aggiunta vettoriale, è possibile sottrarli. Si basa sul principio mostrato nella figura sottostante.

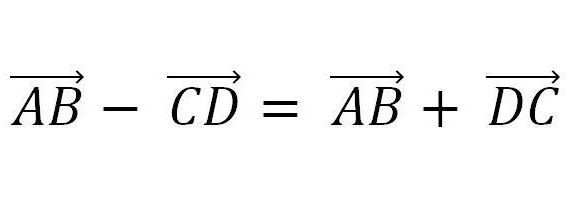
Cioè, è sufficiente rappresentare il vettore sottratto nella forma di un vettore, il contrario di esso, e calcolare secondo i principi di addizione.

Inoltre, assolutamente qualsiasi vettore diverso da zero può essere moltiplicato per qualsiasi numero k, questo cambierà la sua lunghezza k volte.

Oltre a questi, ci sono altre formule di vettori (per esempio, per esprimere la lunghezza di un vettore attraverso le sue coordinate).

Posizione dei vettori

Sicuramente, molti si sono trovati di fronte a un concetto come un vettore collineare. Cos'è la collinearità?

La collinearità dei vettori è l'equivalente delle linee parallele. Se due vettori si trovano su linee rette che sono parallele tra loro, o su una linea retta, allora tali vettori sono chiamati collineari.

Direzione. Rispetto l'uno all'altro, i vettori collineari possono essere co-diretti o opposti, questo è determinato dalla direzione dei vettori. Di conseguenza, se il vettore è co-diretto con un altro, allora il vettore opposto ad esso è diretto opposto.

La prima figura mostra due vettori diretti opposti e il terzo, che non è collineare a loro.

Dopo l'introduzione delle proprietà di cui sopra, è possibile dare una definizione e vettori uguali - questi sono vettori che sono diretti nella stessa direzione e hanno la stessa lunghezza di segmenti da cui sono formati.

In molte scienze, viene anche usato il concetto di un vettore raggio. Tale vettore descrive la posizione di un punto del piano rispetto ad un altro punto fisso (spesso questa è l'origine).

Vettori in fisica

Supponiamo che quando si risolve un problema sia sorta una condizione: il corpo si muove alla velocità di 3 m / s. Ciò significa che il corpo si muove con una direzione specifica in una linea retta, quindi questa variabile sarà un valore vettoriale. Per la soluzione, è importante conoscere sia il valore che la direzione, poiché, a seconda della considerazione, la velocità può essere pari a 3 m / se -3 m / s.

In generale, il vettore in fisica viene utilizzato per indicare la direzione della forza che agisce sul corpo e per determinare il risultante.

Quando queste forze sono indicate nella figura, sono indicate da frecce con la firma del vettore sopra di esso. Classicamente, la lunghezza della freccia è altrettanto importante, con l'aiuto di essa indicano quale forza agisce più forte, ma questa proprietà laterale non vale la pena affidarsi ad essa.

Vettore in algebra lineare e analisi matematica

Gli elementi di spazi lineari sono anche chiamati vettori, ma in questo caso sono un sistema ordinato di numeri che descrivono alcuni degli elementi. Pertanto, la direzione in questo caso non ha più importanza. Definizione vettoriale in geometria classica e in analisi matematica varia notevolmente.

Vettori di proiezione

Vettore proiettato - che cos'è?

Molto spesso, per un calcolo corretto e conveniente, è necessario espandere il vettore nello spazio bidimensionale o tridimensionale, lungo gli assi delle coordinate. Questa operazione è necessaria, ad esempio, in meccanica quando si calcolano le forze che agiscono sul corpo. Il vettore in fisica è usato abbastanza spesso.

Per eseguire una proiezione, è sufficiente abbassare le perpendicolari dall'inizio e dalla fine del vettore su ciascuno degli assi delle coordinate, i segmenti ottenuti su di essi saranno chiamati la proiezione del vettore sull'asse.

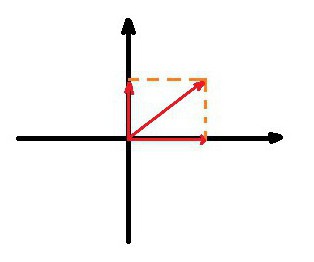
Per calcolare la lunghezza della proiezione, è sufficiente moltiplicare la sua lunghezza iniziale di una certa funzione trigonometrica, che si ottiene risolvendo un mini-problema. In sostanza, c'è triangolo rettangolo in cui l'ipotenusa è il vettore originale, una delle gambe è una proiezione e l'altra è una perpendicolare abbassata.