Quali sono i metodi di ottimizzazione? Metodi di ottimizzazione delle decisioni di gestione

La soluzione più accettabile che viene presa a livello manageriale per quanto riguarda qualsiasi problema è considerata ottimale, e il processo della sua ricerca è considerato un'ottimizzazione.

L'interdipendenza e la complessità degli aspetti organizzativi, socioeconomici, tecnici e di altro tipo della gestione della produzione sono ora ridotte a prendere decisioni gestionali che riguardano un gran numero di fattori diversi strettamente intrecciati tra loro, il che rende impossibile analizzarli separatamente usando il tradizionale metodi.

La maggior parte dei fattori è decisiva nel processo decisionale, e sono (in sostanza) non suscettibili a qualsiasi caratterizzazione quantitativa. Ci sono anche quelli che sono praticamente invariati. A questo proposito, è diventato necessario sviluppare metodi speciali che possano garantire la selezione di importanti decisioni gestionali nell'ambito di complessi compiti organizzativi, economici, tecnici (valutazioni di esperti, ricerca operativa e metodi di ottimizzazione, ecc.).

I metodi mirati allo studio delle operazioni sono utilizzati al fine di trovare soluzioni ottimali in aree di gestione quali l'organizzazione dei processi di produzione e trasporto, la pianificazione su larga scala produzione, materiale e fornitura tecnica.

I metodi per ottimizzare le soluzioni sono di studiare confrontando le stime numeriche di un numero di fattori, la cui analisi con metodi tradizionali non può essere eseguita. La soluzione ottimale è la migliore tra le possibili opzioni per quanto riguarda sistema economico e il più accettabile in relazione ai singoli elementi del sistema è subottimale.

L'essenza delle operazioni sui metodi di ricerca

Come accennato in precedenza, costituiscono i metodi per ottimizzare le decisioni di gestione. La loro base sono modelli matematici (deterministici), probabilistici che rappresentano il processo, l'attività o il sistema oggetto di studio. Questo tipo di modello rappresenta una caratteristica quantitativa del problema corrispondente. Servono come base per prendere importanti decisione di gestione nel processo di ricerca opzione accettabile in modo ottimale.

L'elenco delle questioni che svolgono un ruolo significativo per i direttori diretti della produzione e che vengono risolti nel corso dell'utilizzo dei metodi considerati:

• il grado di validità delle soluzioni scelte;
• quanto sono migliori di quelli alternativi;
• grado di considerazione dei fattori determinanti;
• qual è il criterio di ottimalità delle soluzioni selezionate.

Questi metodi per l'ottimizzazione delle soluzioni (manageriali) mirano a trovare soluzioni ottimali per il maggior numero possibile di società, società o divisioni. Si basano sui risultati esistenti di discipline statistiche, matematiche ed economiche (teoria dei giochi, accodamento, grafici, programmazione ottimale, statistiche matematiche).

Metodi di valutazione esperti

Questi metodi di ottimizzazione delle decisioni di gestione sono applicati quando il compito è parzialmente o completamente non soggetto a formalizzazione e la sua soluzione non può essere trovata per mezzo di metodi matematici.

La competenza è lo studio di questioni specifiche complesse nella fase di sviluppo di una decisione di gestione specifica da parte delle persone rilevanti che possiedono una speciale base di conoscenze e un'esperienza impressionante per ottenere conclusioni, raccomandazioni, opinioni, valutazioni. Nel processo di ricerca di esperti, gli ultimi risultati di scienza e tecnologia sono utilizzati come parte della specializzazione dell'esperto.

I metodi considerati di ottimizzazione di un certo numero di decisioni di gestione (valutazioni di esperti) sono efficaci nel risolvere i seguenti compiti di gestione nel settore produttivo:

1. Lo studio di processi complessi, fenomeni, situazioni, sistemi, che sono caratterizzati da caratteristiche qualitative non formalizzate.
2. Classificazione e determinazione secondo un determinato criterio di fattori significativi che sono decisivi per quanto riguarda il funzionamento e lo sviluppo del sistema di produzione.
3. I metodi di ottimizzazione considerati sono particolarmente efficaci nel campo della previsione delle tendenze di sviluppo del sistema di produzione, nonché della sua interazione con l'ambiente esterno.
4. Migliorare l'affidabilità delle valutazioni degli esperti si concentra principalmente sulle funzioni, che sono di natura quantitativa e qualitativa, facendo una media delle opinioni dei professionisti qualificati.

E questi sono solo alcuni dei metodi per ottimizzare un numero di decisioni di gestione (peer review).

Classificazione dei metodi considerati

I metodi per risolvere i problemi di ottimizzazione, in base al numero di parametri, possono essere suddivisi in:

• Metodi di ottimizzazione monodimensionale.
• I metodi di ottimizzazione sono multidimensionali.

Sono anche chiamati "metodi di ottimizzazione numerica". Per essere precisi, questi sono i suoi algoritmi di ricerca.

Nell'ambito dell'applicazione dei metodi derivati ​​sono:

• metodi di ottimizzazione diretta (ordine zero);
• metodi di sfumatura (1 ° ordine);
• metodi del secondo ordine, ecc.

La maggior parte dei metodi di ottimizzazione multidimensionale è vicina al problema del secondo gruppo di metodi (ottimizzazione unidimensionale).

Tecniche di ottimizzazione univariate

Qualsiasi metodo di ottimizzazione numerica si basa su un calcolo approssimativo o accurato delle sue caratteristiche, come i valori della funzione obiettivo e le funzioni che definiscono l'insieme ammissibile, i loro derivati. Pertanto, per ogni singola attività, la questione della scelta delle caratteristiche per il calcolo può essere risolta a seconda delle proprietà esistenti della funzione in questione, delle possibilità disponibili e dei limiti di archiviazione e elaborazione delle informazioni.

Esistono i seguenti metodi per risolvere i problemi di ottimizzazione (unidimensionale):

• Metodo di Fibonacci;
• dicotomia;
• sezione aurea;
• doppio passo.

Metodo di Fibonacci

Per prima cosa è necessario impostare le coordinate di t X sull'intervallo [a; b] come un numero uguale al rapporto tra la differenza (x - a) e la differenza (b - a). Pertanto, a ha un intervallo relativo [a; b] coordinata 0 e b - 1, punto medio ½.

Se supponiamo che F0 e F1 siano uguali tra loro e prendano il valore 1, F2 sarà uguale a 2, F3 - 3, ..., quindi Fn = Fn-1 + Fn-2. Quindi, Fn è il numero di Fibonacci, e la ricerca di Fibonacci è la strategia ottimale per la cosiddetta ricerca massima sequenziale perché è piuttosto strettamente correlata a loro.

Nell'ambito della strategia ottimale, è consuetudine scegliere xn - 1 = Fn - 2: Fn, xn = Fn - 1: Fn. Per uno dei due intervalli ([0; xn] o [xn - 1; 1]), ognuno dei quali può agire come un intervallo ristretto di incertezza, il punto (ereditato) relativo al nuovo intervallo avrà le coordinate [Fn - 3: Fn- 1] o [Fn - 2: Fn-1]. Inoltre, un punto è preso come xn - 2, che, rispetto al nuovo spazio, ha una delle coordinate presentate. Se usiamo F (xn - 2), il valore della funzione, che è ereditato dal gap precedente, diventa possibile ridurre l'intervallo di incertezza e trasmettere l'ereditarietà di un valore della funzione.

Alla fine, è possibile procedere a un tale intervallo di incertezza come [a; b], mentre il punto medio viene ereditato dal passaggio precedente. Come x1, viene impostato un punto che ha una coordinata relativa ½ + ε e l'intervallo di incertezza finale sarà [0, ½ + ε] o [½, 1] rispetto a [a; b].

Al primo passaggio, la lunghezza di questo intervallo è stata ridotta a Fn - 1: Fn (da uno). Nelle fasi finali, la riduzione delle lunghezze degli intervalli corrispondenti è rappresentata dai numeri Fn - 2: Fn - 1, Fn - 3: Fn - 2, ..., F2: F3, F1: F2 (1 + 2ε). Quindi, la lunghezza di un intervallo come la versione finale assumerà il valore (1 + 2ε): Fn.

Se trascuriamo ε, allora asintoticamente 1: Fn sarà uguale a rn, con n → ∞ e r = (√5 - 1): 2, che è approssimativamente uguale a 0.6180.

Va notato che asintoticamente per n significativi ogni passo successivo della ricerca di Fibonacci limita significativamente l'intervallo considerato con il coefficiente sopra menzionato. Questo risultato dovrebbe essere confrontato con 0,5 (coefficiente di restringimento dell'intervallo di incertezza nel quadro del metodo di bisezione per trovare la funzione zero).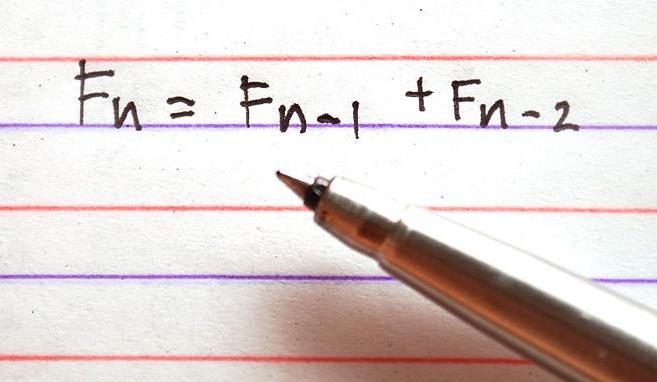

Metodo dicotomia

Se rappresentiamo una determinata funzione obiettivo, prima dobbiamo trovare il suo estremo nell'intervallo (a; b). Per fare ciò, l'asse delle ascisse è diviso in quattro parti equivalenti, quindi è necessario determinare il valore della funzione in questione a 5 punti. Quindi selezionare il minimo tra di loro. L'estremo della funzione deve trovarsi all'interno dell'intervallo (a '; b'), che è adiacente al punto minimo. I confini della ricerca sono ristretti 2 volte. E se il minimo si trova in M. A o b, viene ristretto quattro volte. Il nuovo intervallo è anche diviso in quattro segmenti uguali. A causa del fatto che i valori di questa funzione su tre punti sono stati determinati nella fase precedente, allora è necessario calcolare la funzione obiettivo in due punti.

Metodo della sezione aurea

Per valori significativi di n, le coordinate di tali punti come xn e xn - 1 sono vicine a 1 - r, pari a 0,3820 e r ≈ 0,6180. La spinta con questi valori è molto vicina alla strategia ottimale desiderata.

Se supponiamo che F (0,3820)> F (0,6180), allora l'intervallo [0; 0,6180] è delineato. Tuttavia, poiché 0.6180 * 0.6180 ≈ 0.3820 ≈ xn-1, allora a questo punto F è già noto. Di conseguenza, in ogni fase, a partire dal 2 °, è necessario un solo calcolo della funzione obiettivo, e ciascun passo riduce la lunghezza dell'intervallo considerato di un fattore di 0,6180.

A differenza della ricerca di Fibonacci, questo metodo non richiede il fissaggio del numero n anche prima che la ricerca abbia inizio.

La "sezione aurea" della sezione (a; b) è la sezione in cui il rapporto tra la lunghezza r e la parte più grande (a; c) è identico al rapporto tra la parte più grande di r e il più piccolo, cioè (a; c) a (c; b). Non è difficile immaginare che r sia determinato dalla formula sopra. Pertanto, con n significativo, il metodo di Fibonacci va in questo.

Metodo di raddoppio

L'essenza è la ricerca della direzione della diminuzione della funzione obiettivo, il movimento in questa direzione nel caso di una ricerca riuscita con un gradino gradualmente crescente.

Innanzitutto, determiniamo la coordinata iniziale M0 della funzione F (M), il valore minimo del passo h0, la direzione della ricerca. Quindi definiamo la funzione in m. Quindi, fai un passo e trova il valore di questa funzione a questo punto.

Se la funzione è inferiore al valore presente nel passaggio precedente, è necessario eseguire il passaggio successivo nella stessa direzione, dopo averlo aumentato in precedenza 2 volte. Quando il suo valore è maggiore di quello precedente, sarà necessario cambiare la direzione della ricerca, quindi iniziare a muoversi nella direzione selezionata con il passo h0. L'algoritmo presentato può essere modificato.

Metodi di ottimizzazione multidimensionale

Il suddetto metodo di ordine zero non tiene conto dei derivati ​​della funzione minimizzata, in modo che il loro utilizzo possa essere efficace in caso di difficoltà nel calcolo dei derivati.

Il gruppo di metodi del primo ordine è anche chiamato gradiente, perché il gradiente di questa funzione è usato per stabilire la direzione della ricerca - un vettore i cui componenti sono le derivate parziali della funzione minimizzata rispetto ai corrispondenti parametri ottimizzati.

Nel gruppo di metodi del 2 ° ordine vengono utilizzati 2 derivati ​​(il loro uso è piuttosto limitato a causa della presenza di difficoltà nel calcolarli).

Elenco dei metodi di ottimizzazione incondizionata

Quando si utilizza la ricerca multidimensionale senza l'uso di derivati, i metodi di ottimizzazione incondizionati sono i seguenti:

• Hook and Jeeves (implementazione di 2 tipi di ricerca - sul modello ed esplorazione);
• minimizzazione del simplex corretto (ricerca del punto minimo della funzione corrispondente confrontando ad ogni singola iterazione i suoi valori ai vertici del simplex);
• discesa ciclica delle coordinate (utilizzando i vettori delle coordinate come punti di riferimento);
• Rosenbrock (basato sull'uso della minimizzazione monodimensionale);
• minimizzazione da un simplex deformato (modifica del metodo di minimizzazione da un simplex regolare: aggiunta di una procedura di compressione, estensione).

Nella situazione dell'uso di derivati ​​nel processo di ricerca multidimensionale, si distingue il metodo di discesa più rapida (la procedura più fondamentale per minimizzare una funzione differenziabile con più variabili).

Distinguono anche questi metodi che usano direzioni coniugate (metodo Davidon-Fletcher-Powell). La sua essenza è la presentazione delle direzioni di ricerca come Dj * grad (f (y)).

Classificazione dei metodi di ottimizzazione matematica

Convenzionalmente, in base alla dimensione delle funzioni (obiettivo), sono:

• con 1 variabile;
• multidimensionale.

A seconda della funzione (lineare o non lineare), esiste un gran numero di metodi matematici volti a trovare un estremo per risolvere il problema.

In base al criterio di utilizzo dei derivati, i metodi di ottimizzazione matematica sono suddivisi in:

• metodi per calcolare 1 derivata della funzione obiettivo;
• multidimensionale (prima derivata - quantità vettoriale - gradiente).

Sulla base dell'efficienza del calcolo, ci sono:

• metodi di calcolo estremi rapidi;
• calcolo semplificato.

Questa è una classificazione condizionale dei metodi considerati.

Ottimizzazione dei processi aziendali

I metodi qui possono essere usati in modo diverso, a seconda dei problemi da risolvere. È consuetudine individuare i seguenti metodi per l'ottimizzazione dei processi di business:

• eccezioni (riduzione dei livelli di processo esistenti, eliminazione delle cause di interferenza e controllo degli input, riduzione delle rotte di trasporto);
• semplificazioni (facilitazione del passaggio dell'ordine, riduzione della complessità della struttura del prodotto, distribuzione del lavoro);
• standardizzazione (uso di programmi speciali, metodi, tecnologie, ecc.);
• accelerazione (ingegneria parallela, stimolazione, progettazione operativa di prototipi, automazione);
• cambiamento (cambiamenti nel campo delle materie prime, tecnologie, metodi di lavoro, posizione del personale, sistemi di lavoro, quantità di ordine, procedura di elaborazione);
• assicurare l'interoperabilità (in termini di unità organizzative, personale, sistema di lavoro);
• selezione e inclusione (per quanto riguarda i processi, i componenti necessari).

Ottimizzazione fiscale: metodi

La legislazione russa offre al contribuente possibilità molto ricche per ridurre l'ammontare delle imposte, motivo per cui è consuetudine individuare tali metodi volti a minimizzarli, come quelli generali (classici) e speciali.

I metodi generali di ottimizzazione fiscale sono i seguenti:

• elaborazione della politica contabile della società con il massimo utilizzo possibile delle opportunità offerte dalla legislazione russa (la procedura per la cancellazione dell'IBE, la scelta del metodo di calcolo delle entrate dalla vendita di beni, ecc.);
• ottimizzazione mediante contratto (conclusione di transazioni privilegiate, uso chiaro e competente della formulazione, ecc.);
• l'uso di vari tipi di benefici, esenzioni fiscali.

Il secondo gruppo di metodi può essere utilizzato anche da tutte le imprese, ma hanno comunque un ambito abbastanza ristretto. I metodi speciali di ottimizzazione fiscale sono i seguenti:

• sostituzione delle relazioni (l'operazione, che prevede una tassazione onerosa, è sostituita da un'altra, che consente di raggiungere un obiettivo simile, ma allo stesso tempo utilizzare una procedura di tassazione preferenziale).
• separazione delle relazioni (sostituzione solo di una parte di una transazione commerciale);
• differimento del pagamento delle imposte (posticipando il momento di accadimento oggetto tassabile per un altro periodo di calendario);
• riduzione diretta dell'oggetto tassabile (eliminazione di molte transazioni o proprietà imponibili senza avere un impatto negativo sulla principale attività economica dell'azienda).