Di cosa si tratta - un cono in geometria. Cono dritto con base rotonda e sue caratteristiche

La geometria spaziale, il cui svolgimento si svolge al liceo, esamina le caratteristiche e le proprietà di varie forme geometriche in tre dimensioni. Una di queste figure conosciute è il cono. Che questo è un cono, quali elementi descrive e quali proprietà possiede, l'articolo risponderà a queste domande.

Cono in geometria

Dal punto di vista della stereometria, un cono è una figura formata nello spazio collegando segmenti retti di un certo punto con una curva in un piano. Questa curva è chiamata una direttrice o una guida. Limita la forma della base. Una direttrice può essere una linea chiusa, come un'ellisse o un cerchio, o potrebbe non essere chiusa, come un'iperbole o una parabola. Tutti i segmenti che collegano la direttrice al punto di spazio sopra menzionato sono chiamati generatori o generatori. L'insieme di generatori definisce una superficie conica e il punto da cui escono è chiamato il vertice del cono.

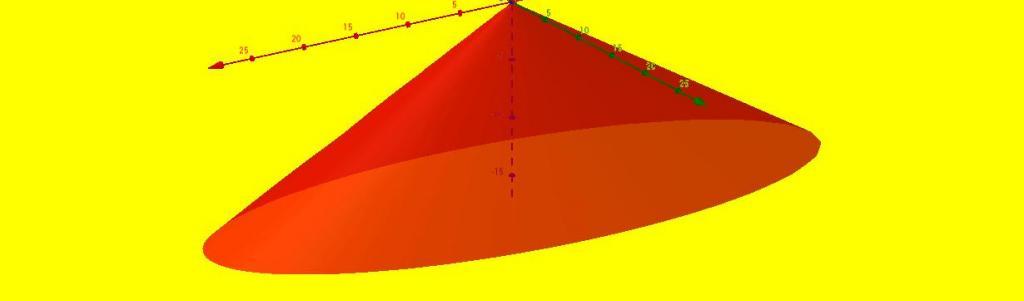
Quindi, un cono è una figura che ha un vertice, senza bordi e consiste di due superfici (una base piatta e una superficie conica laterale). Il cono ellittico è mostrato nella figura sopra.

Cono circolare o rotondo

Sotto la parola "round" nel titolo dell'articolo capisci la figura, la cui base è un cerchio. A differenza di altri tipi di cono, è possibile ottenere una cifra tonda come risultato della rotazione. La figura seguente mostra questo processo.

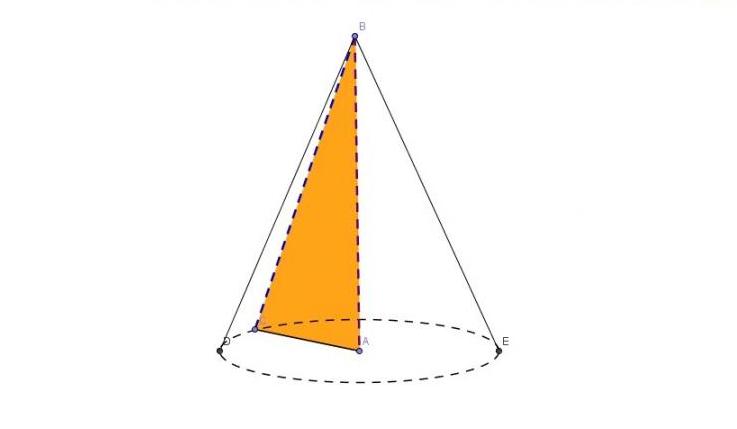
Spieghiamo brevemente cosa mostra la figura. Il triangolo ABC è rettangolare. Se viene ruotato attorno alla gamba AB, la gamba AC descriverà una superficie del cono, la base e l'ipotenusa BC provocheranno la formazione di una superficie conica come risultato della rotazione.

Il cono mostrato nella figura non è solo rotondo, ma anche dritto. Quest'ultima proprietà è importante da considerare quando si eseguono calcoli di parametri lineari, area e volume della figura.

La forma geometrica di un cono è lineare se l'altezza h cade esattamente al centro della base (in questo caso l'altezza è il segmento AB e il centro della base è il punto A). Se la condizione specificata non viene soddisfatta, la figura viene chiamata obliqua. I coni obliqui e diritti sono mostrati sotto per chiarezza.

Molti oggetti che ci circondano, come coni gelato, un cono stradale a strisce o un imbuto per versare il liquido attraverso le aperture strette, hanno una forma a cono con una base rotonda.

Successivamente, consideriamo le caratteristiche quantitative di un cono diritto con una base rotonda.

Le dimensioni lineari della figura e l'angolo alla base

Le dimensioni lineari di un cono sono un insieme di parametri che consentono di definire in modo univoco una figura nello spazio. Sono i seguenti:

• raggio di base r;
• altezza h;
• generatrice g.

Si noti che per il tipo di cono in esame tutte le generatrici sono uguali tra loro e intersecano la base della figura con lo stesso angolo.

Oltre ai suddetti parametri lineari, il cono è anche caratterizzato dall'angolo φ tra generatore e base.

Tutte queste caratteristiche sono correlate l'una con l'altra dalle seguenti equazioni di base:

g = √ (h ² + r ² );

g = h / sin (φ);

g = r / cos (φ);

h = r * tg (φ)

Queste uguaglianze possono essere scritte indipendentemente se consideriamo un triangolo rettangolo all'interno del cono e richiamiamo le definizioni delle funzioni trigonometriche indicate.

Superficie

L'area della base e la superficie conica sono una caratteristica importante del cono. È più chiaro e più facile studiare la superficie di una figura non in tridimensionale, ma nello spazio bidimensionale. Per fare ciò, crea i cosiddetti modelli di scansione. Potete immaginare il processo della sua ricevuta come segue: Supponiamo che ci sia un cono di carta. Per prima cosa, abbiamo tagliato la sua base lungo la circonferenza, quindi abbiamo tagliato la superficie conica lungo il generatore e lo abbiamo aperto. Abbiamo ricevuto una scansione del cono, che è mostrato sotto nella figura.

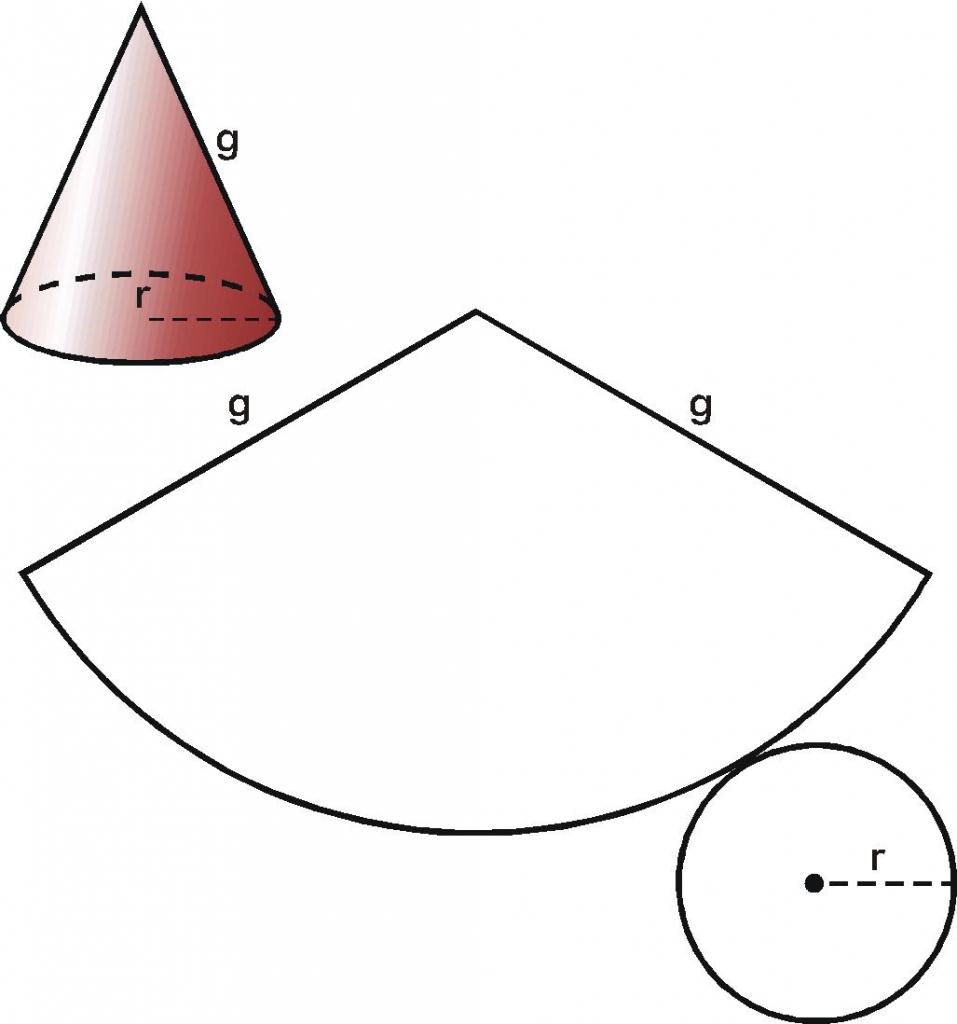
L'area dell'intero sweep S è uguale a:

S = S _o + S _b

Dove il primo termine (S _o ) è l'area di un cerchio, il secondo termine (S _b ) è l'area di un settore circolare che riflette una superficie conica. Il valore di S _{o viene} calcolato dalla seguente formula:

S _o = pi * r ²

Con un settore circolare, la situazione è più complicata. È delimitato da due raggi la cui lunghezza è uguale alla generatrice g e un arco corrispondente alla circonferenza del cerchio di base. Questa informazione numerica consente di determinare in modo univoco l'area del settore. Non entreremo nei calcoli matematici, ma daremo immediatamente la formula finale per S _b :

S _b = pi * r * g

Il confronto delle formule scritte per S _b e S _o suggerisce che l'area della superficie laterale è sempre maggiore di quella per la base per g / r.

La formula per la superficie totale è la seguente:

S = pi * r * (r + g)

Dimensione del corpo

Un cono è una figura spaziale, quindi ha un certo volume. Corrisponde numericamente all'area dello spazio che è delimitata da una superficie conica e da una base circolare. Per determinare il volume del cono, utilizzare la seguente espressione:

V = 1/3 * S _o * h

Sostituendo in questa espressione la formula per S _o , otteniamo:

V = 1/3 * pi * r ² * h

Alcuni lettori potrebbero aver notato che la formula del volume del cono corrisponde a quella della piramide. Questa coincidenza non è casuale, poiché le forme di queste figure diventano identiche se il numero di bordi di una linea retta della piramide aumenta all'infinito.