Processo adiabatico, sua essenza e formule

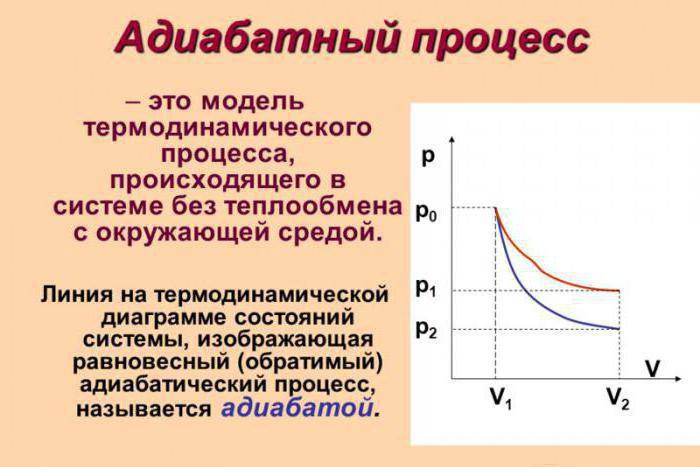
Il processo adiabatico (indicato come adiabatico in alcune fonti) è un processo termodinamico che si verifica in assenza di scambio di calore con l'ambiente. Ci sono diversi fattori che caratterizzano questa classe. Ad esempio, il processo adiabatico si verifica in modo dinamico e viene impostato in un breve periodo di tempo. Ci sono processi di questa classe, di regola, all'istante.

Connessione con la prima legge della termodinamica

Il processo adiabatico (adiabatico) può essere direttamente collegato a primo principio della termodinamica. La dicitura "di default" si legge come segue: un cambiamento nella quantità di calore nel sistema durante un processo termodinamico in esso sarà numericamente uguale alla somma del cambiamento nell'energia interna del gas ideale e il lavoro svolto da questo gas.

Se proviamo a scrivere primo avvio della termodinamica nella sua forma standard, otteniamo la seguente espressione: dQ = dU + dA. E ora proveremo a modificare questa formula con riferimento al processo adiabatico. Come accennato in precedenza, tali processi avvengono sotto la condizione dell'assenza di scambio di calore con l'ambiente circostante (esterno, come alcune fonti letterarie lo chiamano).

In questo caso, la formula che descrive la prima legge della termodinamica avrà la seguente forma: dA = -dU. Ora un po 'di più sulla modifica. Se diciamo che non c'è scambio di calore nel sistema, la variazione della quantità di calore (indicata nella formula della prima legge della termodinamica per dQ) sarà zero. Di conseguenza, possiamo trasferire uno degli addendi dalla destra alla sinistra, dopo di che otteniamo la formula ridotta alla forma descritta in precedenza.

Corollario della prima legge della termodinamica per il processo adiabatico

Supponiamo che si sia verificato un processo adiabatico nel sistema. In questo caso, è possibile, senza entrare nei più piccoli dettagli, dire che il gas fa il lavoro durante l'espansione, ma allo stesso tempo perde la sua energia interna. In altre parole, il lavoro svolto durante l'espansione adiabatica del gas verrà effettuato a causa della perdita di energia interna. Di conseguenza, come risultato di questo processo, prenderemo in considerazione una diminuzione della temperatura della sostanza stessa.

È assolutamente logico supporre che se il gas viene compresso adiabaticamente, la sua temperatura aumenterà. È facile vedere che durante il processo tutte le principali caratteristiche di un gas ideale cambieranno. Riguarda la sua pressione, il volume e la temperatura. Pertanto, il nome del processo adiabatico da parte dell'isoprocesso è diventato un errore grossolano.

Processo adiabatico. formula

La formula derivata dalla prima legge della termodinamica è stata trascritta in precedenza. Usandolo, possiamo facilmente calcolare il lavoro in generale, che il gas eseguirà durante il processo adiabatico. Come avrai intuito, lo faremo con l'aiuto dell'integrazione.

Quindi, al fine di ottenere la formula generale per il lavoro per x moli di gas, integriamo l'espressione della prima legge della termodinamica per un processo adiabatico. Tutto questo assomiglierà a questo: A = - (integrale) di dU. Apriamo questa espressione, otteniamo: A = - xCv (integrale da T1 a T2) dT.

Ora che abbiamo portato l'integrale in una forma finita, possiamo semplificarlo. All'uscita otteniamo la seguente formula: A = - xCv (T2 - T1). Bene, l'ultimo passo sarà una leggera semplificazione. Ci liberiamo del meno prima della formula. Per fare questo, facciamo una piccola permutazione tra parentesi, cambiando la temperatura finale con le posizioni iniziali. Di conseguenza, otteniamo: A = xCv (T1 - T2).

Equazione adiabatica

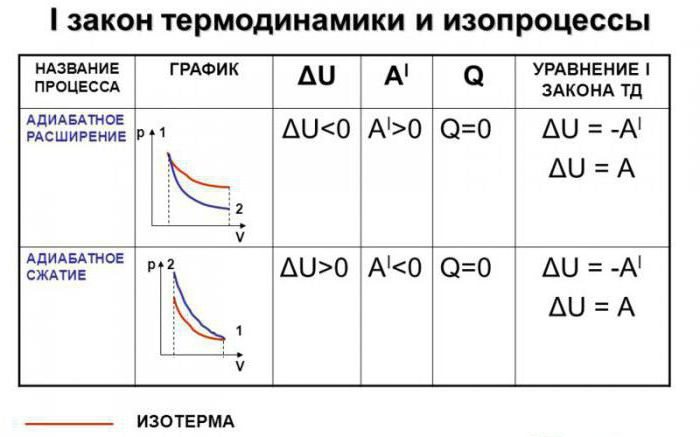
Usando la prima legge della termodinamica per un processo adiabatico, possiamo trovare l'equazione adiabatica. Allo stesso tempo, verrà registrato per un numero arbitrario di moli di un gas ideale. Quindi, scriviamo la formula originale. Assomiglia a questo: dA + dU = 0. Ma sappiamo perfettamente che il lavoro di un gas ideale non è numericamente altro che il prodotto della pressione e del cambiamento di volume.

Allo stesso tempo cambia energia interna sarà uguale al lavoro svolto con il segno opposto. E l'abbiamo già trovato con l'aiuto dell'integrazione. Quindi, la prima legge della termodinamica per il processo adiabatico può assumere la forma seguente: pdV + xCvdT = 0. Dobbiamo escludere un indicatore da questa equazione, cioè la temperatura. Piuttosto, i suoi cambiamenti. Per fare questo, ci rivolgiamo all'equazione che è abbastanza spesso usata nella fisica molecolare. Vale a dire, l'equazione di Mendeleev-Clapeyron.

Espressione primaria

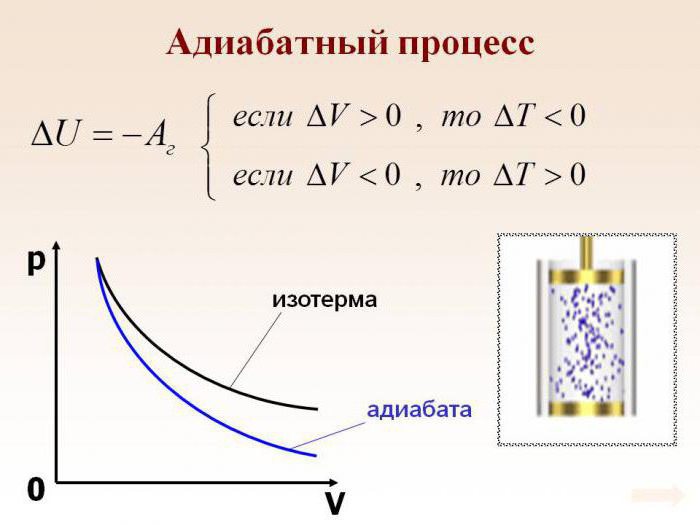
Dobbiamo differenziarlo, cosa che faremo. Quindi, in generale, l'equazione è la seguente: PV = XRT. A causa della differenziazione, sarà ridotto alla seguente forma: pdV + Vdp = xRdT. Da qui possiamo esprimere il cambiamento di energia. Sarà uguale alla parte sinistra divisa per il prodotto della quantità di una sostanza e la costante universale del gas. In altre parole, la formula sarebbe: (pdV + Vdp) / xR. Resta solo da semplificare. Di conseguenza, otteniamo la seguente espressione: dT = (pdV + Vdp) / x (Cp - Cv)

In effetti, la prima parte del compito è completata. Resta solo da portare tutto in mente.

Espressione secondaria Sostituzione del valore

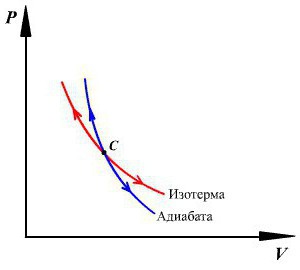
Prendiamo la formula di Mendeleev-Clapeyron ottenuta come risultato della differenziazione e la sostituiamo nell'espressione che abbiamo derivato in precedenza per la prima legge della termodinamica rispetto al processo adiabatico. Quindi cosa otteniamo? Tutta questa espressione macchinosa prende la seguente forma: pdV + xCv ((pdV + Vdp) / x (Cp-Cv)) = 0.

Per semplificare tutto questo, dobbiamo prendere in considerazione un paio di fatti. Innanzitutto, l'espressione può essere semplificata riducendola a un denominatore comune. Quando otteniamo una frazione, possiamo usare la buona vecchia regola, che dice che una frazione è zero quando il suo numeratore è zero e il denominatore è diverso da zero. Come risultato della combinazione di tutte queste azioni, otteniamo la seguente espressione: pCpdV - pCvdV + pCvdV + VCvdp = 0.

Ora il passo successivo è dividere questa espressione in pVCv. Otteniamo la somma di due parti, dando come risultato zero. Questo sarà Cp / Cv * dV / V + dp / p = 0. Questa formula deve essere integrata. Quindi otteniamo la seguente espressione: y (integrale) dV / V + (integrale) dp / p = (integrale) 0.

Bene, allora tutto è abbastanza semplice. Usando le formule di integrazione (le integrali di tabella possono essere utilizzate per rendere tutto più semplice), otteniamo la seguente voce: y ln V + ln p = ln (const). Risulta che p (V) y = const. Nella fisica molecolare, questa espressione è chiamata equazione di Poisson. Molte fonti scientifiche chiamano anche questa formula l'equazione adiabatica. Allo stesso tempo, il valore di y, che si trova in questo record, è chiamato indice adiabatico. È uguale a (i + 2) / i. Va notato che l'indice adiabatico è sempre maggiore di uno, il che, in linea di principio, è logico.

Esempi di processi adiabatici

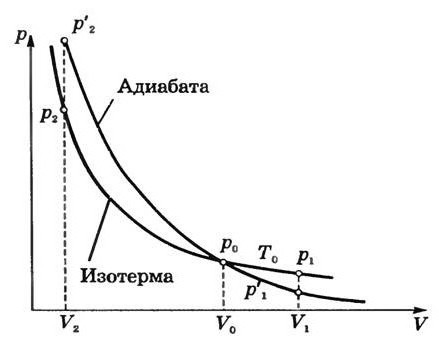
Poco dopo la scoperta del processo adiabatico, iniziò un enorme numero di studi diversi. Pertanto, è stato creato il primo modello teorico correlato al ciclo di Carnot. Fu lei che permise l'instaurazione di limiti condizionati che limitarono lo sviluppo dei motori termici. Ma nel caso di alcuni processi reali da eseguire Ciclo di Carnot abbastanza difficile. Il fatto è che consiste di isoterme. E, a loro volta, richiedono l'impostazione di un certo tasso di processi termodinamici.

conclusione

Per aggirare tali problemi, è stato inventato il ciclo Otto, così come il ciclo liquefazione del gas. Sono stati ampiamente utilizzati nella risoluzione di problemi specifici nella pratica. Gli studi iniziali hanno mostrato la possibilità di descrivere alcuni processi naturali nel piano adiabatico, che hanno permesso di identificare gli schemi generali dei processi corrispondenti. Un esempio di processo adiabatico può essere chiamato una reazione chimica che si verifica all'interno di un certo volume di gas, se il sistema è chiuso e non c'è scambio di calore con l'ambiente esterno.