Tutte le opzioni su come trovare l'area trapezoidale
Trapezoidale a molti lati ... Può essere arbitrario, isoscele o rettangolare. E in ogni caso, è necessario sapere come trovare l'area del trapezio. Naturalmente, il modo più semplice per ricordare le formule di base. Ma a volte è più facile usare quello derivato con tutte le caratteristiche di un particolare forma geometrica.
Qualche parola sul trapezio e sui suoi elementi
Qualsiasi quadrangolo i cui due lati sono paralleli può essere chiamato trapezio. In generale, non sono uguali e sono chiamati basi. Il più grande di loro è più basso, e l'altro è superiore.
Gli altri due lati sono laterali. Per un trapezio arbitrario, hanno lunghezze diverse. Se sono uguali, la cifra diventa isoscele.
Se improvvisamente l'angolo tra i lati e la base è di 90 gradi, il trapezio è rettangolare.
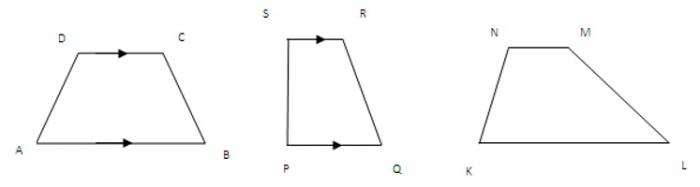
Tutte queste caratteristiche possono aiutare a risolvere il problema di come trovare l'area di un trapezio.
Tra gli elementi della figura che possono essere indispensabili nella risoluzione dei problemi, possiamo evidenziare quanto segue:
- altezza, cioè un segmento perpendicolare ad entrambe le basi;
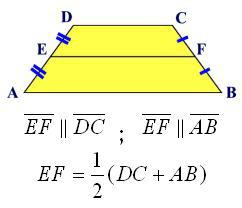
- la linea di mezzo, che ha alle estremità i lati centrali.
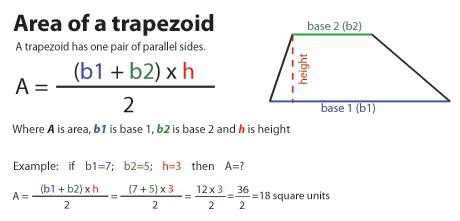
Con quale formula calcolare l'area, se conosci la base e l'altezza?
Questa espressione è data dal principale, perché molto spesso è possibile riconoscere questi valori, anche quando non sono esplicitamente indicati. Quindi, per capire come trovare area del trapezio dovrai piegare entrambe le basi e dividerle in due. Il valore risultante viene quindi moltiplicato per il valore di altezza.
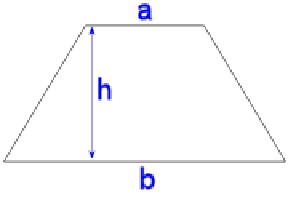
Se denotiamo le basi con le lettere 1 e 2 , l'altezza è n, quindi la formula per l'area sarà simile a questa:
S = ((a 1 + a 2 ) / 2) * n.
La formula per calcolare l'area, se data la sua altezza e la linea di mezzo
Se si osserva attentamente la formula precedente, è facile vedere che il valore della linea media è chiaramente presente in esso. Vale a dire, la somma delle basi divisa per due. Lascia che la linea di mezzo sia designata dalla lettera l, quindi la formula per l'area sarà così:
Ad
S = l * n.
La capacità di trovare l'area in diagonale
Questo metodo ti aiuterà se conosci l'angolo formato da loro. Supponiamo che le diagonali siano denotate dalle lettere q 1 e g 2 , e che gli angoli tra loro siano α e β. Quindi la formula per trovare l'area di un trapezio sarà scritta come segue:
S = ((d 1 * d 2 ) / 2) * sin α.
In questa espressione, puoi facilmente sostituire α con β. Il risultato non cambierà.
Come scoprire l'area se sono noti tutti i lati della figura?
Ci sono anche situazioni in cui sono esattamente i lati che sono noti in questa figura. Questa formula è macchinosa e difficile da ricordare. Ma è possibile. Lascia che i lati abbiano la designazione: in 1 e 2 , la base e 1 più di un 2 . Quindi la formula dell'area sarà simile a questa:
Ad
S = ((a 1 + a 2 ) / 2) * √ {in 1 2 - [(a 1 - a 2 ) 2 + in 1 2 - in 2 2 ) / (2 * (a 1 - a 2 )) ] 2 }.
Modi per calcolare l'area di un trapezio isoscele
Il primo è legato al fatto che un cerchio può essere inserito in esso. E, conoscendo il suo raggio (è indicato dalla lettera r), così come l'angolo alla base - γ, puoi usare la seguente formula:
S = (4 * r 2 ) / sin γ.
Quest'ultima formula generale, che si basa sulla conoscenza di tutti i lati della figura, sarà notevolmente semplificata dal fatto che le parti hanno lo stesso significato:
S = ((a 1 + a 2 ) / 2) * √ {in 2 - [(a 1 - a 2 ) 2 / (2 * (a 1 - a 2 ))] 2 }.
Metodi per calcolare l'area di un trapezio rettangolare
È chiaro che qualsiasi cosa elencata per una forma arbitraria andrà bene. Ma a volte è utile conoscere una caratteristica di tale trapezio. Sta nel fatto che la differenza nei quadrati delle lunghezze delle diagonali è uguale alla differenza composta dai quadrati delle basi.
Ad
Spesso, le formule per un trapezio vengono dimenticate, mentre vengono ricordate le espressioni per le aree di un rettangolo e di un triangolo. Quindi puoi applicare un modo semplice. Dividere il trapezio in due forme, se è rettangolare o tre. Uno sarà esattamente un rettangolo e il secondo, o due restanti, triangoli. Dopo aver calcolato le aree di queste figure le aggiungeremo solo.
Questo è un modo abbastanza semplice di come trovare quadrato trapezio.
Cosa succede se le coordinate dei vertici del trapezio sono note?
In questo caso, dovrai usare un'espressione che ti permetta di determinare la distanza tra i punti. Può essere applicato tre volte: per imparare sia le basi che l'altezza. E poi basta applicare la prima formula, che è descritta un po 'più in alto.
Per illustrare questo metodo, puoi fare un esempio. Dati i vertici con le coordinate A (5; 7), B (8; 7), C (10; 1), D (1; 1). Hai bisogno di conoscere l'area della figura.
Prima di trovare l'area di un trapezio, è necessario calcolare le lunghezze di base per coordinate. Avrai bisogno della seguente formula:
lunghezza del segmento = √ {(differenza delle prime coordinate dei punti) 2 + (differenza delle seconde coordinate dei punti) 2 }.
La base superiore è designata AB, il che significa che la sua lunghezza sarà uguale a √ {(8-5) 2 + (7-7) 2 } = √9 = 3. Quello inferiore sarà SD = √ {(10-1) 2 + (1-1 ) 2 } = √81 = 9.
Ora devi tenere l'altezza dalla cima alla base. Sia il suo inizio al punto A. La fine del segmento sarà sulla base inferiore nel punto con le coordinate (5; 1), sia il punto N. La lunghezza del segmento AN sarà uguale a √ {(5-5) 2 + (7-1) 2 } = √36 = 6.
Ad
Resta solo da sostituire i valori risultanti nella formula dell'area trapezoidale:
S = ((3 + 9) / 2) * 6 = 36.
Il problema è risolto senza unità, poiché la scala della griglia delle coordinate non è specificata. Può essere un millimetro o un metro.
Esempi di compiti
№ 1. Condizione. Angolo noto tra le diagonali di un trapezio arbitrario, è pari a 30 gradi. La diagonale più piccola è di 3 dm, e la seconda è 2 volte più grande. È necessario calcolare l'area del trapezio.
La decisione Per prima cosa devi sapere la lunghezza della seconda diagonale, perché senza questo non puoi contare la risposta. Calcola è facile, 3 * 2 = 6 (dm).
Ora è necessario utilizzare la formula appropriata per l'area:
S = ((3 * 6) / 2) * sin 30º = 18/2 * ½ = 4,5 (dm 2 ). Problema risolto
Risposta: l' area del trapezio è di 4,5 dm 2 .
№ 2. Condizione. Nel trapezio dell'AVSD, le basi sono i segmenti AD e BC. Il punto E è il centro del lato della SD. Da esso, perpendicolare alla retta AB viene disegnata, la fine di questo segmento è indicata dalla lettera N. È noto che le lunghezze AB ed EH sono rispettivamente 5 e 4 cm. È necessario calcolare l'area del trapezio.
Ad
La decisione Per prima cosa devi fare un disegno. Poiché il valore della perpendicolare è più piccolo del lato a cui è condotto, il trapezio sarà leggermente esteso verso l'alto. Quindi EN sarà all'interno della figura.
Per vedere chiaramente lo stato di avanzamento dell'attività, è necessario eseguire ulteriori costruzioni. Vale a dire, disegnare una linea retta che sarà parallela al lato AB. I punti di intersezione di questa linea con AD - P e con la continuazione delle forze armate - X. La figura risultante è il parallelogramma. Inoltre, la sua area è uguale a quella desiderata. Ciò è dovuto al fatto che i triangoli che si sono rivelati con la costruzione aggiuntiva sono uguali. Ciò segue dall'uguaglianza del lato e dei due angoli adiacenti ad esso, uno - verticale, l'altro - che giace trasversalmente.
Per trovare l'area del parallelogramma è possibile con la formula, che contiene il prodotto del lato e dell'altezza, abbassato su di esso.
Quindi, l'area del trapezio è 5 * 4 = 20 cm 2 .
Risposta: S = 20 cm 2 .
№ 3. Condizione. Gli elementi di un trapezio isoscele hanno i seguenti significati: la base inferiore è di 14 cm, la parte superiore è di 4 cm e l'angolo acuto è di 45º. È necessario calcolare la sua area.
La decisione Lascia che la base più piccola sia designata come BC. L'altitudine tracciata dal punto B sarà chiamata HV. Poiché l'angolo è 45º, il triangolo ABH sarà rettangolare e isoscele. Quindi AN = BH. Inoltre, NA è molto facile da trovare. È uguale alla metà della differenza di base. Cioè (14 - 4) / 2 = 10/2 = 5 (cm).
I motivi sono noti, conteggiati in altezza. Puoi usare la prima formula, che è stata considerata qui per un trapezio arbitrario.
S = ((14 + 4) / 2) * 5 = 18/2 * 5 = 9 * 5 = 45 (cm 2 ).
Risposta: l' area richiesta è di 45 cm 2 .
№ 4. Condizione. C'è un arbitrario trapezio AVSD. Sui suoi lati, i punti O ed E sono presi, in modo che l'OE sia parallelo alla base dell'arca. L'area del trapezio AOED è cinque volte più grande di quella del CFE. Calcola il valore OE se le lunghezze di base sono note.
La decisione Sarà necessario tracciare due linee rette parallele AB: il primo attraverso il punto C, la sua intersezione con OE è il punto T; il secondo attraverso E e il punto di intersezione con AD sarà M.
Lascia lo sconosciuto OE = x. L'altezza del trapezio più piccolo del CFE è n 1 ;
Poiché le aree di questi due trapezi sono correlate da 1 a 5, possiamo scrivere la seguente uguaglianza:
(x + a 2 ) * n 1 = 1/5 (x + a 1 ) * n 2
o
n 1 / n 2 = (x + a 1 ) / (5 (x + a 2 )).
Le altezze e i lati dei triangoli sono proporzionali per costruzione. Pertanto, possiamo scrivere un'altra uguaglianza:
n 1 / n 2 = (x - a 2 ) / (a 1 - x).
Nelle ultime due voci sul lato sinistro ci sono valori uguali, quindi puoi scrivere che (x + a 1 ) / (5 (x + a 2 )) è uguale a (x - a 2 ) / (a 1 - x).
Ciò richiede una serie di trasformazioni. Prima moltiplicare in senso trasversale. Appariranno delle parentesi che indicano la differenza dei quadrati. Dopo aver applicato questa formula, otterrai una breve equazione.
È necessario aprire le parentesi e spostare tutti i termini dallo sconosciuto "x" sul lato sinistro e quindi estrarre radice quadrata.
Risposta : x = √ {(a 1 2 + 5 a 2 2 ) / 6}.