Tutte le sottigliezze su come calcolare l'area del parallelepipedo
Il parallelepipedo è la figura più comune tra coloro che circondano le persone. La maggior parte delle premesse sono sue. È particolarmente importante conoscere l'area del parallelepipedo, almeno le sue facce laterali, durante la riparazione. Dopotutto, è necessario sapere esattamente quanto materiale acquistare.
Com'è?
Questo è un prisma con una base quadrangolare. Pertanto, ha quattro facce laterali che sono parallelogrammi. Cioè, un corpo del genere ha solo 6 facce.
Per determinare il parallelepipedo nello spazio, determina l'area e il volume. Il primo può essere sia separatamente per ogni faccia che per l'intera superficie. Inoltre, emettono più e solo le facce laterali.
Quali sono i tipi di parallelepipedi?
Inclinato. Uno in cui le facce laterali formano un angolo con la base che è diverso da 90 gradi. I suoi quadrilateri superiore e inferiore non si trovano l'uno di fronte all'altro, ma sono spostati.
Ad
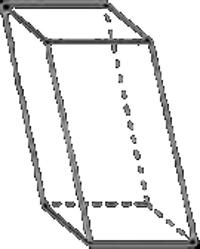
Direct. Un parallelepipedo, le cui facce laterali sono rettangoli, e alla base giace una figura con angoli arbitrari.
Rettangolare. Un caso speciale del tipo precedente: nella sua base è un rettangolo.
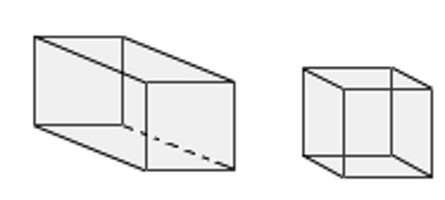
Cube. Un tipo speciale di parallelepipedo in cui tutte le facce sono rappresentate da quadrati.
Alcune caratteristiche matematiche del parallelepipedo
Una situazione può sorgere quando sono utili nel trovare l'area parallelepipeda.
- I bordi che si trovano uno di fronte all'altro non sono solo paralleli, ma uguali.
- La diagonale del punto di intersezione parallelepipedo è divisa in parti uguali.
- In un caso più generale, se un segmento collega due punti sulla superficie del corpo e passa attraverso il punto di intersezione delle diagonali, allora è diviso a metà da questo punto.
- Per un parallelepipedo rettangolare, l'uguaglianza è valida, in cui in una parte c'è un quadrato della diagonale, e nell'altra - la somma dei quadrati della sua altezza, larghezza e lunghezza.
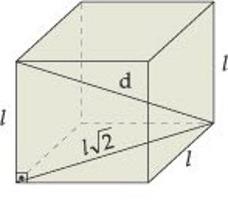
Quadrato parallelepipedo
Se denotiamo l'altezza del corpo come "n" e il perimetro di base con la lettera Р oc , allora l'intera superficie laterale può essere calcolata con la formula:
Lato S = P oc * n
Usando questa formula e determinando l'area della base, possiamo contare l'area totale:
S = lato S + 2 * S oc
Nell'ultima voce S oc ., Cioè, l'area della base del parallelepipedo, può essere calcolata dalla formula per il parallelogramma. In altre parole, hai bisogno di un'espressione in cui devi moltiplicare il lato e l'altezza calata su di esso.
Ad

Quadrato parallelepipedo
Viene adottata la designazione standard della lunghezza, larghezza e altezza di un tale corpo con le lettere "a", "b" e "c", rispettivamente. L'area della superficie laterale sarà espressa dalla formula:
Lato S = 2 * s * (a + b)
Per calcolare l'area totale di un parallelepipedo rettangolare, abbiamo bisogno della seguente espressione:
S = 2 * (aw + bs + as)
Se risulta necessario conoscere l'area della sua base, è sufficiente ricordare che questo è un rettangolo, il che significa che è sufficiente moltiplicare "a" e "c".
Cubo quadrato
La sua superficie laterale è formata da quattro quadrati. Quindi, per trovarlo, è necessario utilizzare la formula ben nota per il quadrato e moltiplicarla per quattro.
Lato S = 4 * a 2
E a causa del fatto che le sue basi sono gli stessi quadrati, l'area totale è determinata dalla formula:
S = 6 * a 2

Piazze inclinate a parallelepipedo
Poiché i suoi volti sono parallelogrammi, devi scoprire l'area di ciascuno di essi e poi piegarlo. Fortunatamente, il contrario è uguale. Pertanto, è necessario calcolare l'area solo tre volte e quindi moltiplicarle per due. Se lo scrivi sotto forma di formula, ottieni quanto segue:
Ad
Lato S = (S 1 + S 2 ) * 2,
S = (S 1 + S 2 + S 3 ) * 2
Qui, S 1 e S 2 sono le aree di due facce laterali e S 3 sono basi.
Attività correlate
Il primo compito. Condizioni. Hai bisogno di sapere la lunghezza cubo diagonale, se l'area della sua intera superficie è di 200 mm 2 .
La decisione Dobbiamo iniziare ottenendo un'espressione per il valore desiderato. Il suo quadrato è uguale a tre quadrati del lato del cubo. Ciò significa che la diagonale è uguale a "a" moltiplicata per la radice di 3.
Ma il lato del cubo è sconosciuto. Qui dovrai approfittare del fatto che l'intera superficie è conosciuta. Dalla formula risulta che "a" è uguale a radice quadrata da S privato e 6.
Resta solo da contare. Il bordo del cubo è √ (200/6), che è 10 / √3 (mm). Quindi la diagonale sarà uguale a (10 / √3) * √3 = 10 (mm).
La risposta è La diagonale del cubo è 10 mm.
Il secondo compito. Condizioni. Bisogno di calcolare superficie del cubo, se si sa che il suo volume è 343 cm 2 .
La decisione Dovrai utilizzare la stessa formula per l'area del cubo. Di nuovo, è di nuovo un bordo sconosciuto del corpo. Ma dato il volume. Dalla formula per il cubo è molto facile imparare "a". Sarà uguale a radice cubica di 343. Un semplice calcolo fornisce il valore per il bordo: a = 7 cm.
Ad
Ora resta da contare il suo quadrato e moltiplicare per 6. a 2 = 7 2 = 49, quindi l'area sarà pari a 49 * 6 = 294 (cm 2 ).
La risposta è S = 294 cm 2 .
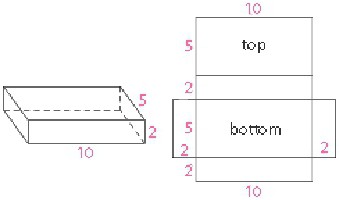
Il terzo compito. Condizioni. Viene fornito un prisma quadrangolare regolare con una base di 20 dm. È necessario trovare il suo bordo laterale. È noto che l'area parallelepipeda è pari a 1760 dm 2 .
La decisione Inizia il ragionamento con la formula per l'area dell'intera superficie del corpo. Solo in essa è necessario considerare che i bordi "a" e "b" sono uguali. Questo deriva dall'affermazione che il prisma è corretto. Quindi, alla sua base si trova un quadrilatero con lati uguali. Quindi a = c = 20 dm.
Data questa circostanza, la formula dell'area è semplificata a questo:
S = 2 * (a 2 + 2c).
In esso, tutto è noto, ad eccezione del valore desiderato "c", che è precisamente il bordo laterale del parallelepipedo. Per trovarlo, è necessario eseguire la conversione:
- dividere tutte le disuguaglianze di 2;
- quindi sposta i termini in modo che la sinistra sia 2a, e sulla destra l'area divisa per 2 e il quadrato "a", quest'ultima contrassegnata con "-";
- quindi dividi l'uguaglianza di 2a.
Il risultato è l'espressione:
c = (s / 2 - a 2 ) / (2a)
Dopo aver sostituito tutti i valori noti e aver eseguito azioni, risulta che il bordo laterale è uguale a 12 dm.
La risposta è Il bordo laterale "c" è 12 dm.
Il quarto compito. Condizioni. Dato un parallelepipedo rettangolare. Una delle sue facce ha un'area di 12 cm 2 . È necessario calcolare la lunghezza del bordo, che è perpendicolare a questa faccia. Condizione aggiuntiva: il volume corporeo è 60 cm 3 .
Ad
La decisione Lascia che sia nota l'area di quella faccia, che si trova di fronte all'osservatore. Se le lettere standard per le dimensioni parallelepipedo vengono prese come denominazione, alla base della costola ci saranno "a" e "b", quella verticale "c". In base a ciò, l'area di una faccia conosciuta viene definita come il prodotto "a" su "c".
Ora devi usare un volume conosciuto. La sua formula per un parallelepipedo rettangolare dà il prodotto di tutte e tre le quantità: "a", "in" e "c". Cioè, l'area conosciuta, moltiplicata per "in", dà il volume. Da qui si scopre che il bordo desiderato può essere calcolato dall'equazione:
12 * = 60.
Il calcolo elementare dà il risultato 5.
La risposta è Il bordo desiderato è di 5 cm.
Il quinto compito. Condizioni. Dato un parallelepipedo dritto. Alla sua base è un parallelogramma con lati di 6 e 8 cm, l'angolo acuto tra cui è 30º. Il bordo laterale ha una lunghezza di 5 cm. È necessario per calcolare l'area totale del parallelepipedo.
La decisione Questo è il caso in cui è necessario conoscere l'area di tutti i volti separatamente. O, più precisamente, tre coppie: la base e i due lati.
Poiché un parallelogramma si trova alla base, la sua area viene calcolata come prodotto del lato e l'altezza ad esso. Il lato è noto, ma l'altezza non lo è. Deve essere contato. Ciò richiederà un valore di angolo acuto. Forme di altezza in parallelogramma triangolo rettangolo. In essa la gamba è uguale al prodotto del seno dell'angolo acuto, che è opposto ad esso, dall'ipotenusa.
Lascia che il lato famoso del parallelogramma sia "a". Quindi l'altezza sarà scritta come * sin 30º. Pertanto, l'area di base è a * c * sin 30º.
Con i bordi laterali, tutto è più facile. Sono rettangoli. Pertanto, la loro area è il prodotto di una parte all'altra. Il primo - a * s, il secondo - in * s.
Resta da combinare tutto in un'unica formula e contare:
S = 2 * (a * b * sin 30º + a * s + b * s)
Dopo la sostituzione di tutte le quantità, risulta che l'area richiesta è 188 cm 2 .
La risposta è S = 188 cm 2 .