Scomposizione di trinomi quadrati in fattori: esempi e formule

Scomporre quadrilateri quadrati in fattori si riferisce a compiti scolastici che tutti affrontano prima o poi. Come si fa? Qual è la formula per la scomposizione dei fattori trinomiali quadrati? Capiremo passo dopo passo gli esempi.

Formula generale

La scomposizione dei trinomi quadrati in fattori viene effettuata risolvendo un'equazione quadratica. Questo è un compito semplice che può essere risolto con diversi metodi - trovando il discriminante, usando il teorema di Vieta, c'è anche una soluzione grafica. I primi due metodi sono studiati al liceo.

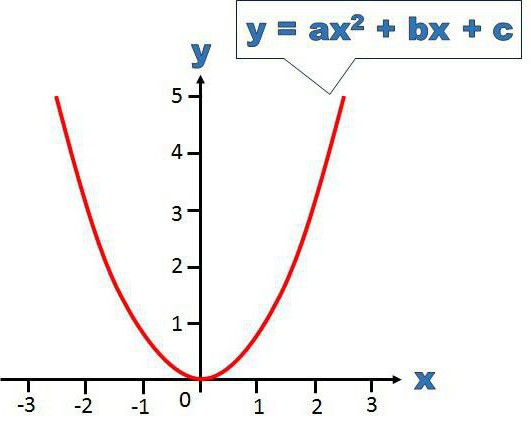
lx ² +kx+n=l(xx ₁ )(xx ₂ ) (1) La formula generale è la seguente: lx ² + kx + n = l (xx ₁ ) (xx ₂ ) (1)

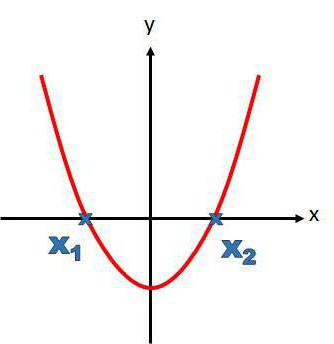
Algoritmo di esecuzione del compito

Per eseguire una fattorizzazione di trinomiali quadrati, è necessario conoscere il teorema di Vit, avere una soluzione a portata di mano, essere in grado di trovare una soluzione graficamente o cercare le radici di un'equazione di secondo grado attraverso la formula discriminante. Se viene fornito un trinomio quadrato e deve essere fattorizzato, la sequenza di azioni è la seguente:

1) Equare l'espressione originale a zero per ottenere l'equazione.

2) Porta questi termini (se c'è una tale necessità).

3) Trova le radici in qualsiasi modo conosciuto. Il metodo grafico viene utilizzato al meglio se è noto in anticipo che le radici sono numeri interi e piccoli. Va ricordato che il numero di radici è uguale al massimo grado dell'equazione, cioè, equazione quadratica due radici.

4) Sostituisci il valore di x nell'espressione (1).

5) Annotare la scomposizione dei fattori trinomiali quadrati.

esempi

Finalmente capire come questo compito viene eseguito, consente la pratica. Illustrare il factoring degli esempi trinomiali quadrati:

È necessario espandere l'espressione:

x ² -17x = -32

Ricolleghiamo al nostro algoritmo:

1) x ² -17x + 32 = 0

2) termini simili sono ridotti

3) secondo la formula Viet, è difficile trovare le radici per questo esempio, perché è meglio usare l'espressione per la discriminante:

D = 289-128 = 161 = (12,69) ²

x ₁ = 2.155

x ₂ = 14.845

4) Sostituisci le radici che abbiamo trovato nella formula di base per la decomposizione:

(x-2.155) _* (x-14.845)

5) Quindi la risposta sarà:

x ² -17x + 32 = (x-2.155) (x-14.845)

Verifica se le soluzioni trovate dal discriminante corrispondono alle formule Viet:

2.155 + 14.845 = 17

14.845 ^. 2.155 = 32

Per queste radici, viene applicato il teorema di Viet, sono stati trovati correttamente, il che significa che anche la fattorizzazione che abbiamo ottenuto è corretta.

Analogamente decompone 12x ² + 7x-6.

12x ² + 7x-6 = 0

D = 337

x ₁ = -7 + (337) ^1/2

x ₂ = -7- (337) ^1/2

Nel caso precedente, le soluzioni erano non-inte, ma numeri reali, che sono facili da trovare, avendo una calcolatrice di fronte a voi. Consideriamo ora un esempio più complesso in cui le radici saranno complesse: factoring x ² + 4x + 9. Secondo la formula di Vieta, le radici non possono essere trovate e la discriminante è negativa. Le radici saranno sul piano complesso.

D = -20

Procedendo da questo, otteniamo le radici interessanti -4 + 2i * 5 ^1/2 e -4-2i _* 5 ^1/2 , perché (-20) ^1/2 = 2i * 5 ^1/2 .

Otteniamo la decomposizione desiderata, sostituendo le radici nella formula generale.

Un altro esempio: è necessario calcolare l'espressione 23x ² -14x + 7.

=0 Abbiamo l'equazione 23x 2 -14x + 7 = 0

D = -448

Ciò significa che le radici sono 14 + 21,166i e 14-21,166i. La risposta sarà:

23x 2 -14x + 7 = 23 (x-14-21,166i) * (x-14 + 21,166i).

Facciamo un esempio, che può essere risolto senza l'aiuto di una discriminante.

Supponiamo di aver bisogno di espandere l'equazione quadratica x 2 -32x + 255. Ovviamente, può essere risolto dal discriminante, ma in questo caso è più rapido raccogliere le radici.

x 1 = 15

x 2 = 17

Quindi x 2 -32x + 255 = (x-15) (x-17).