Sequenza di Fibonacci e principi della Sezione d'oro

La sequenza di Fibonacci, che divenne nota alla maggioranza attraverso il film e il libro del Codice Da Vinci, è una serie di numeri derivati ​​dal matematico italiano Leonardo da Pisa, meglio conosciuto con lo pseudonimo di Fibonacci, nel XIII secolo. I seguaci dello scienziato hanno notato che la formula alla quale questa serie di numeri è subordinata trova il proprio riflesso nel mondo che ci circonda e risuona con altre scoperte matematiche, aprendo così la porta per noi ai segreti dell'universo. In questo articolo, descriveremo la sequenza di Fibonacci, considereremo esempi della mappatura di questo modello in natura e confrontiamolo con altre teorie matematiche.

Formulazione e definizione

La serie di Fibonacci è una sequenza matematica, ogni elemento di cui è uguale alla somma dei due precedenti. Lascia che qualche membro della sequenza sia _xn. Quindi, otteniamo una formula valida per l'intera serie: _{xn + 2} = _xn + _{xn + 1.} Con questo ordine di sequenza sarà simile a questa: 1, 1, 2, 3, 5, 8, 13, 21, 34. Il numero successivo sarà 55, poiché la somma di 21 e 34 è 55. E così via con lo stesso principio.

Esempi nell'ambiente

Se guardiamo la pianta, in particolare, sulla corona delle foglie, notiamo che fioriscono a spirale. Gli angoli si formano tra le foglie vicine, che a loro volta formano la sequenza matematica corretta di Fibonacci. Grazie a questa caratteristica, ogni singola foglia che cresce su un albero riceve la massima quantità di luce e calore.

Puzzle matematico di Fibonacci

Il famoso matematico ha presentato la sua teoria come un enigma. Suona come segue. Puoi mettere un paio di conigli in uno spazio chiuso per scoprire quante coppie di conigli nasceranno entro un anno. Data la natura di questi animali, il fatto che ogni mese una coppia è in grado di produrre una nuova coppia, e sono pronti a riprodursi dopo aver raggiunto due mesi, alla fine ha ricevuto il suo famoso numero di numeri: 1, 1, 2, 3, 5, 8 , 13, 21, 34, 55, 89, 144 - dove viene mostrato il numero di nuove coppie di conigli in ciascun mese.

Sequenza di Fibonacci e rapporto proporzionale

Questa serie ha diverse sfumature matematiche che devi assolutamente considerare. Lui, avvicinandosi più lentamente e più lentamente (asintoticamente), tende a un rapporto proporzionale. Ma è irrazionale. In altre parole, è un numero con una sequenza imprevedibile e infinita di numeri decimali nella parte frazionaria. Ad esempio, il rapporto tra qualsiasi elemento della serie varia attorno al numero 1.618, quindi supera, quindi raggiungendolo. Quanto segue per analogia si avvicina a 0.618. Ciò che è inversamente proporzionale al numero 1.618. Se dividiamo gli elementi attraverso uno, otteniamo 2.618 e 0.382. Come hai già capito, sono anche inversamente proporzionali. I numeri risultanti sono chiamati coefficienti di Fibonacci. E ora spiegheremo perché abbiamo eseguito questi calcoli.

Golden ratio

Distinguiamo tutti gli oggetti intorno a noi secondo determinati criteri. Uno di questi è la forma. Alcuni di noi attraggono di più, altri meno e altri non li gradiscono. Si nota che un oggetto simmetrico e proporzionale è molto più facile percepito dall'uomo e provoca una sensazione di armonia e bellezza. L'intera immagine include sempre parti di dimensioni diverse che si trovano in un certo rapporto tra loro. Da qui la risposta alla domanda su quella che viene chiamata la Sezione d'oro. Questo concetto significa la perfezione della relazione tra il tutto e le parti in natura, scienza, arte e ecc. Da un punto di vista matematico, considera il seguente esempio. Prendi un segmento di qualsiasi lunghezza e dividilo in due parti in modo che la parte più piccola si riferisca a quella più grande come la somma (la lunghezza dell'intero segmento) a quella più grande. Quindi, prendiamo il segmento c per il valore di uno. La sua parte sarà pari a 0,618, la seconda parte b , risulta essere uguale a 0,382. Pertanto, siamo conformi alla condizione della Sezione aurea. Il rapporto tra il segmento c e un uguale a 1,618. E il rapporto tra le parti c e b è 2.618. Otteniamo i coefficienti di Fibonacci già noti a noi. Con lo stesso principio, vengono costruiti un triangolo d'oro, un rettangolo d'oro e un cubo d'oro. Vale anche la pena notare che il rapporto proporzionale tra le parti del corpo umano è vicino alla sezione aurea.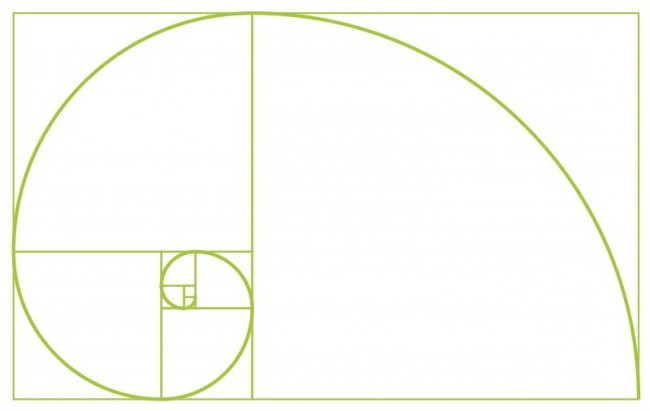

La sequenza di Fibonacci è la base di tutto?

Proviamo a combinare la teoria della Sezione d'oro e la famosa serie di matematici italiani. Iniziamo con due quadrati della prima dimensione. Quindi in cima aggiungiamo un altro quadrato della seconda dimensione. Disegniamo accanto alla stessa figura con la lunghezza del lato uguale alla somma dei due lati precedenti. Allo stesso modo disegna un quadrato della quinta dimensione. E così puoi continuare all'infinito finché non ti annoierai. La cosa principale è che la dimensione del lato di ogni quadrato successivo è uguale alla somma dei valori dei lati dei due precedenti. Otteniamo una serie di poligoni la cui lunghezza è Numeri di Fibonacci Queste figure sono chiamate rettangoli di Fibonacci. Disegniamo una linea liscia attraverso gli angoli dei nostri poligoni e otteniamo ... una spirale di Archimede! Aumentare il tono di questa figura, come sai, è sempre uniforme. Se accendi la fantasia, l'immagine risultante può essere associata alla conchiglia. Da ciò possiamo concludere che la sequenza di Fibonacci è la base di rapporti proporzionali e armoniosi di elementi nel mondo circostante.

Sequenza matematica e universo

Se guardi da vicino, la spirale di Archimede (da qualche parte esplicitamente, ma da qualche parte velata) e, quindi, il principio di Fibonacci può essere rintracciato in molti dei soliti elementi naturali che circondano una persona. Ad esempio, lo stesso guscio di vongole, i fiori di broccoli, il fiore di girasole, il cono conifere e simili. Se guardiamo da un'altra parte, vedremo la sequenza di Fibonacci in infinite galassie. Anche una persona, essendo ispirata dalla natura e adottando la sua forma, crea oggetti in cui la serie di cui sopra può essere rintracciata. Ora è il momento di richiamare la sezione aurea. Insieme al modello di Fibonacci, i principi di questa teoria sono tracciati. Esiste una versione che la sequenza di Fibonacci è una sorta di test della natura per adattarsi a una sequenza logaritmica più perfetta e fondamentale della Sezione aurea, che è quasi identica, ma non ha inizio ed è infinita. La natura della natura è tale che deve avere il suo punto di partenza, da cui partire per creare qualcosa di nuovo. La relazione dei primi elementi della serie di Fibonacci è lontana dai principi della Sezione aurea. Tuttavia, più continuiamo a farlo, più questa discrepanza viene attenuata. Per determinare la sequenza, è necessario conoscere i suoi tre elementi che si susseguono. Per la sequenza d'oro, ne bastano due. Dal momento che è sia aritmetico che progressione geometrica.

conclusione

Tuttavia, basandomi su quanto sopra, puoi porre domande abbastanza logiche: "Da dove venivano questi numeri? Chi è l'autore di tutto il mondo che ha cercato di renderlo perfetto? Era tutto sempre come voleva? Se sì, perché è fallito?" Cosa succederà dopo? " Trovando la risposta a una domanda, ottieni quella successiva. L'ho risolto - ne compaiono altri due. Dopo averli risolti, ne prendi altri tre. Dopo averli affrontati, riceverai cinque domande irrisolte. Poi otto, poi tredici, ventuno, trentaquattro, cinquantacinque ...