Accelerazione completa e componenti. Accelerazione tangenziale e accelerazione normale. Formule e esempi di soluzione dei problemi
Nella cinematica, è necessario conoscere la sua velocità e accelerazione al fine di determinare in modo univoco le caratteristiche del movimento del corpo in qualsiasi punto della traiettoria. La dipendenza temporale di queste quantità fornisce tutte le informazioni necessarie per calcolare il percorso percorso dal corpo. Consideriamo più in dettaglio nell'articolo cos'è l'accelerazione tangenziale e l'accelerazione normale.
In fisica
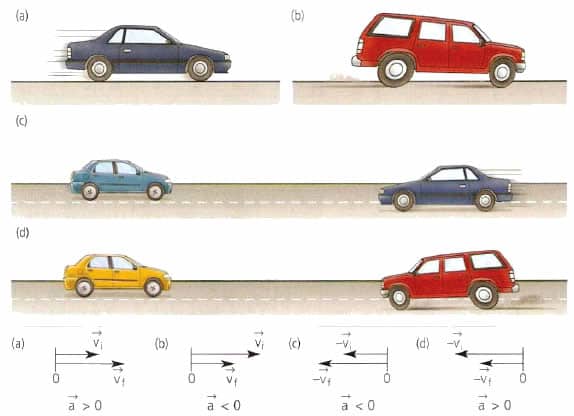
Prima di considerare l'accelerazione per il movimento meccanico, l'accelerazione normale e tangenziale, facciamo la conoscenza del concetto fisico stesso. La definizione di accelerazione è abbastanza semplice. In fisica, sotto esso capisce il cambiamento caratteristico della velocità. Quest'ultima è una quantità vettoriale che determina la velocità di cambiamento delle coordinate di un oggetto in movimento nello spazio. La velocità è misurata in metri al secondo (distanza percorsa per unità di tempo). Se è indicato dal simbolo v¯, allora la definizione matematica dell'accelerazione a sarà simile a questa:
a¯ = dv¯ / dt
Questa uguaglianza definisce la cosiddetta accelerazione istantanea completa. Si chiama istantaneo perché caratterizza il cambio di velocità solo in un dato momento.
Se il movimento è ugualmente accelerato, cioè per lungo tempo, l'accelerazione non cambia il suo modulo e la sua direzione, quindi possiamo scrivere la seguente formula per determinarla:
a¯ = Δv¯ / Δt
Dove Δt >> dt. Il valore di a qui è chiamato l'accelerazione media, che è generalmente diversa dall'istante.
L'accelerazione viene misurata nel sistema SI in metri al secondo quadrato (m / s 2 ).
Traiettoria e componenti di piena accelerazione
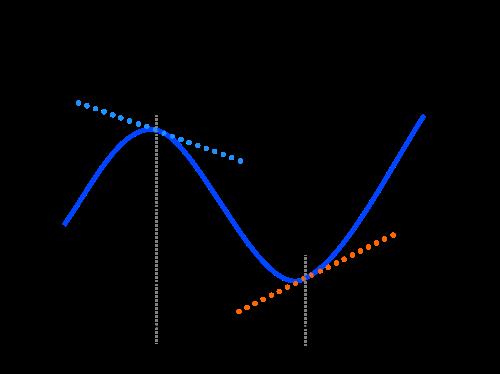
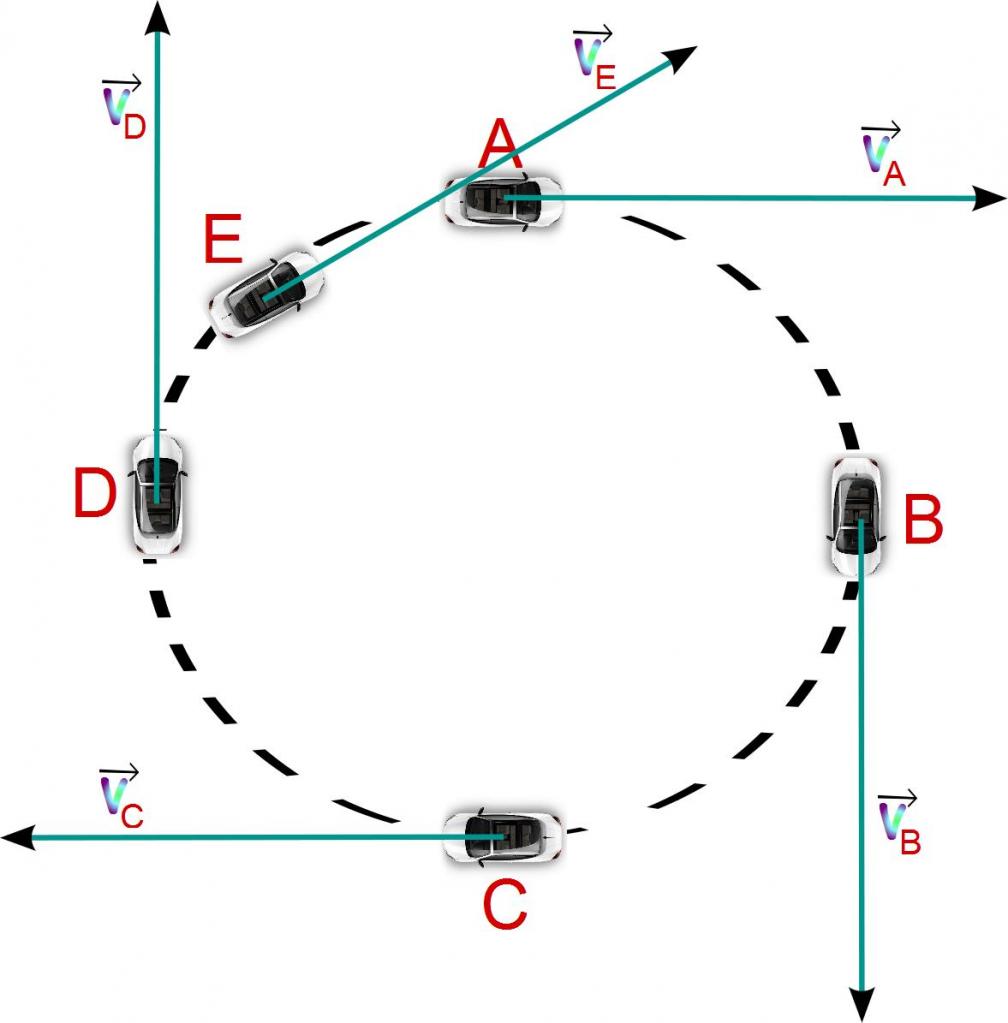
Molto spesso, i corpi in natura si muovono lungo traiettorie curve. Esempi di un tale movimento sono: rotazione dei pianeti nelle loro orbite, caduta parabolica di una pietra sulla terra, rotazione delle auto. Nel caso di una traiettoria curvilinea in qualsiasi momento, la velocità viene diretta tangenzialmente al punto di traiettoria in questione. Come viene diretta l'accelerazione?
Per rispondere alla domanda di cui sopra, scriviamo la velocità del corpo nella seguente forma:
v¯ = v * u t ¯
Qui, u t ¯ è il vettore di velocità unitaria, il pedice t significa che è diretto tangenzialmente alla traiettoria (componente tangenziale). Il simbolo v indica il modulo di velocità v.
Ora, seguendo la definizione di accelerazione, possiamo differenziare la velocità rispetto al tempo, abbiamo:
a¯ = dv¯ / dt = dv / dt * u t ¯ + v * d (u t ¯) / dt
Quindi, l'accelerazione totale a ¯ è la somma vettoriale di due componenti. Il primo e il secondo termine sono chiamati accelerazione normale e tangenziale del punto. Dai uno sguardo più da vicino a ciascuno di questi componenti.
Ad
Accelerazione tangenziale
Scriviamo ancora una volta la formula per questo componente di piena accelerazione:
un t ¯ = dv / dt * u t ¯
Questa espressione ci permette di descrivere le proprietà di un t ¯:
- È diretto allo stesso modo della velocità stessa o opposta ad esso, cioè lungo la tangente alla traiettoria. Ciò è evidenziato dal vettore elementare u t ¯.
- Caratterizza il cambio di velocità in valore assoluto, che si riflette sul fattore dv / dt.
Queste proprietà ci permettono di trarre una conclusione importante: per il moto rettilineo, le accelerazioni complete e tangenziali hanno lo stesso valore. Nel caso di un movimento curvo, l'accelerazione totale è sempre maggiore di quella tangenziale. Quando si considerano compiti fisici per moto rettilineo uniformemente accelerato, stanno parlando di questo componente dell'accelerazione.
Accelerazione normale
Considerando il tema della velocità, dell'accelerazione della tangenziale e dell'accelerazione della normale, diamo una descrizione dell'ultimo valore. Scriviamo la formula per questo:
a n ¯ = v * d (u t ¯) / dt = v * d (u t ¯) / dL * dL / dt
Per scrivere esplicitamente il lato destro dell'uguaglianza, usiamo le seguenti relazioni:
dL / dt = v;
d (u t ¯) / dL = 1 / r
Qui dL è la distanza percorsa dal corpo nell'intervallo di tempo dt, r è il raggio di curvatura della traiettoria. La prima espressione corrisponde alla definizione di velocità, la seconda uguaglianza segue da considerazioni geometriche. Usando queste formule, otteniamo l'espressione finale per l'accelerazione normale:
Ad
a n ¯ = v 2 / r
Cioè, il valore di un n ¯ non dipende dal cambiamento di velocità, come componente tangenziale, ma è determinato unicamente dal suo modulo. L'accelerazione normale lungo la normale a questa parte della traiettoria è diretta, cioè verso il centro di curvatura. Ad esempio, mentre si muove lungo un cerchio, il vettore a n è diretto al suo centro, quindi, l'accelerazione normale è spesso chiamata centripeta.
Se l'accelerazione è tangenziale per il cambiamento nell'ampiezza della velocità, allora la componente normale è responsabile del cambiamento nel vettore di velocità, cioè determina la traiettoria del corpo.
Accelerazione completa, normale e tangenziale
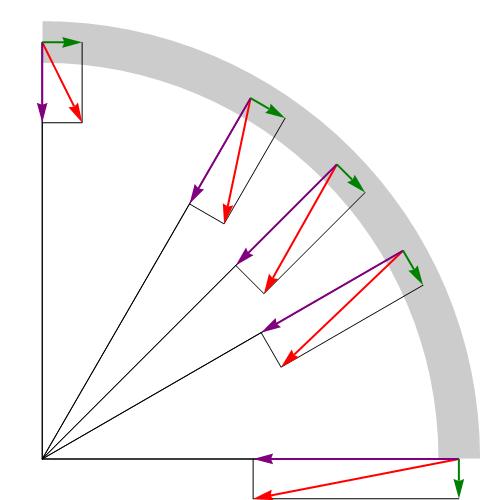
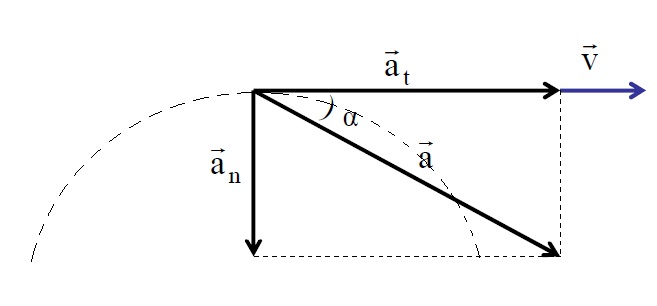
Avendo affrontato il concetto di accelerazione e le sue componenti, ora diamo una formula che ci consente di determinare l'accelerazione completa. Poiché i componenti considerati sono diretti ad un angolo di 90 ° l' uno dall'altro, il teorema di Pitagora può essere usato per determinare il valore assoluto della loro somma vettoriale. La formula per l'accelerazione completa è:
a = √ (a t 2 + a n 2 )
La direzione della grandezza di a può essere determinata rispetto al vettore di uno qualsiasi dei componenti. Ad esempio, l'angolo tra a¯ e a ¯ è calcolato come:
θ = arctan (a t / a n )
Tenendo conto della formula precedente per il modulo a, possiamo concludere: con moto uniforme lungo un cerchio, l'accelerazione completa coincide con quella centripeta.
Problem solving
Lascia che il corpo si muova in un cerchio con un raggio di 1 metro. È noto che la sua velocità varia in base alla seguente legge:
v = 2 * t 2 + 3 * t
È necessario determinare l'accelerazione tangenziale e l'accelerazione normale al momento t = 4 secondi.
Per tangenziale abbiamo:
a t = dv / dt = 4 * t + 3 = 19 m / s 2
Per trovare il modulo di accelerazione normale, è necessario innanzitutto calcolare il valore di velocità in un dato punto nel tempo. Abbiamo:
v = 2 * 4 2 + 3 * 4 = 44 m / s
Ora puoi usare la formula per un n :
a n = v 2 / r = 44 2/1 = 1936 m / s 2
Quindi, abbiamo determinato tutte le quantità necessarie per trovare il problema.