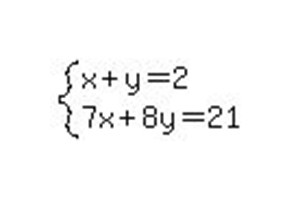Metodo di Gauss per la risoluzione di matrici. Soluzione di un sistema di equazioni lineari con il metodo di Gauss

Dall'inizio del XVI-XVIII secolo, i matematici hanno iniziato a studiare intensamente le funzioni a causa delle quali tanto è cambiato nella nostra vita. La tecnologia informatica senza questa conoscenza semplicemente non esisterebbe. Per risolvere problemi complessi, equazioni lineari e funzioni, sono stati creati vari concetti, teoremi e metodi di soluzione. Uno di questi metodi e metodi universali e razionali per risolvere equazioni lineari e i loro sistemi era il metodo di Gauss. Matrici, il loro grado, determinante: tutto può essere calcolato senza utilizzare operazioni complesse.

Cos'è un slau

In matematica, c'è il concetto di SLAE - un sistema di equazioni algebriche lineari. Com'è lei? Questo è un insieme di equazioni m con le variabili sconosciute n sconosciute, solitamente denotate come x, y, z, o x ₁ , x ₂ ... x _n, o altri simboli. Risolvere questo sistema usando il metodo di Gauss significa trovare tutte le incognite sconosciute. Se il sistema ha lo stesso numero di incognite ed equazioni, allora viene chiamato un sistema di ordine n.

I metodi più popolari per risolvere slaf

Nelle istituzioni educative di istruzione secondaria studiano vari metodi per risolvere tali sistemi. Molto spesso si tratta di semplici equazioni composte da due incognite, quindi qualsiasi metodo esistente per trovare la risposta non richiederà molto tempo. Questo può essere un metodo di sostituzione, quando un altro è derivato da un'equazione e sostituito in quello originale. O il metodo del termine per sottrazione e addizione. Ma il metodo di Gauss è considerato il più semplice e universale. Rende possibile risolvere equazioni con qualsiasi numero di incognite. Perché questa tecnica è considerata razionale? È semplice Il metodo matrix è buono perché non è necessario riscrivere i caratteri non necessari più volte come sconosciuto, è sufficiente fare operazioni aritmetiche sui coefficienti e ottenere un risultato affidabile.

Dove vengono utilizzati gli SLAE nella pratica

La soluzione di SLAE è i punti di intersezione delle linee sui grafici delle funzioni. Nella nostra era dei computer high-tech, le persone che sono strettamente connesse con lo sviluppo di giochi e altri programmi devono sapere come risolvere tali sistemi, cosa rappresentano e come verificare la correttezza del risultato ottenuto. Molto spesso, i programmatori sviluppano programmi per computer speciali per l'algebra lineare, e questo include un sistema di equazioni lineari. Il metodo Gauss consente di calcolare tutte le soluzioni esistenti. Vengono anche utilizzate altre formule e tecniche semplificate.

Criterio di compatibilità SLAU

Un tale sistema può essere risolto solo se è compatibile. Per chiarezza, rappresentiamo lo SLAE come Ax = b. Ha una soluzione se rang (A) è uguale a rang (A, b). In questo caso (A, b) è una matrice di tipo esteso, che può essere ottenuta dalla matrice A riscrivendola con membri liberi. Risulta che risolva equazioni lineari Il metodo di Gauss è abbastanza semplice.

Forse qualche notazione non è completamente chiara, quindi è necessario guardare a tutto con un esempio. Supponiamo che esista un sistema: x + y = 1; 2x-3y = 6. Consiste di solo due equazioni, in cui 2 sono sconosciute. Il sistema avrà una soluzione solo se il rango della sua matrice è uguale al rango della matrice espansa. Qual è il grado? Questo è il numero di linee indipendenti del sistema. Nel nostro caso, il rango della matrice è 2. La matrice A consisterà dei coefficienti situati vicino alle incognite, ei coefficienti dietro il segno "=" si adattano anche alla matrice estesa.

Perché SLAE può essere rappresentato in forma matriciale

Sulla base del criterio di compatibilità secondo il comprovato teorema di Kronecker-Capelli, il sistema di equazioni algebriche lineari può essere rappresentato in una matrice. Utilizzando il metodo a cascata Gauss, è possibile risolvere la matrice e ottenere l'unica risposta affidabile all'intero sistema. Se il grado di una matrice ordinaria è uguale al grado della matrice espansa, ma è inferiore al numero di incognite, il sistema ha un numero infinito di risposte.

Trasformazioni di matrici

Prima di procedere alla soluzione delle matrici, è necessario sapere quali azioni possono essere eseguite sui loro elementi. Ci sono diverse trasformazioni elementari:

• Riscrivendo il sistema in una vista a matrice e implementando la sua soluzione, è possibile moltiplicare tutti gli elementi di una riga per lo stesso coefficiente.
• Per convertire la matrice in una forma canonica, è possibile scambiare due righe parallele. La forma canonica implica che tutti gli elementi della matrice, che si trovano sulla diagonale principale, diventano unità, e i rimanenti - zeri.
• Gli elementi corrispondenti delle righe parallele della matrice possono essere aggiunti l'uno all'altro.

Metodo Jordan-Gauss

L'essenza di risolvere sistemi di equazioni lineari omogenee e non omogenee con il metodo di Gauss è eliminare gradualmente le incognite. Supponiamo di avere un sistema di due equazioni in cui ci sono due incognite. Per trovarli, è necessario verificare la compatibilità del sistema. L'equazione con il metodo di Gauss è risolta in modo molto semplice. È necessario scrivere i coefficienti situati vicino a ogni sconosciuto nella vista matrice. Per risolvere il sistema, dovrai scrivere la matrice estesa. Se una delle equazioni contiene un numero minore di incognite, è necessario inserire "0" al posto dell'elemento mancante. Tutti i metodi di trasformazione noti sono applicati alla matrice: moltiplicazione, divisione per numero, aggiunta degli elementi corrispondenti delle righe tra loro e altri. Si scopre che in ogni riga è necessario lasciare una variabile con il valore "1", il resto porta alla forma zero. Per una comprensione più accurata, è necessario considerare il metodo di Gauss con esempi.

Un semplice esempio di una soluzione di sistema 2x2.

Per prima cosa prendiamo un semplice sistema di equazioni algebriche in cui ci saranno 2 incognite.

Riscrivilo in una matrice espansa.

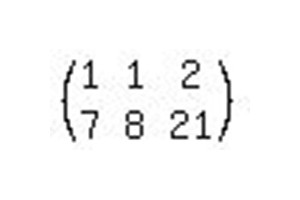
Per risolvere questo sistema di equazioni lineari, è necessario eseguire solo due operazioni. Abbiamo bisogno di portare la matrice alla forma canonica in modo che le unità stiano lungo la diagonale principale. Quindi, trasferendo dalla vista matrice al sistema, otteniamo le equazioni: 1x + 0y = b1 e 0x + 1y = b2, dove b1 e b2 sono le risposte risultanti nel processo di soluzione.

1. Il primo passo per risolvere la matrice espansa sarebbe: la prima riga deve essere moltiplicata per -7 e gli elementi corrispondenti aggiunti alla seconda riga, rispettivamente, al fine di eliminare uno sconosciuto nella seconda equazione.
2. Poiché la soluzione delle equazioni mediante il metodo di Gauss implica la riduzione della matrice alla forma canonica, allora è necessario fare le stesse operazioni con la prima equazione e rimuovere la seconda variabile. Per fare ciò, sottraiamo la seconda riga dal primo e otteniamo la risposta necessaria: la soluzione SLAU. Oppure, come mostrato nella figura, la seconda riga viene moltiplicata per il coefficiente -1 e gli elementi della seconda riga vengono aggiunti alla prima riga. Questa è la stessa cosa

Come puoi vedere, il nostro sistema è risolto con il metodo Jordan-Gauss. Lo riscriviamo nella forma richiesta: x = -5, y = 7.

Un esempio di una soluzione SLAE 3x3

Supponiamo di avere un sistema più complesso di equazioni lineari. Il metodo Gauss rende possibile calcolare la risposta anche per il sistema apparentemente confuso stesso. Pertanto, per ottenere una visione più approfondita del metodo di calcolo, è possibile passare a un esempio più complesso con tre incognite.

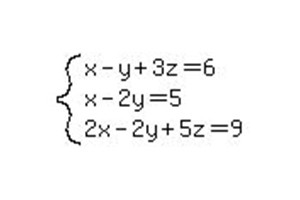
Come nell'esempio precedente, riscriviamo il sistema sotto forma di una matrice espansa e iniziamo a ridurlo a una forma canonica.

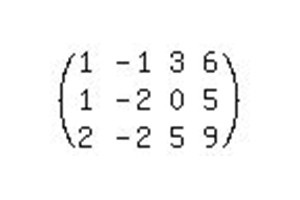
Per risolvere questo sistema, dovrai fare molti più passaggi rispetto all'esempio precedente.

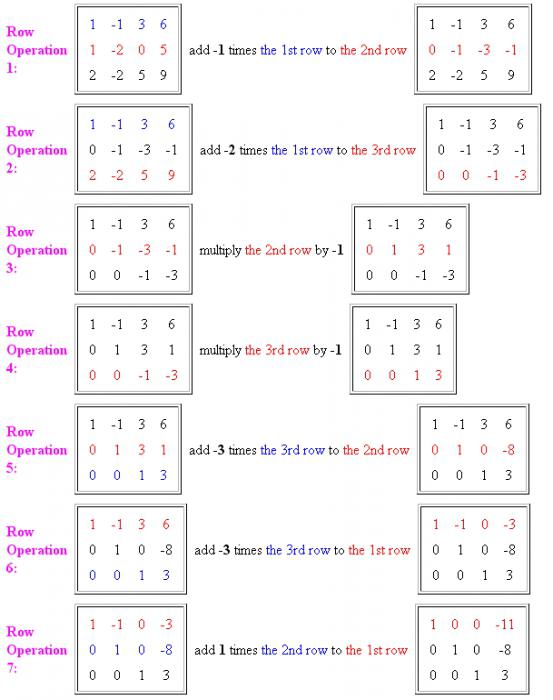
1. Per prima cosa devi fare nella prima colonna un elemento unitario e gli zeri rimanenti. Per fare ciò, moltiplica la prima equazione per -1 e aggiungi la seconda equazione ad essa. È importante ricordare che riscriviamo la prima riga nella sua forma originale e la seconda in quella modificata.
2. Quindi, rimuovere lo stesso primo sconosciuto dalla terza equazione. Per fare ciò, gli elementi della prima riga vengono moltiplicati per -2 e li aggiungono alla terza riga. Ora la prima e la seconda riga vengono riscritte nella forma originale e la terza - già con le modifiche. Come si può vedere dal risultato, abbiamo ottenuto la prima unità all'inizio della diagonale principale della matrice e gli zeri rimanenti. Altre azioni e il sistema di equazioni che usa il metodo di Gauss saranno risolti in modo affidabile.
3. Ora è necessario eseguire operazioni su altri elementi delle righe. La terza e la quarta azione possono essere combinate in una sola. È necessario dividere la seconda e la terza riga di -1 per eliminare le unità negative in diagonale. La terza linea ci ha già portato alla forma necessaria.
4. Quindi portiamo la seconda linea alla forma canonica. Per fare ciò, moltiplichiamo gli elementi della terza riga di -3 e li aggiungiamo alla seconda riga della matrice. Il risultato mostra che anche la seconda riga viene ridotta alla forma di cui abbiamo bisogno. Resta da fare qualche altra operazione e rimuovere i coefficienti delle incognite dalla prima riga.
5. Per rendere 0 dal secondo elemento della linea, è necessario moltiplicare la terza riga di -3 e aggiungerla alla prima riga.
6. Il prossimo passo cruciale aggiungerà alla prima linea gli elementi necessari della seconda fila. Quindi otteniamo la forma canonica della matrice e, di conseguenza, la risposta.

Come puoi vedere, la soluzione delle equazioni con il metodo di Gauss è abbastanza semplice.

Un esempio di soluzione di un sistema di equazioni 4x4

Alcuni sistemi di equazioni più complessi possono essere risolti con il metodo di Gauss mediante programmi per computer. È necessario guidare nelle celle vuote esistenti i coefficienti con incognite, e il programma stesso calcolerà passo per passo il risultato necessario, descrivendo ogni azione in dettaglio.

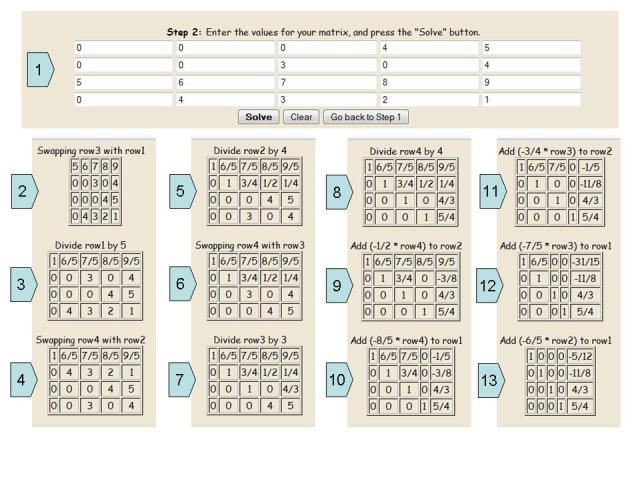
Di seguito è riportata un'istruzione passo passo per risolvere un simile esempio.

• Nella prima fase, coefficienti e numeri liberi con valori sconosciuti si adattano a celle vuote. Così, si scopre la stessa matrice estesa, che scriviamo a mano.

• Successivamente, tutte le linee sono invertite in modo che gli elementi dell'unità possano essere espressi lungo la diagonale principale.

• E vengono eseguite tutte le operazioni aritmetiche necessarie per portare la matrice espansa a una forma canonica. Dovrebbe essere compreso che la risposta al sistema di equazioni non è sempre la stessa: sono numeri interi. A volte la soluzione può essere da numeri frazionari.

Soluzione di convalida

Il metodo Jordan-Gauss prevede la verifica della correttezza del risultato. Per scoprire se i coefficienti sono calcolati correttamente, è necessario solo sostituire il risultato nel sistema originale di equazioni. Il lato sinistro dell'equazione deve corrispondere al lato destro, che è dietro il segno di uguale. Se le risposte non corrispondono, è necessario ricalcolare il sistema o provare ad applicare ad esso un altro metodo per risolvere lo SLAE a te noto, come la sostituzione o la sottrazione e l'aggiunta a termine. Dopo tutto, la matematica è una scienza che ha un enorme numero di diverse tecniche di soluzione. Ma ricorda: il risultato deve essere sempre lo stesso, indipendentemente dal metodo di soluzione che hai usato.

Metodo Gauss: gli errori più comuni durante la risoluzione di SLAE

Quando risolvono sistemi lineari di equazioni, si verificano errori come il trasferimento errato di coefficienti nella forma della matrice. Esistono sistemi in cui alcune incognite sono assenti in una delle equazioni, quindi, trasferendo i dati nella matrice espansa, possono essere persi. Di conseguenza, quando si risolve questo sistema, il risultato potrebbe non corrispondere a quello reale.

Un altro degli errori principali potrebbe essere la scrittura errata del risultato finale. È necessario comprendere chiaramente che il primo coefficiente corrisponderà al primo sconosciuto dal sistema, il secondo al secondo e così via.

Il metodo di Gauss descrive in dettaglio la soluzione delle equazioni lineari. Grazie a lui, è facile eseguire le operazioni necessarie e trovare il risultato giusto. Inoltre, è uno strumento universale per trovare una risposta affidabile alle equazioni di qualsiasi complessità. Forse è per questo che viene così spesso utilizzato per risolvere SLAE.