Come viene formulato e provato il teorema del coseno?
Non tutti gli scolari, e ancor più gli adulti, sanno che il teorema del coseno è direttamente correlato al teorema di Pitagora. Più precisamente, quest'ultimo è un caso speciale del primo. Questo momento, oltre a due modi per dimostrare il teorema del coseno, ti aiuterà a diventare una persona più competente. Inoltre, la pratica di esprimere valori dalle espressioni originali è un pensiero logico ben sviluppato. La lunga formula del teorema in esame costringerà sicuramente uno a lavorare e migliorare.
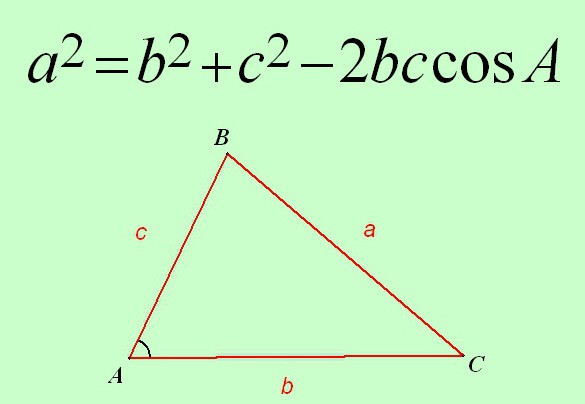
L'inizio della conversazione: l'introduzione dei simboli
Questo teorema è formulato e provato per un triangolo arbitrario. Pertanto, può sempre essere usato, in qualsiasi situazione, se vengono dati due lati, e in alcuni casi tre, e un angolo, e non necessariamente tra di loro. qualunque tipo di triangolo il teorema funziona sempre.
Ad
E ora sulla designazione delle quantità in tutte le espressioni. È meglio essere d'accordo subito, in modo da non spiegarlo più volte. Per questo, la seguente tabella è compilata.
| Elemento triangolare | La sua designazione |
| Lato sconosciuto | e |
| Altri due lati | in, con |
| Angolo opposto lato sconosciuto | la |
| Angoli che si trovano contro altri lati | B, C |
| L'altezza della parte superiore del triangolo | n |
Formulazione e scrittura matematica
Quindi, il teorema del coseno è formulato come segue:
Il quadrato del lato di qualsiasi triangolo è uguale alla somma dei quadrati degli altri due lati di esso, meno il doppio del prodotto degli stessi lati dal coseno dell'angolo che si trova tra di loro.
Certo, è lungo, ma se capisci la sua essenza, allora sarà facile da ricordare. Puoi anche immaginare un disegno di un triangolo. Visivamente sempre più facile da ricordare.
La formula di questo teorema sarà simile a questa:
a 2 = 2 + s 2 - 2 * c * s * cos A.
Un po 'lungo, ma tutto è logico. Se guardi un po 'più da vicino, puoi vedere che le lettere sono ripetute, quindi è facile da ricordare.
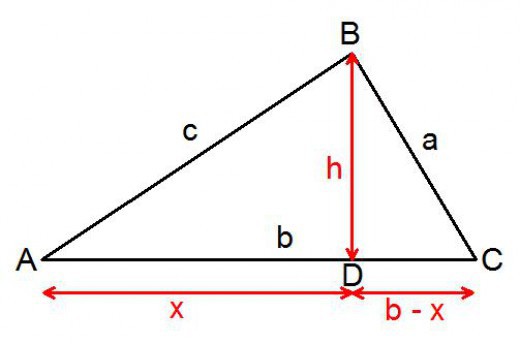
Prova comune del teorema
Poiché è valido per tutti i triangoli, è possibile scegliere per il ragionamento di uno qualsiasi dei tipi. Lascia che sia una figura con tutti gli angoli acuti. Considera un triangolo acuto arbitrario il cui angolo C è maggiore dell'angolo B. Dal vertice con questo angolo grande, devi abbassare la perpendicolare al lato opposto. L'altezza contenuta divide il triangolo in due rettangolari. Questo è richiesto per la prova.
Ad
Il lato sarà diviso in due segmenti: x, y. Devono essere espressi in termini noti. La parte che risulta essere in un triangolo con un'ipotenusa uguale a, sarà espressa scrivendo:
x = in * cos A.
L'altro sarà uguale a questa differenza:
y = s - in * cos A.
Ora abbiamo bisogno di scrivere il teorema di Pitagora per i due risultati triangoli rettangoli prendendo un'altezza sconosciuta. Queste formule avranno questo aspetto:
n 2 = in 2 - (in * cos А) 2 ,
n 2 = a 2 - (c - c * cos A) 2 .
In queste uguaglianze sono identiche espressioni a sinistra. Quindi, anche i loro lati positivi saranno uguali. È facile da scrivere Ora è necessario aprire le parentesi:
in 2 - in 2 * (cos À) 2 = a 2 - ñ 2 + 2 с * in * cos А - in 2 * (cos À) 2 .
Se eseguiamo il trasferimento e la riduzione di tali termini, allora otteniamo la formula iniziale, che è scritta dopo la dicitura, cioè il teorema del coseno. La dimostrazione è completa.
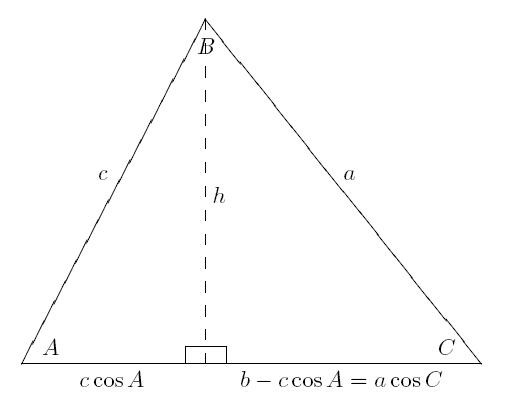
Prova del teorema attraverso i vettori
È molto più corto di quello precedente. E se conosci le proprietà dei vettori, allora il teorema del coseno per il triangolo sarà dimostrato semplicemente.
Se i lati a, b, c sono indicati rispettivamente dai vettori BC, AC e AB, allora l'uguaglianza è vera:
SU = AC - AB.
Ora devi eseguire alcune azioni. Il primo di questi è la quadratura di entrambi i lati dell'uguaglianza:
BC 2 = AC 2 + AB 2 - 2 AC * AB.
Quindi l'uguaglianza deve essere riscritta in forma scalare, dato che il prodotto dei vettori è uguale al coseno dell'angolo tra loro e i loro valori scalari:
BC 2 = AC 2 + AB 2 - 2 AC * AB * cos A.
Resta solo da ritornare alla vecchia notazione, e di nuovo il teorema del coseno si rivelerà:
a 2 = 2 + s 2 - 2 * c * s * cos A.
Formule per altri lati e tutti gli angoli
Per trovare il lato, dal teorema del coseno è necessario estrarre radice quadrata. La formula per i quadrati di uno degli altri lati sarà simile a questa:
con 2 = a 2 + a 2 - 2 * a * a * cos C.
Per scrivere l'espressione per il quadrato del lato in , è necessario sostituire l'uguaglianza precedente con da a, e viceversa, e posizionare l'angolo B sotto il coseno
Dalla formula di base del teorema, possiamo esprimere il valore del coseno dell'angolo A:
cos А = (in 2 + с 2 - а 2 ) / (2 в * с).
Le formule per altri angoli sono derivate allo stesso modo. Questa è una buona pratica, quindi puoi provare a scriverli da solo.
Naturalmente, non è necessario memorizzare queste formule. Basta capire il teorema e la capacità di derivare queste espressioni dalla sua registrazione principale.
La formula originale del teorema consente di trovare un lato se l'angolo non è tra i due noti. Ad esempio, è necessario trovare in , quando vengono forniti i valori: a, c, a . O è sconosciuto con , ma ci sono valori a, b, a .
Ad
In questa situazione, è necessario spostare tutte le formule di aggiunta a sinistra. Questa uguaglianza è ottenuta:
ñ 2 - 2 * в * с * cos А + в 2 - а 2 = 0.
Riscrivialo in una forma leggermente diversa:
con 2 - (2 * in * cos A) * con + (in 2 - e 2 ) = 0.
Puoi facilmente vedere l'equazione quadratica. In esso, la quantità sconosciuta è c , e tutti gli altri sono dati. Pertanto, è sufficiente risolverlo con l'aiuto di una discriminante. Quindi verrà trovato il lato sconosciuto.
Allo stesso modo, si ottiene la formula per il secondo lato:
2 - (2 * s * cos A) * c + (c 2 - a 2 ) = 0.
Da altre espressioni, tali formule sono anche facili da ottenere.
Come calcolare l'angolo senza calcolare il coseno?
Se osservate attentamente la formula dell'angolo del coseno derivata in precedenza, noterete quanto segue:
- il denominatore di una frazione è sempre un numero positivo, perché contiene il prodotto di lati che non possono essere negativi;
- l'angolo dipenderà dal segno del numeratore.
L'angolo A sarà:
- acuta in una situazione in cui il numeratore è maggiore di zero;
- smussato se questa espressione è negativa;
- diretto quando è zero.
A proposito, quest'ultima situazione trasforma il teorema del coseno nel teorema di Pitagora. Perché con un angolo di 90 °, il suo coseno è zero e l'ultimo termine scompare.
Primo compito
condizione
L'angolo ottuso di un triangolo arbitrario è 120º. A proposito dei lati a cui è limitato, è noto che uno di essi è più lungo di 8 cm rispetto all'altro: la lunghezza del terzo lato è nota, è di 28 cm. È necessario trovare il perimetro del triangolo.
Ad
decisione
Per prima cosa è necessario designare uno dei lati con la lettera "x". In questo caso, l'altro sarà uguale a (x + 8). Dato che ci sono espressioni per tutti e tre i lati, puoi usare la formula che il teorema del coseno dà:
28 2 = (x + 8) 2 + x 2 - 2 * (x + 8) * x * cos 120º.
Nelle tabelle per i coseni, è necessario trovare un valore corrispondente a 120 gradi. Questo sarà il numero 0.5 con un segno meno. Ora è necessario aprire le parentesi, osservare tutte le regole e dare termini simili:
784 = x 2 + 16x + 64 + x 2 - 2x * (-0,5) * (x + 8);
784 = 2x 2 + 16x + 64 + x 2 + 8x;
3x 2 + 24x - 720 = 0.
Questa equazione quadratica viene risolta trovando il discriminante, che sarà uguale a:
D = 24 2 - 4 * 3 * (- 720) = 9216.
Poiché il suo valore è maggiore di zero, l'equazione ha due risposte radice.
x 1 = ((-24) + √ (9216)) / (2 * 3) = 12;
x 2 = ((-24) - √ (9216)) / (2 * 3) = -20.
L'ultima radice non può essere la risposta del problema, perché la parte deve essere necessariamente positiva.
Quindi i due lati sono noti. Facile da trovare il terzo: 12 + 8 = 20 (cm). Ora puoi rispondere alla domanda del problema. Perimetro di un triangolo è definita come la somma di tutte le parti:
24 + 12 + 20 = 60 (cm).
Risposta : il perimetro è di 60 centimetri.

Problema numero 2
condizione
Nel triangolo sono noti: c , pari a 2 cm; a , che è di 10 cm; angolo C di 120º. Necessario per trovare una parte in
decisione
Per prima cosa è necessario utilizzare il teorema del coseno e derivare la formula equazione quadratica in cui il valore in sarà sconosciuto:
con 2 = a 2 + in 2 - 2 * a * in * cos C
e
in 2 - (2 * a * cos C) * in + (a 2 - c 2 ) = 0.
È necessario sostituire tutti i valori noti nella condizione:
in 2 - (2 * 10 * cos 120º) * in + (10 2 - 2 2 ) = 0.
Ora dobbiamo contare ciò che è possibile per semplificare l'espressione:
in 2 - (20 * (-1/2)) * in + (100 - 4) = 0
o
in 2 + 10 * in - 96 = 0.
Questa è un'equazione quadratica standard che deve essere risolta trovando il discriminante:
D = (10) 2 - 4 * 1 * (-96) = 484.
Secondo le formule è necessario fare calcoli per il lato sconosciuto:
in 1 = (- 10 + 22) / 2 = 6 (cm);
in 2 = (- 10 - 22) / 2 = - 16 - questa radice non soddisfa la soluzione del problema, perché il lato non può essere negativo.
Risposta: il lato sconosciuto è 6 cm.
Terzo compito
condizione
In alcuni triangoli sono indicati i lati: a, b, c , che sono rispettivamente di 6 cm, 10 cm e 8 cm. È necessario calcolare l'angolo A.
decisione
Ancora una volta è necessario utilizzare il teorema del coseno. Viene usato il suo record, in cui vi è il coseno dell'angolo A, poiché è proprio questo che deve essere calcolato. Ecco la formula per il coseno di un'angolazione sconosciuta:
Ad
cos А = (in 2 + с 2 - а 2 ) / (2 в * с).
Resta da sostituire i valori delle parti ed eseguire tutti i calcoli:
cos A = (10 2 + 8 2 - 6 2 ) / (2 * 8 * 10).
Dopo tutti i termini sono quadrati e moltiplicando i numeri dal denominatore:
cos A = (100 + 64 - 36) / (160).
Dopo l'aggiunta e la divisione risulta:
cos A = 128/160 = 0,8.
Ora è necessario utilizzare la tabella Bradis per scoprire quale angolo A. è uguale a.Il valore di angolo più vicino per questo coseno è 36 ° 54 '.
Risposta: il valore dell'angolo A è 36º54 '.