Come calcolare la percentuale della quantità dei modi più semplici

Ogni persona nella sua vita quasi ogni giorno si trova di fronte al concetto di interesse. E questo riguarda non solo ottenere un valore percentuale da un numero, ma anche risolvere il problema, come calcolare la percentuale della somma dei numeri. Nella vita di tutti i giorni e nella vita di tutti i giorni, molti non prestano attenzione a questo, tuttavia, tutti questi calcoli sono incorporati in noi dalla panchina della scuola.

Cos'è la percentuale

Per quanto riguarda il concetto di interesse, può essere spiegato nel modo più semplice, senza entrare nei fondamenti dei calcoli matematici. In effetti, la percentuale rappresenta una parte di qualcos'altro. Non importa in quale indicatore verrà espressa la corrispondenza della percentuale con la fonte principale. La cosa principale è capire che una tale rappresentazione può essere nella forma della percentuale stessa (%) o nella forma di una frazione, che alla fine determina il rapporto tra la parte percentuale e la variante originale.

L'uso dell'interesse nella pratica

Come calcolare l'interesse, ognuno di noi conosce di più dal corso di matematica della scuola. Nella vita di tutti i giorni, ci troviamo di fronte a percentuali quasi ogni minuto. Qualsiasi casalinga, preparando un piatto, usa una ricetta in cui viene presentata la percentuale. L'esempio più semplice: prendere mezzo bicchiere di latte ... Questa è l'interpretazione matematica di ciò che costituisce una certa parte in relazione al tutto.

Assolutamente tutti i calcoli sono basati sul 100 percento (100%) o uno (1), se il calcolo sarà effettuato utilizzando le frazioni. Da questo e respinto quando si calcola qualsiasi componente dell'indicatore iniziale.

Lo stesso vale per la domanda su come calcolare la percentuale dell'importo, quando l'indicatore iniziale (100%) non è un numero, ma diversi. Le opzioni di calcolo qui possono essere parecchio. Consideri il più semplice

Calcola percentuale in proporzione

Ora non terremo conto del calcolo dell'interesse utilizzando le stesse tabelle di programmi per ufficio come Excel, che fanno ciò in modalità automatica quando si specifica la formula appropriata.

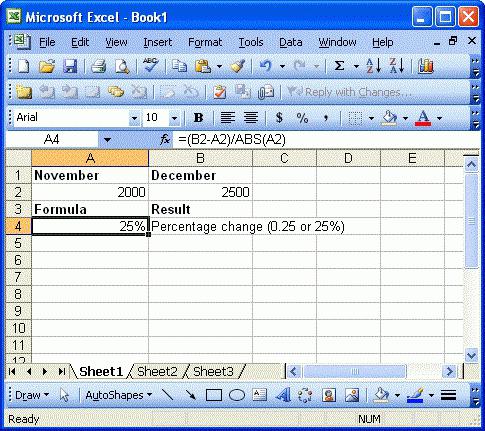
In alcuni casi, viene utilizzata una calcolatrice, in cui è possibile impostare il calcolo di tali azioni. Ma non si tratta di questo ora.

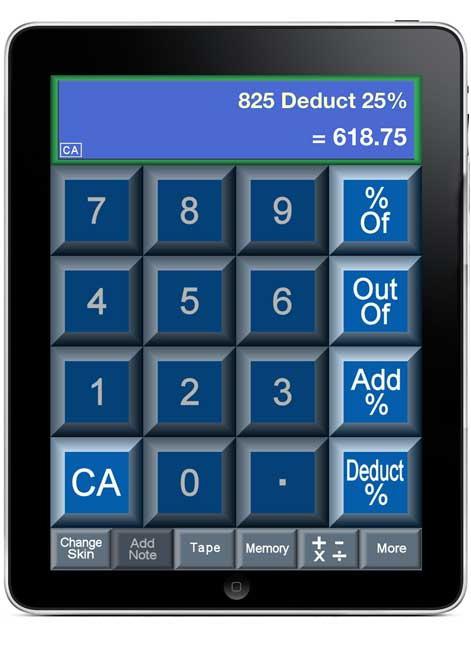
Considera i metodi di calcolo più comuni, che ci sono familiari dal corso di matematica della scuola.

Il modo più semplice e più comune è quello di risolvere le proporzioni.

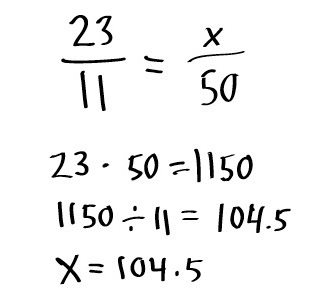
In questo caso, il numero iniziale è impostato al 100% (ad esempio, un numero arbitrario "a") e la sua parte (ad esempio "b") - come "x" sconosciuta. In matematica sembra questo:

a = 100%;

b = x.

In base alle regole della proporzione, puoi calcolare il numero sconosciuto x. Per questo, viene utilizzato il cosiddetto metodo incrociato. In altre parole, è necessario moltiplicare b per 100 e dividere per a. Esattamente la stessa regola si applica se, nel caso della stesura della proporzione, si cambiano b e x in punti, quando la percentuale è nota, ma è necessario calcolare la parte in un'espressione numerica.

Calcolo rapido degli interessi

Certo calcolo degli interessi con l'aiuto della proporzione è fondamentale. Tuttavia, usando numeri frazionari questa procedura è semplificata fino all'impossibilità. Dopo tutto, cos'è il 50% in realtà? Metà. Quello è 1/2 o 0.5 (basato sul numero iniziale 1). Ora è chiaro: per calcolare la metà, è necessario moltiplicare il numero desiderato di 1/2, o di 0,5, o dividere per 2. Questo metodo, tuttavia, è adatto solo per i numeri che sono divisibili senza resto.

Nel caso di caratteri residui o infiniti nel periodo successivo alla virgola come 0.33333333 ... è meglio usare espressioni frazionarie come 1/3. A proposito, le frazioni (in alcuni casi irrazionali) riflettono accuratamente il numero stesso, perché le cifre periodiche dopo la virgola, indipendentemente da quanto tu chiedi, non daranno comunque un numero intero. E così lo stesso terzo esprime chiaramente e chiaramente l'essenza.

Nelle stesse ricette, ovviamente, un terzo può essere determinato, per così dire, a occhio. Ma nei processi chimici, in particolare quelli relativi al dosaggio fine dei componenti, ad esempio nell'industria farmaceutica, questo metodo non funzionerà. Non è necessario fare affidamento sull'occhio. È necessario utilizzare i rapporti esatti degli ingredienti, anche se uno degli indicatori ha la forma di un numero con un numero in un periodo o è rappresentato nella forma della stessa frazione irrazionale. Ma, di regola, per esempio, quando si pesa, tali numeri possono essere limitati a un punto decimale dopo il punto decimale o al massimo un millesimo.

Come calcolare la percentuale dell'importo

Molto spesso si devono trattare diversi numeri richiesti o la loro somma. La questione di come calcolare le percentuali dell'importo è risolta facilmente come nel caso di utilizzo di un numero iniziale singolo. L'unica cosa da considerare in questo caso è la rappresentazione abituale della somma come valore singolo.

Ad esempio, abbiamo due numeri, a e b, e l'indicatore iniziale è il numero d. In questo caso, la proporzione sarà la seguente:

d = 100%;

(a + b) = x.

Si noti che la somma (a + b) può ancora essere rappresentata come un numero singolo. Lascia che sia z. Nel caso in cui impostiamo la formula a + b = z, la proporzione assume una forma completamente standard:

d = 100%;

z = x.

Come puoi vedere, niente di complicato a riguardo.

C'è un'altra opzione quando la somma (a + b) = 100% e d = x.

Qui la soluzione assomiglia a questa:

(dx 100) / (a ​​+ b) o (d / (a ​​+ b)) + 100 / (a ​​+ b).

Come già inteso, qui viene usato il principio del denominatore comune per le frazioni.

Se aggiungiamo a e b, la cui somma è uguale a z, la proporzione ritorna alla forma standard:

z = 100%;

d = x.

Lo stesso vale in ordine inverso.

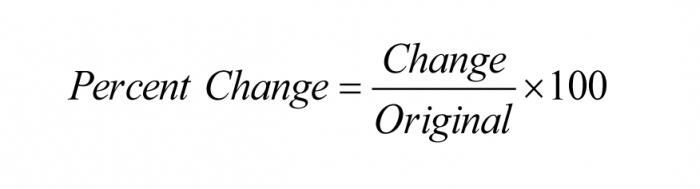
Spiegazione matematica

Dal punto di vista della matematica e dei suoi fondamenti, risolvere il problema di come calcolare una percentuale di una somma si riduce solo all'applicazione delle regole più semplici per espandere le parentesi quando si moltiplica una somma per un singolo numero e si cerca un denominatore comune, che, in generale, è questo. In altre parole, può essere rappresentato in termini di formula come segue:

ax (b + c) = ab + ac ,

dove ab e ac sono prodotti di termini tra parentesi (b e c) di un numero (coefficiente) prima delle parentesi a.

In realtà, lo stesso metodo agisce in proporzione. Supponiamo di avere un certo numero z, che rappresenta il 100%, e la somma dei numeri a e b. La percentuale da calcolare è denotata da un numero sconosciuto y. In questa forma di realizzazione, la proporzione assume la forma:

z = 100%;

(a + b) = y.

Quindi la soluzione semplice:

((a + b) x 100%) / z = ((asse 100%) + (bx 100%)) / z

Tra parentesi le azioni vengono prese per sottolineare che l'operazione di moltiplicazione viene eseguita in primo luogo e l'aggiunta di opere - nel secondo. La stessa azione viene eseguita se inizialmente la somma dei numeri è 100%.

Calcolo inverso

Molto spesso nella questione di come calcolare la percentuale dell'importo, c'è un trasferimento inverso non ambiguo. In pratica, ciò è dovuto, per esempio, al calcolo inverso del trimestre. Tutti sanno che questa cifra è pari al 25% del numero iniziale. Facciamo, per esempio, il prezzo delle merci aumentato del 25%, che ammontava a 25 rubli. Dobbiamo scoprire quanto questo prodotto è diventato. Ora proveremo a capire come calcolare non il numero iniziale, conoscendo il valore percentuale, ma l'intero importo, che dovrebbe risultare alla fine. Sembrerebbe che la soluzione sia semplice:

25 = 25% (1/4 o 0,25);

x = 100%.

No, assolutamente sbagliato. Quindi puoi ottenere solo il numero iniziale, escludendo il 25%. Per calcolare l'intero importo, tenendo conto del 25% è necessario utilizzare la formula:

25 = 25%;

x = 100% + 25%.

O 100 / 0.8, che mostrerà il valore 125 (100 + 25), poiché il 100% più il 25% nell'espressione unitaria è il numero 1.25 (uno più un quarto) e nell'inverso (1 / x) è solo 0,8. Facendo calcoli, otteniamo x = 125.

conclusione

Come puoi vedere, non c'è niente di particolarmente difficile nel modo in cui calcolare la percentuale dell'importo. È vero, nel programma scolastico, la traduzione inversa viene spesso omessa per qualche motivo. Quindi molti contabili che lavorano su rapporti che pagano la stessa IVA hanno spesso problemi.

Quindi devi solo prendere in considerazione le regole di base per il calcolo degli interessi, e i problemi scompariranno da soli.

D'altra parte, per comodità, sia le proporzioni che l'uso delle frazioni possono essere applicate allo stesso modo. Nel primo caso, abbiamo, per così dire, la versione classica, e nella seconda - una soluzione semplice e universale. Ancora una volta, è meglio usarlo nel caso di una divisione senza resto. Ma quando si calcolano le parti più popolari come metà, quarto, terzo ecc., Questo metodo è molto conveniente.

Anche i calcoli inversi, come si può vedere dagli esempi precedenti, non sono complessi. La cosa principale è prendere in considerazione il coefficiente inverso quando si calcola il numero desiderato. Sembra che ora tutto andasse a posto. Come si suol dire, matematica semplice.