Come calcolare il volume di vari corpi geometrici?
Nel corso della stereometria, una delle domande principali è come calcolare il volume di un particolare corpo geometrico. Tutto inizia con un semplice parallelepipedo e termina con una palla.
Anche nella vita, spesso devono affrontare problemi simili. Ad esempio, per calcolare il volume d'acqua che viene posto in un secchio o una botte.
Proprietà giuste per il volume di ogni corpo
- Questo valore è sempre un numero positivo.
- Se il corpo può essere diviso in parti in modo che non vi siano intersezioni, il volume totale è uguale alla somma dei volumi delle parti.
- I corpi uguali hanno lo stesso volume.
- Se un corpo più piccolo si adatta completamente a uno più grande, allora il volume del primo è più piccolo del secondo.
Notazione generale per tutti i corpi
In ognuno di essi ci sono bordi e basi, in cui sono costruite altezze. Pertanto, tali elementi per loro sono ugualmente contrassegnati. Ecco come sono scritti nelle formule. Come calcolare il volume di ciascuno dei corpi - impareremo ulteriormente e applicheremo nuove abilità nella pratica.
Ad
| designazione | chiarificazione |
| e | bordo del corpo dove sono tutti uguali |
| V | volume |
| S 0 | area di base |
| h | l'altezza |
| r | raggio |
Alcune formule hanno altri valori. La loro designazione sarà discussa quando sorga tale necessità.
Prisma, parallelepipedo (dritto e obliquo) e cubo
Questi corpi sono combinati perché sembrano molto simili e le formule per il calcolo del volume sono identiche:
V = S 0 * h.
Solo S 0 sarà diverso. Nel caso di un parallelepipedo, viene calcolato come per un rettangolo o un quadrato. In un prisma, una base può essere un triangolo, un parallelogramma, un quadrilatero arbitrario o un altro poligono.
Per un cubo, la formula è notevolmente semplificata, perché tutte le sue dimensioni sono uguali:
V = a 3 .
Piramide, tetraedro, piramide tronca
Per il primo di questi corpi, esiste una formula del genere per calcolare il volume:
V = 1/3 * S 0 * n.
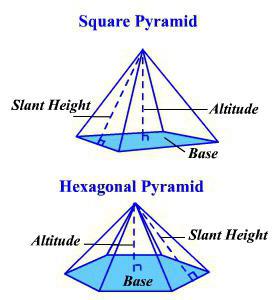
Il tetraedro è un caso speciale di una piramide triangolare. Tutti i bordi in esso sono uguali. Pertanto, otteniamo nuovamente una formula semplificata:
V = (a 3 * √2) / 12, o V = 1/3 S 0 h
La piramide tronca diventa quando la sua parte superiore viene tagliata. Pertanto, il suo volume è uguale alla differenza tra le due piramidi: quella che sarebbe intatta e quella superiore. Se è possibile scoprire entrambe le basi di tale piramide (S 1 è maggiore e S 2 è minore), allora è conveniente usare questa formula per calcolare il volume:
Ad
V = 1/3 * h * (S 1 + √ (S 1 S 2 ) + S 2 ).
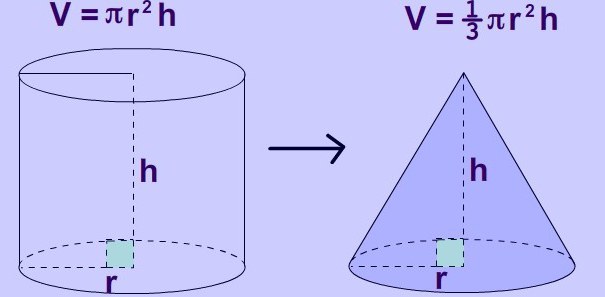
Cilindro, cono e cono troncato
Se vuoi calcolare volume del cilindro È possibile utilizzare la formula specificata per il prisma. A volte è conveniente scriverlo in questa forma:
V = π * r 2 * h.
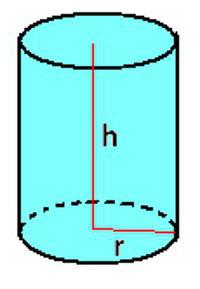
La situazione con il cono è un po 'più complicata. Per lui, c'è una formula:
V = 1/3 π * r 2 * h. È molto simile a quello indicato per il cilindro, solo il valore viene ridotto tre volte.
Proprio come con una piramide tronca, la situazione non è facile con un cono, che ha due basi. La formula per calcolare il volume di un cono troncato è la seguente:
V = 1/3 π * h * (r 1 2 + r 1 r 2 + r 2 2 ). Qui r 1 è il raggio della base inferiore, r 2 è quello superiore (più piccolo).
Palla, segmenti di palla e settore
Queste sono le formule più difficili da memorizzare. per volume della palla lei assomiglia a questo:
V = 4/3 π * r 3 .
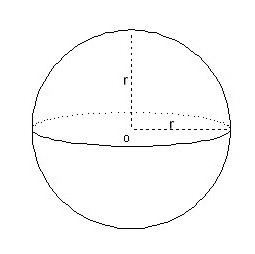
Nei problemi, c'è spesso una questione su come calcolare il volume di un segmento sferico - la parte di una sfera che è, per così dire, tagliata parallelamente al diametro. In questo caso, la seguente formula verrà in soccorso:
V = π h 2 * (r - h / 3). In esso, per h, viene presa l'altezza del segmento, cioè la parte che va lungo il raggio della palla.
Il settore è diviso in due parti: il cono e il segmento della palla. Pertanto, il suo volume è definito come la somma di questi corpi. La formula dopo la trasformazione assomiglia a questo:
V = 2/3 πr 2 * h. Qui h è anche l'altezza del segmento.
Esempi di compiti
Volume del cilindro, della sfera e del cono Pro
Condizione: il diametro del cilindro (1 corpo) è uguale alla sua altezza, il diametro della palla (2 corpo) e l'altezza del cono (3 corpo); controllare la proporzionalità dei volumi V 1 : V 2 : V 3 = 3: 2: 1
La decisione Innanzitutto, è necessario scrivere tre formule per i volumi. Quindi considera che il raggio è metà del diametro. Cioè, l'altezza sarà uguale a due raggi: h = 2r. Dopo aver effettuato una semplice sostituzione, risulta che le formule per i volumi saranno simili a questa:
Ad
V 1 = 2 π r 3 ; V 3 = 2/3 π r 3 . La formula per il volume della palla non cambia, perché l'altezza non appare in essa.
Ora rimane da scrivere le relazioni del volume e fare la riduzione di 2π e r 3 . Si scopre che V 1 : V 2 : V 3 = 1: 2/3: 1/3. Questi numeri portano facilmente a un record 3: 2: 1.
La risposta è V 1 : V 2 : V 3 = 3: 2: 1.
A proposito del volume della palla
Condizione: ci sono due cocomeri con raggio di 15 e 20 cm; Qual è il modo più vantaggioso per mangiarli: i primi quattro o il secondo?
La decisione Per rispondere a questa domanda, devi trovare il rapporto tra i volumi dei pezzi che otterranno da ogni anguria. Tenendo conto che sono palle, è necessario scrivere due formule per i volumi. Poi prendi in considerazione che dal primo ognuno otterrà solo la quarta parte, e dalla seconda - l'ottava.
Ad
Resta da registrare il rapporto tra i volumi delle parti. Sembrerà così:
(V 1 : 4) / (V 2 : 8) = (1/3 π r 1 3 ) / (1/6 π r 2 3 ). Dopo la conversione rimane solo la frazione: (2 r 1 3 ) / r 2 3 . Dopo la sostituzione di valori e calcoli, si ottiene la frazione 6750/8000. Da esso è chiaro che la parte dal primo cocomero sarà inferiore alla seconda.
La risposta è È più vantaggioso mangiare l'ottava parte di un'anguria con un raggio di 20 cm.
A proposito del volume della piramide e del cubo
Condizione: esiste una piramide di argilla con una base rettangolare di 8x9 cm e un'altezza di 9 cm; fecero un cubo dallo stesso pezzo di argilla; com'è il suo vantaggio?
La decisione Se denotiamo i lati del rettangolo con le lettere in e con, allora l'area della base della piramide viene calcolata come il loro prodotto. Quindi la formula per il suo volume:
V 1 = 1/3 * sole * h.
La formula per il volume del cubo è scritta nell'articolo sopra. Questi due valori sono uguali: V 1 = V 2 . Resta da equiparare i lati giusti delle formule e fare i calcoli necessari. Risulta che il bordo del cubo sarà pari a 6 cm.
La risposta è a = 6 cm
Informazioni sul volume parallelepipedo
Condizione: è necessario realizzare una scatola con una capacità di 0,96 m 3 , la sua larghezza e lunghezza sono note - 1,2 e 0,8 metri; Quale dovrebbe essere la sua altezza?
La decisione Poiché la base del parallelepipedo è un rettangolo, la sua area è definita come il prodotto di lunghezza (a) e larghezza (c). Pertanto, la formula per il volume si presenta così:
V = a * c * n.
Da esso è facile determinare l'altezza dividendo il volume per l'area. Risulta che l'altezza dovrebbe essere uguale a 1 m.
La risposta è L'altezza della scatola è di un metro.