Come trovare i numeri primi?

I numeri sono diversi: naturale, naturale, razionale, intero e frazionario, positivo e negativo, complesso e semplice, dispari e pari, reale, ecc. Da questo articolo puoi imparare quali sono i numeri semplici.

Quali numeri sono chiamati la parola inglese "simpl"?

Molto spesso, gli studenti su una delle questioni più semplici a prima vista della matematica, su cosa sia un numero primo, non sanno come rispondere. Spesso confondono numeri semplici con numeri naturali (cioè numeri che le persone usano quando contano gli oggetti, mentre in alcune fonti partono da zero e in altri da uno). Ma queste sono completamente due cose diverse. I numeri primi sono naturali, cioè numeri interi e positivi, che sono più grandi di uno e che hanno solo 2 divisori naturali. In questo caso, uno di questi divisori è un numero dato e il secondo è uno. Ad esempio, tre è un numero primo, poiché non è divisibile per nessun altro numero diverso da se stesso e uno.

Numeri composti

L'opposto dei numeri primi è composto. Sono anche naturali, anche più di uno, ma non ne hanno due, ma un numero maggiore di divisori. Ad esempio, i numeri 4, 6, 8, 9, ecc. Sono numeri naturali, composti, ma non primi. Come puoi vedere, questi sono per lo più numeri pari, ma non tutti. Ma i "due" - un numero pari e "primo numero" nella serie di numeri primi.

sequenza

Per costruire una serie di numeri primi, è necessario fare una selezione tra tutti i numeri naturali, tenendo conto della loro definizione, cioè, è necessario agire al contrario. È necessario considerare ciascuno degli interi positivi per determinare se ha più di due divisori. Proviamo a costruire una serie (sequenza) che compone i numeri primi. L'elenco inizia con due, il successivo è tre, perché è diviso solo in se stesso e in unità. Considera il numero quattro. Ha divisori tranne quattro e uno? Sì, questo numero è 2. Quindi quattro non è un numero primo. Anche Five è semplice (non è divisibile per nessun altro numero tranne 1 e 5), ma sei sono divisibili. E in generale, se segui tutti i numeri pari, puoi vedere che, ad eccezione di "due", nessuno di loro è semplice. Da qui concludiamo che anche i numeri, tranne due, non sono semplici. Un'altra scoperta: tutti i numeri divisibili in tre, ad eccezione della stessa triade, sia essa pari o dispari, non sono neppure semplici (6, 9, 12, 15, 18, 21, 24, 27, ecc.). Lo stesso vale per i numeri che sono divisi in cinque e sette. Tutti loro non sono anche semplici. Riassumiamo. Quindi, le singole cifre sono tutte numeri dispari tranne uno e nove, e da pari - solo "due". Dozzine (10, 20, ... 40, ecc.) Non sono semplici. A due cifre, a tre cifre e così via, i numeri semplici possono essere determinati sulla base dei principi sopra delineati: se non hanno altri divisori oltre a se stessi e a quelli.

Teorie sulle proprietà dei numeri primi

Esiste una scienza che studia le proprietà degli interi, inclusi i numeri primi. Questo è un ramo della matematica, che è chiamato il più alto. Oltre alle proprietà degli interi, si occupa anche di numeri algebrici, trascendentali, nonché di funzioni di varia origine associate all'aritmetica di questi numeri. In questi studi, oltre ai metodi elementari e algebrici, vengono utilizzati anche analitici e geometrici. Nello specifico, lo studio dei numeri primi coinvolti nella teoria dei numeri.

I numeri primi sono i "mattoni" dei numeri naturali.

In aritmetica c'è un teorema, che è chiamato il principale. Secondo questo, qualsiasi numero naturale, tranne uno, può essere rappresentato come un prodotto i cui fattori sono numeri semplici, e l'ordine di sequenza dei fattori è unico, questo significa che il modo di rappresentazione è unico. Si chiama la decomposizione di un numero naturale in fattori primi. C'è un altro nome per questo processo: la fattorizzazione dei numeri. Procedendo da questo, numeri semplici possono essere chiamati "materiale da costruzione", "blocchi" per la costruzione di numeri naturali.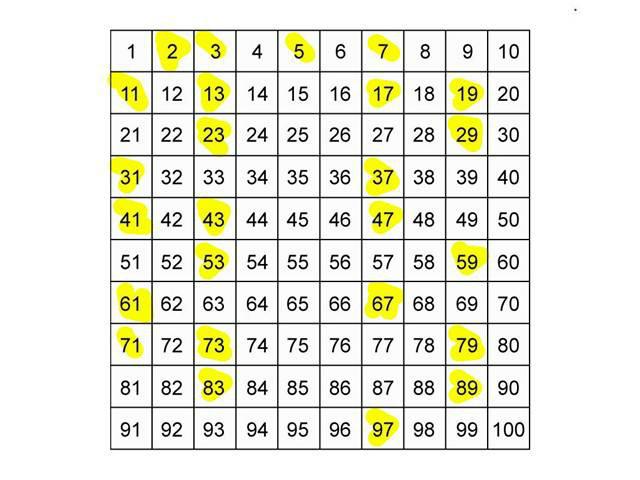

Cerca i numeri primi. Test di semplicità

Molti scienziati di epoche diverse hanno cercato di trovare alcuni principi (sistemi) per trovare una lista di numeri primi. La scienza conosce sistemi che vengono chiamati il ​​setaccio Atkin, il setaccio di Sundartam e il setaccio di Eratostene. Tuttavia, non forniscono alcun risultato significativo e viene utilizzato un semplice controllo per trovare i numeri primi. Inoltre, i matematici hanno creato algoritmi. Sono chiamati test di semplicità. Ad esempio, c'è un test sviluppato da Rabin e Miller. È usato dai crittografi. Esiste anche un test Kayal-Agraval-Sasken. Tuttavia, nonostante la sua precisione sufficiente, è molto difficile da calcolare, il che riduce il suo valore pratico.

L'insieme dei numeri primi ha un limite?

Il fatto che l'insieme del semplice sia l'infinito, ha scritto nel libro "Principles", l'antico studioso greco Euclide. Ha detto questo: "Immaginiamo per un momento che i numeri primi abbiano un limite. Quindi moltiplichiamo l'uno con l'altro e ne aggiungiamo uno al prodotto. Il numero ottenuto come risultato di queste semplici azioni non può essere diviso in uno di un numero di numeri primi, perché ce ne sarà sempre uno nel resto. E questo significa che c'è un altro numero che non è ancora incluso nella lista dei numeri primi. Pertanto, la nostra ipotesi non è vera, e questo set non può avere un limite. Oltre alla prova di Euclide, c'è una formula più moderna data dal matematico svizzero del XVIII secolo, Leonard Euler. Secondo lui, la somma inversa alla somma dei primi n numeri cresce senza limiti al crescere del numero n. Ma la formula del teorema sulla distribuzione dei numeri primi: (n) cresce come n / ln (n).

Qual è il maggior numero primo?

Lo stesso Leonard Eulero riuscì a trovare il più grande primo per il suo tempo. Questo è 2 ³¹ - 1 = 2147483647. Tuttavia, entro il 2013, è stato calcolato l'altro più accurato nell'elenco dei numeri primi, 2 ^57885161 - 1, chiamato numero di Mersenne. Contiene circa 17 milioni di cifre decimali. Come puoi vedere, il numero trovato dagli scienziati del diciottesimo secolo è molte volte più piccolo di questo. Doveva essere così, perché Euler stava facendo questo calcolo manualmente, ma il nostro computer è stato probabilmente aiutato dal nostro contemporaneo. Inoltre, questo numero è stato ottenuto presso la facoltà di matematica in una delle facoltà americane. I numeri, che prendono il nome da questo scienziato, passano attraverso il test di semplicità Luke-Lemere. Tuttavia, la scienza non vuole fermarsi qui. La Electronic Frontier Foundation, fondata nel 1990 negli Stati Uniti d'America (EFF), ha nominato un premio in denaro per la ricerca di grandi numeri primi. E se fino al 2013 il premio è stato fatto valere da quegli scienziati che li avrebbero trovati tra 1 e 10 milioni di numeri decimali, oggi questa cifra ha raggiunto da 100 milioni a 1 miliardo. La dimensione dei premi varia da 150 a 250 mila dollari USA.

Nomi di numeri primi speciali

Quei numeri che sono stati trovati grazie agli algoritmi creati da uno o un altro scienziato e hanno superato il test della semplicità, sono chiamati speciali. Ecco alcuni di loro:

1. Merssen.

2. Wooda.

3. Fattoria.

4. Cullen.

5. Prota.

6. Mills et al.

La semplicità di questi numeri, nominati dopo gli scienziati di cui sopra, è stabilita usando i seguenti test:

1. Luc-Lemer.

2. Pipino.

3. Rizel.

4. Billhart - Lemera - Selfridge, ecc.

La scienza moderna non si ferma qui ed è probabile che nel prossimo futuro il mondo conoscerà i nomi di coloro che potrebbero ricevere un premio di $ 250.000, trovando il maggior numero primo.