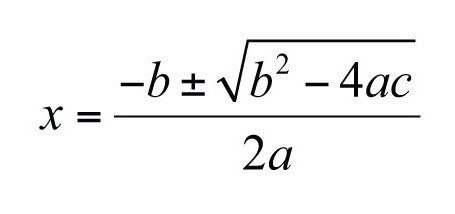Come trovare la radice dell'equazione: lineare, quadratica, cubica?
Le equazioni in matematica sono importanti quanto i verbi in russo. Senza la capacità di trovare la radice di un'equazione, è difficile sostenere che uno studente abbia seguito un corso di algebra. Inoltre, per ciascuna delle loro specie ci sono le loro soluzioni specifiche.
Cos'è?
Un'equazione è costituita da due espressioni arbitrarie contenenti variabili con un segno di uguale tra loro. Inoltre, il numero di quantità sconosciute può essere arbitrario. Il numero minimo è uno.
Per risolverlo è scoprire se esiste una radice dell'equazione. Questo è un numero che lo trasforma nella corretta uguaglianza. In caso contrario, la risposta è l'affermazione che "non ci sono radici". Ma può essere il contrario quando la risposta è una moltitudine di numeri.
Ad
Che tipo di equazioni esistono?
Lineare. Contiene una variabile il cui grado è uguale a uno.
- Square. Una variabile resiste con una potenza di 2, o una trasformazione ha come risultato un tale grado.
- Equazione di altissimo livello
- Razionale frazionale. Quando la variabile è al denominatore della frazione.
- Con modulo
- Irrazionale. Cioè, uno che contiene una radice algebrica.
Come si risolve un'equazione lineare?
È il principale. Per questa visione tutti gli altri cercano di condurre. Dal momento che è facile trovare la radice dell'equazione.
- Innanzitutto, è necessario eseguire le possibili trasformazioni, ovvero espandere le parentesi e fornire termini simili.
- Sposta tutti i monomiali con variabile sul lato sinistro dell'equazione, lasciando i termini liberi sulla destra.
- Porta termini simili in ogni parte dell'equazione da risolvere.
- Nell'uguaglianza risultante nella sua metà sinistra ci sarà il prodotto di un coefficiente e una variabile, e nella metà destra ci sarà un numero.
- Resta da trovare la radice dell'equazione, dividendo il numero sulla destra, per il coefficiente di fronte all'ignoto.
Come trovare le radici di un'equazione quadratica?
Innanzitutto, deve essere ridotto a un modulo standard, ovvero, tutte le parentesi devono essere aperte, devono essere introdotti termini simili e tutti i monomiali devono essere spostati sul lato sinistro. Sul lato destro dell'uguaglianza, dovrebbe rimanere solo zero.
- Usa la formula discriminante. Squadrando il coefficiente prima dell'ignoto con il grado "1". Moltiplicare il numero monomiale libero e il numero davanti alla variabile nel quadrato con il numero 4. Sottrarre il prodotto dal quadrato risultante.
- Stimare il valore del discriminante. È negativo - la decisione è finita, poiché non ha radici. Uguale a zero: la risposta è un numero. Positivo: due valori della variabile.
Trova le due radici dell'equazione in base alla formula in cui radice quadrata dal discriminante deve essere sottratto o aggiunto al coefficiente negativo della variabile di primo grado. Quindi dividere per doppio il coefficiente di fronte al quadrato dell'ignoto. (In caso di parità del discriminante, lo zero dovrà essere aggiunto o sottratto, quindi le due radici coincideranno).
Come risolvere un'equazione cubica?
Prima trova la radice dell'equazione x. È determinato dal metodo di selezione dei numeri che sono i divisori del termine libero. Questo metodo è utile per prendere in considerazione un esempio specifico. Lascia che l'equazione sia: x 3 - 3x 2 - 4x + 12 = 0.
Il suo termine libero è 12. Quindi i divisori che devono essere controllati saranno numeri positivi e negativi: 1, 2, 3, 4, 6 e 12. La ricerca può essere completata sul numero 2. Dà la vera uguaglianza nell'equazione. Cioè, il suo lato sinistro risulta essere zero. Quindi il numero 2 è il primo radice cubica le equazioni.
Ad
Ora devi dividere l'equazione originale per la differenza tra la variabile e la prima radice. In un esempio specifico, questo è (x - 2). Una semplice trasformazione porta il numeratore a tale fattorizzazione: (x - 2) (x + 2) (x - 3). Gli stessi fattori del numeratore e del denominatore sono ridotti, e le rimanenti due parentesi nella descrizione forniscono una semplice equazione quadratica: x 2 - x - 6 = 0.
Qui trovi le due radici dell'equazione secondo il principio descritto nella sezione precedente. Sono i numeri: 3 e -2.
Quindi, un'equazione cubica concreta ha tre radici: 2, -2 e 3.
Come i sistemi sono risolti equazioni lineari?
Qui viene proposto un metodo per eliminare le incognite. Consiste nell'esprimere uno sconosciuto attraverso l'altro in una equazione e sostituire questa espressione in un'altra. Inoltre, la soluzione di un sistema di due equazioni con due incognite è sempre una coppia di variabili.
Ad
Se le variabili in esse sono indicate dalle lettere x 1 e x 2 , allora possiamo derivare dalla prima equazione, per esempio x 2 . Quindi viene sostituito nel secondo. La trasformazione necessaria è effettuata: divulgazione di parentesi e coercizione di membri simili. Risulta una semplice equazione lineare, la cui radice è facile da calcolare.
Ora torna alla prima equazione e trova la radice dell'equazione x 2 , usando l'equazione risultante. Questi due numeri sono la risposta.
Semplice consiglio
Per essere sicuri della risposta ricevuta, si consiglia di effettuare sempre un controllo. Non è necessario scrivere.
Se un'equazione è risolta, allora ciascuna delle sue radici deve essere sostituita nell'uguaglianza originale e ottenere gli stessi numeri in entrambe le sue parti. Tutto è venuto insieme - la decisione giusta.
Quando si lavora con il sistema, è necessario sostituire le radici in ciascuna soluzione ed eseguire tutte le azioni possibili. Risulta l'uguaglianza corretta? Quindi la decisione è corretta.