Come trovare il volume di un cubo: opzioni per i problemi e la loro soluzione
Le moderne tecnologie creano incredibili programmi per computer. Ti permettono di vedere il corpo in volume e ruotarlo in direzioni diverse per ottenere un aspetto migliore. L'immaginazione dell'uomo non è sempre in grado di farlo. Pochi possono chiaramente presentare il soggetto e vederlo attraverso. Ma una tale abilità può essere tentata di formarsi quando si risolvono problemi in geometria. Ad esempio, quelli che parlano di come trovare il volume di un cubo. Questa è una pratica eccellente per lo sviluppo dell'immaginazione spaziale.
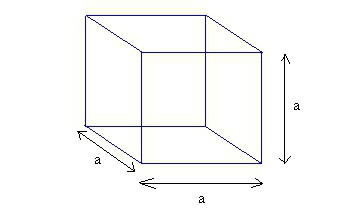
Cubo o parallelepipedo?
Questa è una domanda non vuota. Perché la classificazione è importante. Dopo tutto, un cubo è una forma speciale di parallelepipedo rettangolare.
Quest'ultima è una figura in cui ci sono 6 volti, e tutti sono rettangoli. Angoli in cui tutti i bordi si intersecano, 90º. Di conseguenza, se queste facce diventano quadrati, allora l'intera figura sarà trasformata in un cubo.
Ad

In un parallelepipedo rettangolare, tutte le quote lineari, ovvero altezza, lunghezza e larghezza, possono differire in modo significativo. Nel cubo, sono sempre uguali tra loro. Questo è il suo segno distintivo. Pertanto, nei compiti che richiedono di trovare il volume di un cubo, il momento considerato viene sicuramente preso in considerazione. A proposito, semplifica enormemente tutti i record e i calcoli matematici.
Convenzioni in formule e problemi
Senza questo elemento sarà difficile capire come vengono scritte le formule. Cosa si intende per ogni lettera e simbolo, richiede la seguente tabella.
| simbolo | Nome dell'oggetto |
| e | forma di costola |
| d | faccia diagonale |
| D | cubo diagonale |
| simboli geometrici comuni | zona |
| volume |
Come trovare gli elementi del cubo dalla sua parte?
Poiché la faccia della figura è un quadrato, la sua area è determinata dalla formula n. 1, in cui un valore noto deve essere quadrato:
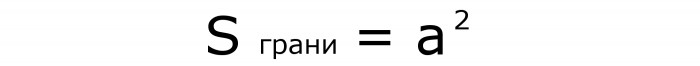
E la diagonale di qualsiasi faccia è calcolata dalla formula n. 2, in cui il lato è moltiplicato per la radice di 2:
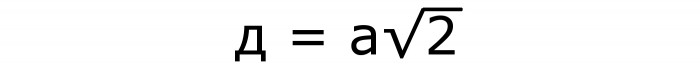
La formula precedente è ottenuta dal teorema di Pitagora. Questo è facile da capire se vedi che la diagonale del volto è l'ipotenusa triangolo rettangolo. E i lati della piazza diventano le sue gambe.
Per determinare la diagonale di un cubo, sarà necessaria la seguente formula n. 3, contenente un lato noto e radice quadrata da 3:
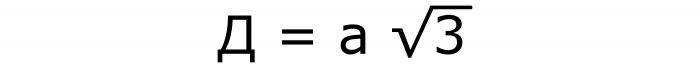
È anche ottenuto dal teorema di Pitagora. Solo come ipotenusa agisce la diagonale desiderata. Il lato del quadrato e la sua diagonale diventano le gambe.
A volte è necessario conoscere la formula per calcolare l'area della superficie laterale di questa figura. In esso, il quadrato del lato viene moltiplicato per 4. Eccolo (n. 4):
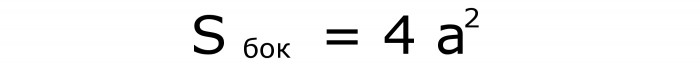
Capire come funziona questa formula è facile. Ci sono 4 facce laterali - 4. Ciò significa che la loro area totale è un valore quadruplo dell'area di un quadrato.
Se è necessario determinare l' area dell'intera superficie , quindi utilizzare questo record, in cui viene utilizzato il quadrato della costola (formula n. 5):
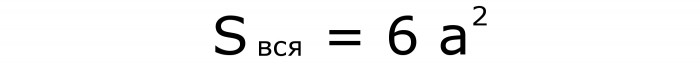
È ottenuto in modo simile alla formula precedente, solo il numero di quadrati è aumentato a 6.
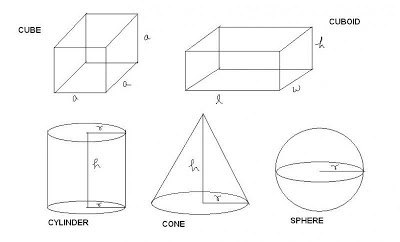
Cos'è il volume?
In poche parole, questo è il luogo che prende qualsiasi corpo nello spazio. Qualsiasi oggetto è limitato nello spazio dalle superfici. Potrebbero esserci diversi, ma ci possono essere casi in cui solo uno. Ad esempio, se il corpo è una palla. Ma queste superfici sono necessariamente chiuse. Lo spazio occupato da un corpo geometrico sarà la sua capacità o volume.
Ad
Unità di volume
Quando si tratta di solidi, le unità di volume saranno sempre valori cubici. Ad esempio, un metro, un centimetro o un chilometro in un cubo. Per i liquidi si usano litri, che sono espressi in decimetri cubici. Ma se occupano volumi molto grandi, vengono misurati anche in metri cubi. Ad esempio, se si tiene conto del consumo di acqua in un appartamento, viene considerato in m 3 . Quindi risulta più conveniente e più semplice in termini numerici.
Metodo 1: trova il volume del cubo, se noto
Questo è il metodo più semplice per dirti come trovare il volume di un cubo. È semplicemente aumentare il valore della festa in un terzo grado. In altre parole, devi moltiplicare il lato da solo tre volte. Per analogia con un parallelepipedo rettangolare arbitrario, quando era necessario moltiplicare tutte le sue dimensioni lineari. La formula sarà scritta come segue (n. 6):
Ad
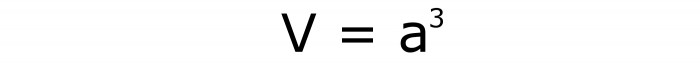
Metodo 2: l'intera area della superficie è nota
In questo caso, dovrai dividere il valore noto per 6. Dalla risposta intermedia, estrai la radice quadrata e alza il numero nel cubo. Se scriviamo questa formula, otteniamo quanto segue (# 7):
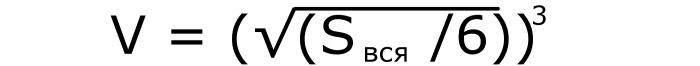
Metodo 3: data la faccia diagonale del cubo
Per scoprire come calcolare il volume di un cubo, in questo caso, è necessario eseguire i seguenti passaggi. Innanzitutto, crea un valore noto in un cubo, quindi moltiplicalo per la radice quadrata di 2 e dividi per 4. La formula per questo problema (N. 8):
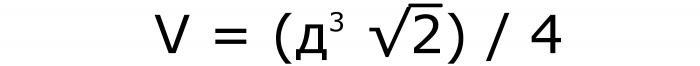
Questa equazione è ottenuta in questo modo: la diagonale nota deve essere divisa per la radice dei due. Quindi costruire il numero al terzo grado. Dopo aver eseguito le trasformazioni, il cubo della diagonale si ottiene nel numeratore e 2 √ 2 nel denominatore. La matematica richiede che non ci sia un numero irrazionale sotto la linea. Pertanto, si liberano di esso moltiplicando per √2. Quindi √2 appare nel numeratore e 4 è ottenuto nel denominatore.
Ad
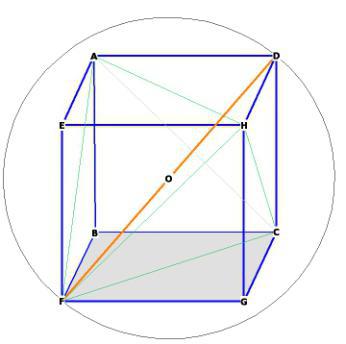
Metodo 4: cubo diagonale
La formula che ti dice come trovare il volume di un cubo conterrà le azioni: quadrando la diagonale, moltiplicandola per la radice di 3 e dividendo per solo 9. Sarà scritta così (n. 9):
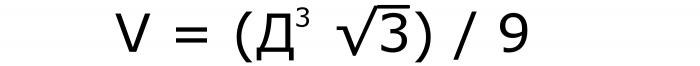
Simile alla formula precedente, in questo record, la diagonale viene prima divisa nella radice di tre e rialzata in un cubo. Dopo le trasformazioni al denominatore, appare anche l'irrazionalità, da cui è necessario partire. Pertanto, il valore √3 appare nel numeratore e sotto la linea - 9.
Esempi di attività
Compito uno. Viene fornito un cubo con un bordo di 12 cm. Calcola il suo volume ed esprime la risposta in metri quadrati.
In questo compito, sarà più difficile tradurre la risposta in altre unità che decidere come trovare il volume di un cubo. Per completare la prima parte dell'attività, è necessaria la formula scritta sotto il numero 6. Dopo che il numero 12 è stato incorporato nel cubo, la risposta sarà 1728 cm 3 . Ora dobbiamo ricordare come tradurli in metri cubi. A tale scopo, la risposta deve essere divisa in 100 tre volte. Un centinaio proveniva dal fatto che era di cento centimetri a un metro. E la divisione viene eseguita tre volte, poiché le unità nell'attività sono cubiche. Quindi, 1728 diviso per 100 darà 17.28. Dopo la seconda divisione sarà 0.1728. La terza azione darà la risposta 0,001728 m 3 . Questa è la risposta al problema: il volume del cubo è 0.001728 m 3 .
Ad
Compito due. C'è un cubo con un'area della sua intera superficie pari a 600 dm 2 . Trova il volume della forma ed esprimilo in metri cubi.
Per rispondere alla domanda di questo compito, sarà necessaria la formula numero 7. La prima azione è un numero noto diviso per 6. La risposta produce 100. È facile estrarre la radice quadrata da esso, sarà 10. Ora è necessario costruire la top ten in un cubo. Quindi risulta che il valore desiderato è uguale a 1000 dm 3 . Resta da convertire in m 3 . Come nel compito precedente, la divisione verrà eseguita tre volte, solo il divisore sarà 10. Perché ci sono dieci decimetri in un metro. Dopo la divisione, la risposta è 1 m 3 . Risposta: il volume è 1 m 3 .
Il terzo compito. Dato un cubo con una lunghezza diagonale della sua faccia uguale a √2 mm. Hai bisogno di calcolare il volume.
L'ottava formula ti aiuterà a trovare la risposta in questo problema. La prima cosa che devi costruire un cubo con un valore noto. La radice quadrata di 2 nel terzo grado darà il valore 2√2. Dopo aver moltiplicato per √2, otteniamo il numero 4. L'ultima azione è dividerla per 4. Risposta: il volume del cubo è 1 mm 3 .
Il quarto compito. È noto che la diagonale di un cubo è di 3 m. È necessario per calcolarne il volume.
Sarà facile trovare la risposta a questo problema usando la formula numero 9. Il valore indicato nella condizione deve essere elevato a un cubo. Risulta 27. Dopo averlo diviso per 9, la risposta sarà 3. E l'ultima azione dovrebbe essere moltiplicata per la radice quadrata di 3. La risposta del problema sarà 3√3 m 3 .