Introduzione alla programmazione dinamica

Tra i problemi risolti con l'aiuto della programmazione matematica, possiamo individuare una classe separata di problemi che richiedono l'ottimizzazione di processi multi-fase (multi-stage). Tali compiti si distinguono per la capacità di suddividere la soluzione in diversi passaggi correlati. Per risolvere tali problemi, viene utilizzata la programmazione dinamica o, come viene anche chiamata, la programmazione multistadio. I suoi metodi sono ottimizzati per trovare la soluzione ottimale di problemi a più fasi, che possono essere suddivisi in più fasi, passaggi, ecc.

Origine del termine

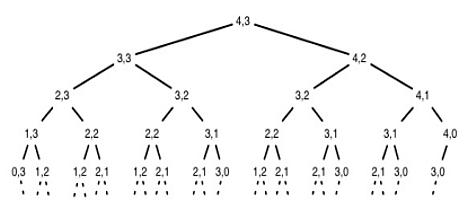
L'uso della parola "dinamico" nel titolo inizialmente presupponeva che la divisione in sottoattività si sarebbe verificata principalmente nel tempo. Quando si utilizzano metodi dinamici per risolvere la produzione, il business e altri compiti, in cui è coinvolto il fattore tempo, la suddivisione in fasi separate non è difficile. Ma è possibile utilizzare la tecnica della programmazione dinamica in attività in cui le singole fasi non sono correlate nel tempo. Sempre in un'attività a più fasi, è possibile selezionare un parametro o una proprietà, in base al quale è possibile dividere in passaggi separati.

Algoritmo (metodo) per risolvere problemi a più stadi

Algoritmo o Il metodo di programmazione dinamica si basa sull'utilizzo del principio dell'ottimizzazione sequenziale del problema, quando la soluzione di un problema generale è suddivisa in un numero di soluzioni di singole attività secondarie con successiva integrazione in un'unica soluzione. Molto spesso, le singole sottoattività sono le stesse e una soluzione comune riduce significativamente il tempo di calcolo. 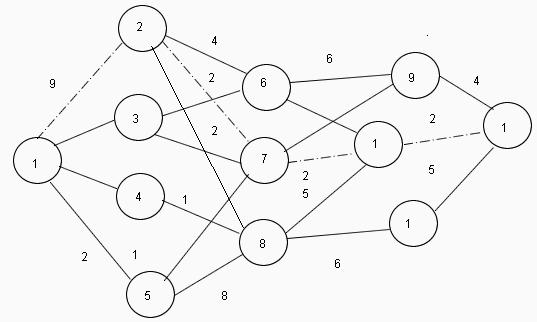Una caratteristica del metodo è l'autonomia di risolvere il problema in ogni fase separata, vale a dire, indipendentemente da come il processo è stato ottimizzato e risolto nella fase precedente, il calcolo corrente utilizza solo i parametri di processo che lo caratterizzano al momento. Ad esempio, un conducente che guida su una strada decide il turno corrente, indipendentemente da quanto o quanto abbia guidato prima.

Metodo sopra e metodo sotto

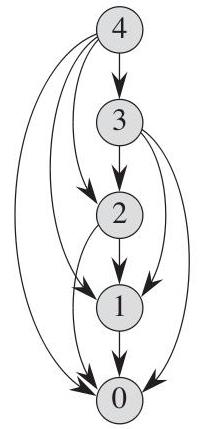
Nonostante il fatto che quando si calcola in una fase separata di risoluzione di un problema, vengono utilizzati i parametri di processo per il momento corrente, il risultato dell'ottimizzazione nella fase precedente influenza i calcoli delle fasi successive per ottenere il miglior risultato in generale. La programmazione dinamica chiama tale principio di decisione il metodo di ottimalità, che determina che la strategia ottimale per risolvere un problema, indipendentemente dalle decisioni e dalle condizioni iniziali, deve costituire una strategia ottimale per lo stato iniziale nelle fasi successive. Come si vede, il processo di risoluzione di un problema è una continua ottimizzazione del risultato in ogni fase separata dal primo all'ultimo. Questo metodo è chiamato il metodo di programmazione top. La figura mostra schematicamente l'algoritmo della soluzione dall'alto verso il basso. Ma esiste una classe di problemi multistep in cui l'effetto massimo è già noto nell'ultima fase, ad esempio, siamo già arrivati ​​dal punto A al punto B e ora vogliamo sapere se siamo andati correttamente in ogni fase precedente o se potevamo fare qualcosa in modo più ottimale. Una sequenza ricorsiva di stadi sorge, cioè andiamo come se "dal contrario". Questo metodo di soluzione è chiamato "metodo di programmazione inferiore".

Applicazione pratica

La programmazione dinamica può essere utilizzata in qualsiasi campo di attività dove ci sono processi che possono essere su qualsiasi parametro (tempo, quantità, temperatura, ecc.) divisi in un numero di piccoli stadi identici. I metodi di soluzione dinamica più ampiamente usati sono stati ottenuti nella teoria del controllo e nello sviluppo di sistemi di calcolo.

Cerca il percorso migliore

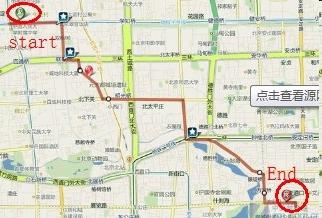
Usando l'ottimizzazione dinamica, è possibile risolvere una vasta classe di problemi nel trovare o ottimizzare il percorso più breve e altri problemi in cui il metodo "classico" di elencare le possibili soluzioni porta ad un aumento del tempo di calcolo, e talvolta è generalmente inaccettabile. Il classico problema della programmazione dinamica è un problema di zaino: viene dato un certo numero di oggetti con una certa massa e costo, ed è necessario scegliere un insieme di oggetti con un valore massimo e una massa che non superi il volume dello zaino. La classica enumerazione di tutte le opzioni alla ricerca della soluzione ottimale richiederà molto tempo e, con l'aiuto di metodi dinamici, il problema verrà risolto in un tempo ragionevole. I compiti di trovare il percorso più breve per la logistica dei trasporti sono fondamentali e i metodi di soluzione dinamici sono perfettamente adatti alla loro soluzione. L'esempio più semplice di tale compito è la costruzione del percorso più breve da parte di un navigatore GPS per auto.

produzione

La programmazione dinamica è ampiamente utilizzata nella risoluzione di vari compiti di produzione, come la gestione dell'inventario per mantenere il numero richiesto di componenti in qualsiasi momento, la pianificazione del processo di produzione, la manutenzione e revisione delle attrezzature, il carico uniforme del personale, l'allocazione più efficiente dei fondi di investimento, ecc. Per risolvere i problemi di produzione utilizzando metodi di programmazione dinamica, sono stati sviluppati pacchetti software speciali e Integrato in sistemi di gestione aziendale conosciuti come SAP.

Campo scientifico

I metodi di programmazione dinamica sono ampiamente utilizzati in vari studi scientifici. Ad esempio, sono utilizzati con successo negli algoritmi di riconoscimento vocale e di immagine, nell'elaborazione di grandi matrici di dati in sociologia e attività economica.