Punto materiale: definizione, valori, esempi e risoluzione dei problemi

Qual è il punto materiale? A quali quantità fisiche sono associate, per cui viene generalmente introdotto il concetto di un punto materiale? In questo articolo discuteremo di questi problemi, forniremo esempi di problemi associati al concetto in discussione e parleremo anche delle formule utilizzate per risolverli.

definizione

Allora, qual è il punto materiale? Diverse fonti danno una definizione in uno stile letterario leggermente diverso. Lo stesso vale per gli insegnanti di università, college e istituti scolastici. Tuttavia, secondo lo standard, un punto materiale è chiamato corpo, le cui dimensioni (rispetto alle dimensioni del telaio di riferimento) possono essere trascurate.

Connessione con oggetti reali

Sembrerebbe, come puoi prendere una persona, un ciclista, un'auto, una nave e persino un aeroplano come punto materiale, che sono per lo più affrontati in problemi di fisica quando si tratta dei meccanismi di un corpo in movimento? Guardiamo più in profondità! Per determinare le coordinate di un corpo in movimento in qualsiasi momento, è necessario conoscere diversi parametri. Questa è la coordinata iniziale, la velocità di movimento e l'accelerazione (se, ovviamente, ha luogo) e il tempo.

Cosa è necessario per risolvere i problemi con i punti materiali?

Le relazioni di coordinate possono essere trovate solo collegandosi al sistema di coordinate. Il nostro pianeta sta diventando un tipo di sistema di coordinate per un'auto e un altro corpo. E in confronto alle sue dimensioni, la dimensione del corpo può essere davvero trascurata. Di conseguenza, se prendiamo il corpo come punto materiale, la sua coordinata è bidimensionale (tridimensionale) spazio può e dovrebbe essere trovato come la coordinata di un punto geometrico.

Il movimento del punto materiale. compiti

A seconda della complessità, le attività possono acquisire determinate condizioni. Di conseguenza, in base alle condizioni date, possiamo usare certe formule. A volte, anche con l'intero arsenale di formule, non è ancora possibile risolvere il problema, come si suol dire, "testa a testa". Pertanto, è estremamente importante non solo conoscere le formule cinematiche relative al punto materiale, ma anche essere in grado di usarle. Cioè, per esprimere il valore desiderato ed equare il sistema di equazioni. Ecco le formule di base che applicheremo nel corso della risoluzione dei problemi:

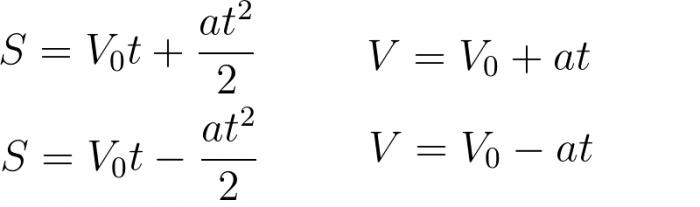
Problema numero 1

L'auto, in piedi sulla linea di partenza, inizia bruscamente a muoversi da una posizione stazionaria. Scopri a che ora accelera a 20 metri al secondo, se la sua accelerazione è di 2 metri al secondo al quadrato.

Voglio solo dire che questo compito è praticamente la cosa più semplice che uno studente possa aspettarsi. La parola "praticamente" sta qui per una ragione. Il fatto è che può essere più semplice sostituire semplicemente i valori diretti in formule. Dovremmo prima esprimere il tempo e poi fare i calcoli. Per risolvere il problema, abbiamo bisogno della formula per determinare la velocità istantanea (la velocità istantanea è la velocità del corpo in un determinato momento). Ha la seguente forma:

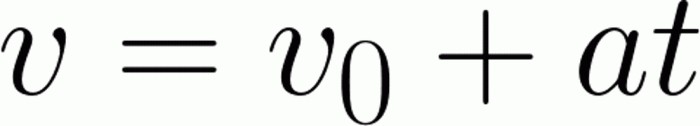
Come possiamo vedere, sul lato sinistro dell'equazione abbiamo velocità istantanea. Non ne abbiamo assolutamente bisogno lì. Pertanto, eseguiamo semplici operazioni matematiche: lasciamo il prodotto dell'accelerazione per un po 'sul lato destro e trasferiamo la velocità iniziale a sinistra. Allo stesso tempo, dovresti seguire attentamente i segni, dal momento che un segno lasciato in modo errato può cambiare radicalmente la risposta al compito. Successivamente, complichiamo leggermente l'espressione, eliminando l'accelerazione sul lato destro: dividi per esso. Di conseguenza, a destra, dovremmo avere tempo puro, a sinistra, un'espressione a due livelli. Il tutto è appena scambiato per sembrare familiare. Resta solo da sostituire i valori. Quindi, si scopre che l'auto accelererà in 10 secondi. Importante: abbiamo risolto il problema, supponendo che un punto materiale sia nell'auto.

Problema numero 2

Il punto materiale inizia la frenata di emergenza. Determina quale era la velocità iniziale al momento della frenata di emergenza, se passavano 15 secondi prima di un arresto completo del corpo. L'accelerazione è pari a 2 metri al secondo al quadrato.

Il compito, in linea di principio, è abbastanza simile a quello precedente. Ma ci sono un paio delle loro sfumature. Per prima cosa, dobbiamo determinare la velocità, che di solito chiamiamo la velocità iniziale. Cioè, ad un certo punto, inizia il conto alla rovescia del tempo e della distanza percorsa dal corpo. La velocità in questo caso ricadrà effettivamente sotto questa definizione. La seconda sfumatura è un segno di accelerazione. Ricorda che l'accelerazione è una quantità vettoriale. Di conseguenza, a seconda della direzione, cambierà il suo segno. L'accelerazione positiva è osservata se la direzione della velocità del corpo coincide con la sua direzione. In poche parole, quando il corpo accelera. Altrimenti (cioè nella nostra situazione di frenata), l'accelerazione sarà negativa. E questi due fattori devono essere considerati per risolvere questo problema:

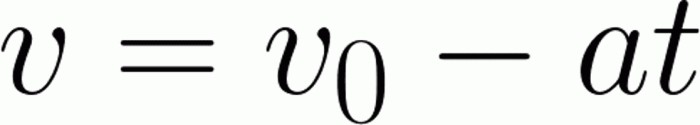
Come l'ultima volta, per prima cosa esprimiamo il valore di cui abbiamo bisogno. Per evitare di fare scherzi con i segni, lasciamo la velocità iniziale dov'è. Con il segno opposto, trasferiamo all'altra parte dell'equazione il prodotto dell'accelerazione in base al tempo. Finita la frenata, la velocità finale è di 0 metri al secondo. Sostituendo questi e altri valori, troviamo facilmente la velocità iniziale. Sarà pari a 30 metri al secondo. È facile notare che, conoscendo le formule, non è così difficile far fronte ai compiti più semplici.

Problema numero 3

Ad un certo punto nel tempo, i dispatcher iniziano a seguire il movimento di un oggetto aereo. La sua velocità in questo momento è di 180 chilometri all'ora. Dopo un periodo di tempo pari a 10 secondi, la sua velocità aumenta a 360 chilometri all'ora. Determina la distanza percorsa in aereo durante il volo, se il tempo di volo era di 2 ore.

In effetti, in senso lato, questo compito ha molte sfumature. Ad esempio, l'accelerazione dell'aereo. È chiaro che il nostro corpo non potrebbe muoversi in linea di principio lungo una traiettoria rettilinea. Cioè, ha bisogno di decollare, prendere velocità, e quindi, a una certa altezza, un segmento della distanza dovrebbe muoversi in linea retta. Le deviazioni non vengono prese in considerazione, così come il rallentamento dell'aeromobile durante l'atterraggio. Ma non è affar nostro in questo caso. Pertanto, risolveremo il problema nell'ambito della conoscenza della scuola, informazioni generali sul movimento cinematico. Per risolvere il problema, abbiamo bisogno della seguente formula:

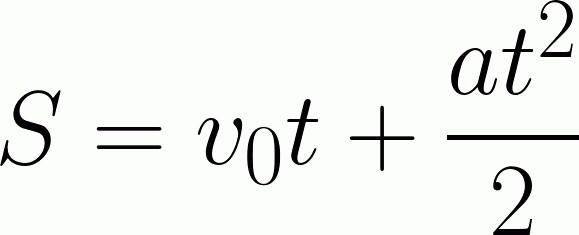
Ma qui siamo per un intoppo, di cui abbiamo parlato prima. Conoscere le formule non è sufficiente - devi essere in grado di usarle. Ovvero, produci un valore usando formule alternative, trovalo e sostituiscilo. Quando si visualizzano le informazioni iniziali disponibili nell'attività, diventa immediatamente chiaro che per risolverlo semplicemente non funzionerà. Nulla viene detto sull'accelerazione, ma ci sono informazioni su come la velocità è cambiata in un certo periodo di tempo. Quindi possiamo trovare l'accelerazione da soli. Prendi la formula per trovare la velocità istantanea. Lei ha uno sguardo

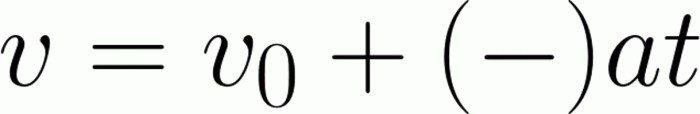
Accelerazione e tempo sono lasciati in una parte e la velocità iniziale viene trasferita all'altra. Quindi dividendo entrambe le parti per un po 'rilasciamo il lato destro. Qui puoi calcolare immediatamente l'accelerazione, sostituendo i dati diretti. Ma è molto più opportuno esprimere ulteriormente. La formula ottenuta per l'accelerazione è sostituita nella principale. Qui puoi ridurre leggermente le variabili: nel numeratore, il tempo è indicato nel quadrato e nel denominatore - nel primo grado. Pertanto, da questo denominatore puoi liberarti di. Bene, allora - una semplice sostituzione, poiché non c'è altro da esprimere. La risposta dovrebbe essere la seguente: 440 chilometri. La risposta sarà diversa se traduci i valori in un'altra dimensione.

conclusione

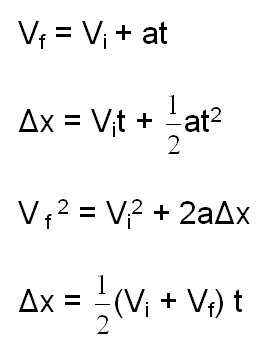
Allora, cosa abbiamo scoperto nel corso di questo articolo?

1) Il punto materiale è un corpo le cui dimensioni possono essere trascurate rispetto alle dimensioni del sistema di riferimento.

2) Per risolvere i problemi associati a un punto materiale, ci sono diverse formule (fornite nell'articolo).

3) Il segno di accelerazione in queste formule dipende dal parametro del movimento del corpo (accelerazione o decelerazione).