Sistemi numerici: esempi. Traduzione di sistemi numerici

Parlando nel linguaggio più semplice, il sistema numerico è un modo di rappresentare i numeri. Abbiamo usato il metodo di calcolo durante il calcolo 10. Altri sistemi numerici, ad esempio, hanno una base di 16 (esadecimale), 8 (ottale) e 2 (binario).

Tempi preistorici

Proprio come i primi tentativi di scrivere sono apparsi dopo lo sviluppo del discorso, i primi tentativi di rappresentare graficamente i numeri sono apparsi dopo che le persone hanno imparato a contare. Probabilmente il primo modo per contare è una sorta di sistema per contare oggetti fisici, come ciottoli o bastoncini. A giudicare dai costumi degli attuali popoli indigeni, oltre alle più antiche tracce di reperti scritti o scultorei, le prime figure erano semplici tagli su tavole, graffi su una pietra, segni su un pezzo di ceramica, ecc. Senza avere unità fisse, niente monete, niente scambi oltre al baratto più primitivo, al sistema di tassazione e ai bisogni diversi da quelli che sostenevano la vita, la gente non aveva bisogno di numeri scritti fino all'inizio dei cosiddetti periodi storici.

I primi metodi di conteggio

Quando è stato necessario contare spesso cifre superiori a 10, la numerazione doveva essere sistematizzata e semplificata; questo di solito veniva fatto usando una base di gruppo o di gruppo. Infatti, i primi numeri registrati erano semplici segni lineari per piccoli numeri con una forma speciale per 10. Questi simboli apparvero in Egitto già nel 3400 aC e in Mesopotamia già nel 3000 aC, a Creta (circa 1200 aC D.C.) e in India (circa 300 aC).

Ovviamente, un posto speciale è occupato dal numero 10 del numero di dita umane, e ciò conferma l'uso corrente di questo quadro, non solo nella struttura logica del sistema decimale, ma anche nei nomi dei numeri in molte lingue.

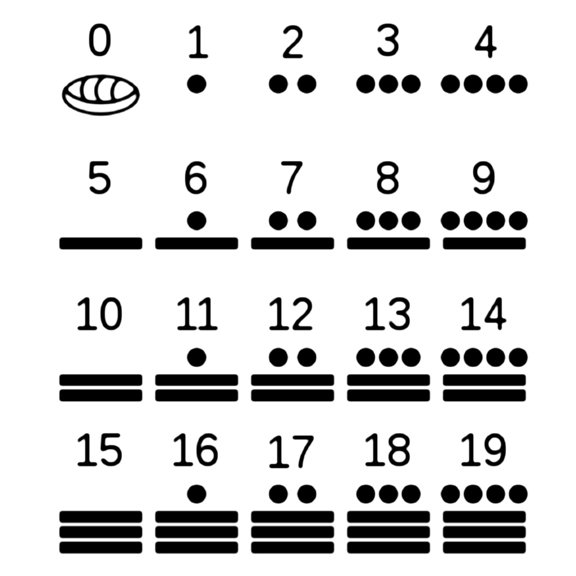
Varietà di metodi di conteggio

Tuttavia, non si dovrebbe concludere che 10 sia l'unica base possibile o l'unica effettivamente utilizzata. Ci sono molti esempi di sistemi numerici. Binario, in cui il conteggio è "uno, due, due e uno, due e due, due e due e uno", ecc., Si trova tra le più antiche tribù dell'Australia, in molte lingue dei popoli dello Stretto di Torres e della costa adiacente della Nuova Guinea, tra alcuni pigmei africani e varie tribù sudamericane. Le popolazioni indigene della Terra del Fuoco e del continente sudamericano utilizzano i sistemi numerici con le basi tre e quattro. Il sistema di base numero cinque è molto antico, ma nella sua forma pura, sembra essere usato attualmente solo in alcune tribù del Sud America. In altri luoghi, è combinato con un sistema decimale o decimale, dove la base è 20. Analogamente, un sistema basato su 6 è raro nell'Africa nordoccidentale ed è associato a un sistema di base duodenale 12.

Nel corso dello sviluppo storico, il sistema decimale alla fine ha messo in ombra tutti gli altri. Tuttavia, ci sono ancora molti altri sistemi che vengono utilizzati principalmente nelle industrie commerciali e residenziali. Quindi, la base 12 si presenta come un numero di pollici in piedi, mesi in un anno, once in una libbra, e due volte per 12 ore al giorno, così come una dozzina usata nel calcolo. La base 60 si trova quando si misurano il tempo e gli angoli.

Sistemi digitali

Le prime cifre primitive erano |, ||, ||| ecc., ad esempio, in Egitto e nell'antica Grecia, o -, = ,, ecc., come in Asia orientale. Questo metodo di calcolo corrispondeva ai semplici bisogni delle persone. Man mano che la vita diventava più complessa, la necessità del numero di gruppi di numeri diventava ovvia, ed era solo un piccolo passo da un semplice sistema con i nomi per solo uno e dieci alla comparsa di altri numeri speciali, in base ai quali è possibile determinare quanti sistemi numerici esistevano ed esistono. A volte questo processo non era sistematico. Ad esempio, lo Yukaghir della Siberia considera "uno, due, tre, tre e uno, cinque, due tre, due tre e uno, due quattro, dieci con uno mancato, dieci". Solitamente, tuttavia, un sistema più regolare ha portato al fatto che la maggior parte di questi sistemi può essere classificata, almeno in termini generali, secondo i principi logici sottostanti.

Semplici sistemi di raggruppamento

In base al suo valore, il sistema numerico può essere considerato un metodo per raggruppare i numeri. Nella sua forma pura, un semplice sistema di raggruppamento è l'assegnazione di nomi speciali per numeri piccoli, la base b e i suoi poteri b2, b3, ecc., Ad un grado sufficiente per rappresentare tutti i numeri realmente necessari per l'uso. I numeri intermedi vengono quindi formati aggiungendo, ogni carattere viene ripetuto il numero richiesto di volte, proprio come 23 è scritto - XXIII - in numeri romani.

Il primo esempio di questo tipo di sistema numerico è un modello trovato nei geroglifici egizi. Era usato dagli antichi egizi per scrivere sulla pietra.

Sistemi numerici posizionali

Questi includono quelli in cui la posizione (cifra) quando si scrive un numero determina il suo valore. Il sistema dei numeri decimali è un esempio di un sistema posizionale in cui, dopo che la base b è stata adottata, i nomi speciali sono assegnati ai numeri 1, 2, ..., b-1 e tutti i numeri più grandi sono scritti come sequenze di queste figure. È l'unico tra i vari sistemi numerici che può essere utilizzato per descrivere grandi numeri. Questo perché ciascuno degli altri tipi dà nomi speciali a numeri diversi maggiori di b, e tutti i numeri richiedono un numero infinito di nomi. Il successo del sistema di numeri posizionali dipende dal fatto che per una base arbitraria b ogni numero N può essere scritto in modo univoco nella forma:

N = anbn + an - 1bn - 1 + ⋯ + a1b + a0,

dove a, an - 1, ..., a0 sono numeri; cioè, i numeri dal gruppo 0, 1, ..., b - 1. Quindi N alla base b può essere rappresentato da una sequenza di anan - 1 ... a1a0 caratteri. Questo principio è stato utilizzato nei sistemi di raggruppamento moltiplicativi. Il sistema posizionale deriva dal moltiplicativo semplicemente escludendo i nomi dei gradi b, b2, ecc. Ed è determinato in base alla posizione dei numeri per la presentazione di questa informazione. Tuttavia, allora è necessario usare un carattere per zero per indicare qualsiasi autorità di base mancante; altrimenti, 792 può significare, ad esempio, 7M9X2 (ovvero 7.092) o 7C9X2 (792).

Sviluppo in diversi paesi

Un esempio di questo tipo di sistema numerico è il metodo sviluppato dai babilonesi (circa 3000-2000 aC). Qui, come base è stato usato il numero 60. Tale sistema è chiamato esadecimale. Con una base così ampia, sarebbe scomodo avere nomi non correlati per i numeri 0, 1, ..., 59, quindi per questi numeri è stato utilizzato un semplice sistema di raggruppamento sul fondo 10.

Oltre al fatto che questo sistema era ingombrante a causa della sua ampia base, il sistema babilonese soffrì fino a molto tardi dall'assenza di un marchio di zero.

Durante le prime spedizioni nello Yucatan, fu scoperto un altro esempio del sistema di numeri Maya. Era usato principalmente nel calendario, non per calcoli commerciali o di altro tipo. Era un sistema posizionale ben sviluppato. La sua base era il numero 20. I numeri 0, 1, ..., 19, come in Babylon, sono formati da un semplice sistema di raggruppamento, in questo caso alla base 5.

Né il sistema Maya né quello babilonese sono ideali per i calcoli aritmetici, perché le figure inferiori a 20 o 60 non erano rappresentate da singoli caratteri.

evoluzione

Ulteriore sviluppo di questa idea è connesso con gli indiani, che furono anche i primi a usare zero nell'immagine moderna. Nei sistemi di posizionamento, è necessario del carattere per contrassegnare un luogo in cui la base non è effettivamente trovata. Gli indù lo indicavano con un punto o un piccolo cerchio, a cui era stato dato il nome sunya, la parola sanscrita "vuoto". Quindi, circa 800 d.C. questa designazione fu passata agli arabi, e in traduzione il valore fu mantenuto invariato. Successivamente, è stato introdotto nella lingua latina (circa 1200), mentre la pronuncia è stata conservata, ma il valore è stato ignorato. I successivi cambiamenti hanno portato alla designazione moderna.

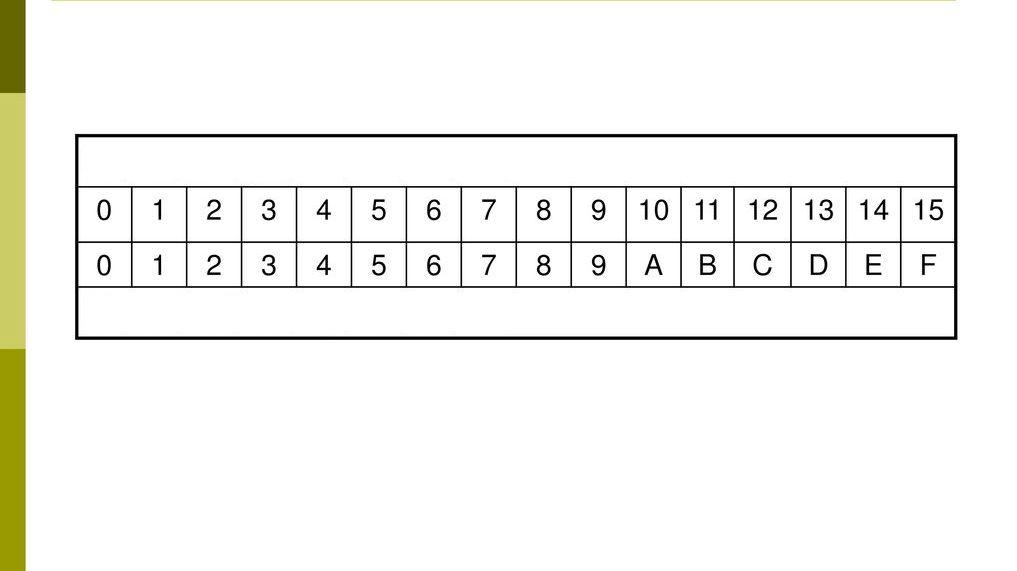
Sistema arabo-indù

Ci sono diverse opinioni riguardo all'origine dei numeri occidentali moderni: di solito parlano della loro origine araba, ma è preferibile considerare l'arabo indù. In questo caso, si sostiene che la loro origine sia associata agli arabi, ai persiani, agli egiziani e agli indù. Non è escluso che la comunicazione tra mercanti sia servita come un'opportunità per trasferire questi simboli da un paese all'altro, in modo che le figure occidentali moderne possano provenire da varie fonti. Tuttavia, per quanto è noto, il paese che per primo ha utilizzato il maggior numero di queste forme numeriche è l'India. 1, 4 e 6 si trovano nelle iscrizioni di Ashoka (III secolo aC); 2, 4, 6, 7 e 9 compaiono nelle iscrizioni di Nana Ghat dopo circa un secolo; e 2, 3, 4, 5, 6, 7 e 9 nelle caverne di Nasik I o II secolo d.C. Tutti questi numeri avevano una forma in gran parte simile a quella di oggi.

I vantaggi che un sistema di posizionamento perfetto possiede sono così numerosi e così ovvi che i numeri indù-arabi e la base 10 sono stati accettati quasi ovunque. Si può dire che questo è l'approccio più vicino al linguaggio umano universale.

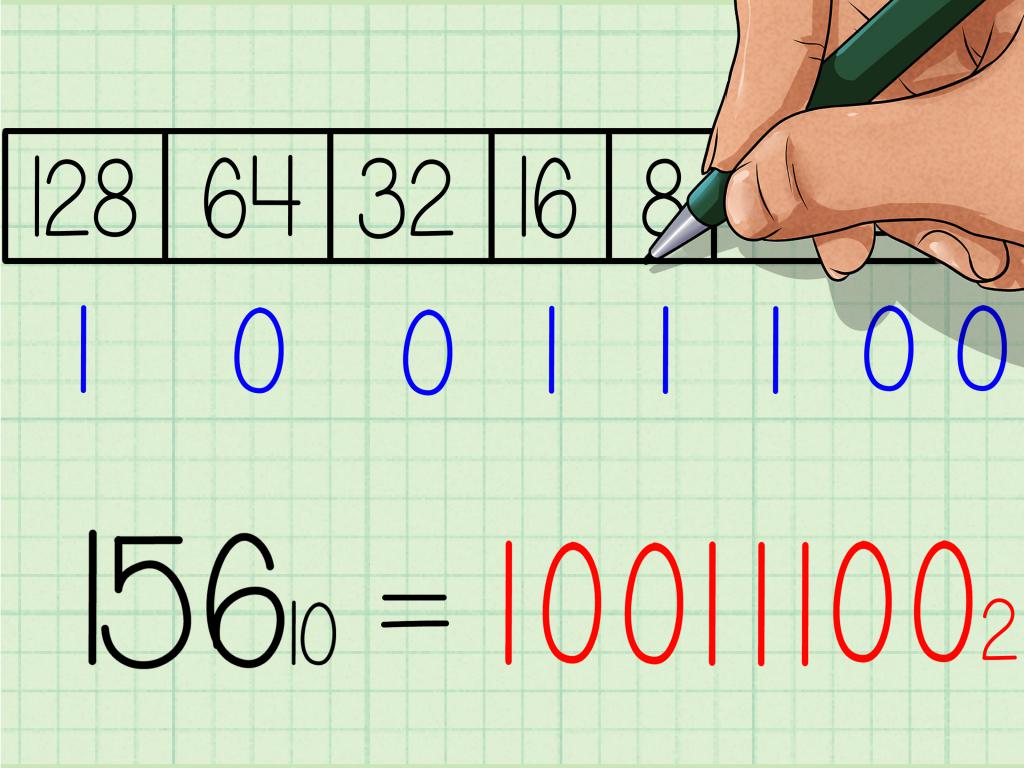
Sistema binario

Tuttavia, esiste un'area in cui il solito sistema decimale non è il migliore: il computer. Qui il sistema posizionale binario ha più vantaggi rispetto al decimale. In questo sistema, la base 2 determina quanti numeri ci sono nel sistema di numeri binari: qui ci sono solo due cifre: 0 e 1; il numero due è rappresentato qui come 10, poiché ha lo stesso ruolo di dieci nel sistema decimale.

Un numero binario di solito è molto più lungo del suo numero decimale corrispondente; ad esempio, 256 058 ha una rappresentazione binaria 111 11010 00001 11010. Una cifra binaria, come un'unità nel sistema numerico, trasporta meno informazioni di una cifra decimale. La ragione per la maggiore lunghezza di un numero binario è che una cifra binaria distingue solo due possibilità: 0 o 1, mentre una cifra decimale distingue tra 10 possibilità.

Sistemi numerici ottali ed esadecimali

Il loro uso è anche associato a computer e programmazione.

Il vecchio sistema di numerazione computer è il numero ottale, dove la base è il numero 8. I numeri utilizzati in questo sistema sono: 0, 1, 2, 3, 4, 5, 6 e 7. Il valore "otto" è registrato come "1 otto e 0 unità" o 10. Ogni valore di posizione è otto volte diverso dal successivo.

Da un punto di vista tecnico, ci sono tanti protocolli linguistici per il sistema ottale.

L'altro sistema è denominato esadecimale, poiché questo sistema ha una base di 16. I codici validi includono i normali caratteri decimali 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9, nonché sei caratteri alfabetici A, B, C , D, E e F, per un totale di sedici. Il valore di ciascuna posizione differisce da quello precedente sedici volte.

I sistemi ottali ed esadecimali sarebbero privi di significato se non fosse per la loro capacità di essere facilmente convertiti da e verso il sistema binario. Il loro obiettivo principale è quello di servire come un metodo "abbreviato" per designare un numero rappresentato elettronicamente in forma binaria. Poiché le basi dei sistemi ottale (8) ed esadecimale (16) sono pari e multipli della base binaria (2), i bit binari possono essere raggruppati e i numeri nei sistemi numerici possono essere convertiti direttamente in cifre ottali o esadecimali. Quando si converte nel sistema ottale, i bit binari sono raggruppati in tre (perché 23 = 8), e in esadecimale - i bit binari sono raggruppati in quattro (perché 24 = 16).

Analogamente, la conversione dei numeri in numeri ottali o esadecimali in numeri binari viene eseguita utilizzando ogni cifra ottale o esadecimale e convertendola in un gruppo binario equivalente (3 o 4 bit), quindi tutti i gruppi di bit vengono combinati.