Volume parallelepipedo: formule di base ed esempi di attività
Spesso gli studenti chiedono indignati: "Come posso usarlo nella vita?" Su qualsiasi argomento di ogni argomento Il problema del volume parallelepiped non fa eccezione. E qui puoi solo dire: "È utile".
Come, ad esempio, scoprire se il pacchetto si adatta alla casella di posta? Naturalmente, è possibile, per tentativi ed errori, scegliere quello appropriato. E se non esiste tale possibilità? Quindi i calcoli verranno in soccorso. Conoscendo la capacità della scatola, è possibile calcolare il volume del pacchetto (almeno approssimativamente) e rispondere alla domanda posta.
Parallelepipedo e suoi tipi
Se traduci letteralmente il suo nome dal greco antico, si scopre che questa è una figura composta da piani paralleli. Esistono definizioni equivalenti di un parallelepipedo:
Ad
- prisma con una base sotto forma di un parallelogramma;
- poliedro, ogni faccia della quale è un parallelogramma.
I suoi tipi si distinguono a seconda di quale figura si trova alla base e di come sono diretti i bordi laterali. In generale, parlano di un parallelepipedo inclinato , la cui base e tutte le facce sono parallelogrammi. Se, nella vista precedente, le facce laterali diventano rettangoli, sarà necessario chiamarle linee rette . E la base rettangolare ha anche angoli di 90º.
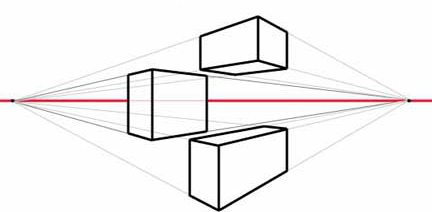
E i secondi in geometria stanno cercando di ritrarre in modo che sia evidente che tutti i bordi sono paralleli. Qui, tra l'altro, si osserva la principale differenza tra matematici e artisti. Infine, è importante trasferire il corpo nel rispetto della legge della prospettiva. E in questo caso il parallelismo delle costole è completamente invisibile.
Ad
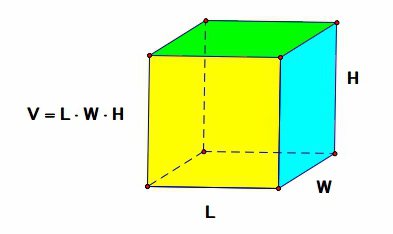
Informazioni sulla notazione inserita
Nelle formule seguenti, la notazione nella tabella è valida.
| valore | La sua designazione |
| lunghezze del bordo di base | e, in |
| lunghezza della costola laterale | con |
| l'altezza | n |
| area di base | S o |
| superficie laterale | S b |
| superficie totale | S p |
| perimetro di base | R o |
| volume | V |
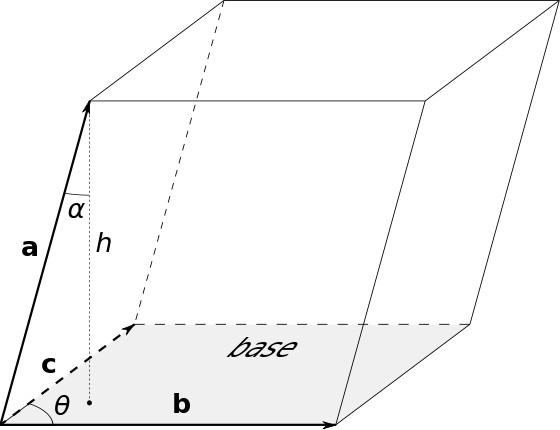
Formule per parallelepipedo obliquo
Il primo e il secondo per lo spazio:
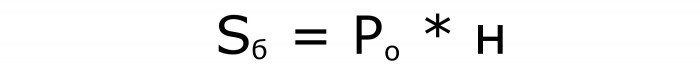
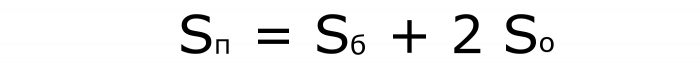
Il terzo per calcolare il volume del parallelepipedo:

Poiché la base è un parallelogramma, quindi per calcolare la sua area, sarà necessario utilizzare le espressioni appropriate.
Formule per parallelepipedo rettangolare
Simile al primo elemento: due formule per le aree:
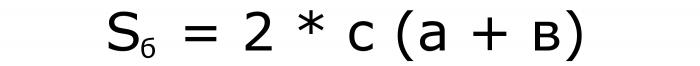
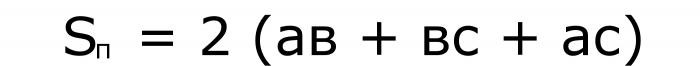
E uno di più per il volume:

Primo compito
Condizioni. Dato un parallelepipedo rettangolare, il volume di cui si desidera trovare. Diagonale nota - 18 cm - e il fatto che forma angoli di 30 e 45 gradi con il piano della faccia laterale e del bordo laterale, rispettivamente.
La decisione Per rispondere alla domanda del problema, è necessario conoscere tutte le parti in tre triangoli rettangoli. Daranno i valori necessari dei bordi, che devono essere contati del volume.
Per prima cosa devi scoprire dove si trova l'angolo a 30 °. Per fare ciò, è necessario disegnare una diagonale della faccia laterale dallo stesso vertice da cui è stata disegnata la diagonale principale del parallelogramma. L'angolo tra loro sarà ciò che è necessario.
Il primo triangolo, che darà uno dei valori dei lati della base, sarà il prossimo. Contiene il lato desiderato e due in diagonale. È rettangolare Ora è necessario utilizzare il rapporto tra il lato opposto (lato base) e ipotenusa (diagonale). È uguale al seno di 30º. Cioè, il lato sconosciuto della base sarà definito come una diagonale moltiplicata per il seno di 30º o ½. Lascia che sia contrassegnato con la lettera "a".
Ad
È facile contare: a = 18 * ½ = 9 (cm).
Il secondo sarà un triangolo contenente una diagonale conosciuta e un bordo con cui si forma a 45º. È anche rettangolare, e puoi ancora usare la relazione della gamba con l'ipotenusa. In altre parole, il bordo laterale della diagonale. È uguale al coseno di 45º. Cioè, "c" è calcolato come il prodotto della diagonale dal coseno di 45º.
c = 18 * 1 / √2 = 9 √2 (cm).
Nello stesso triangolo è richiesto per trovare un'altra gamba. Questo è necessario per poi contare il terzo sconosciuto - "in". Lascia che sia contrassegnato con la lettera "x". È facile da calcolare con il teorema di Pitagora:
x = √ (18 2 - (9√2) 2 ) = 9√2 (cm).
Ora dobbiamo considerare un altro triangolo rettangolo. Contiene i lati già conosciuti "s", "x" e quello che devi contare, "c":
c = √ ((9√2) 2 - 9 2 = 9 (cm).
Tutte e tre le quantità sono note. Puoi usare la formula per il volume e contarli:
V = 9 * 9 * 9√2 = 729√2 (cm 3 ).
Risposta: il volume del parallelepipedo è 729√2 cm 3 .
Secondo compito
Condizioni. È necessario trovare il volume del parallelepipedo. Sono noti i lati del parallelogramma, che si trova alla base, 3 e 6 cm, così come il suo angolo acuto - 45º. Il bordo laterale ha una pendenza alla base di 30º ed è di 4 cm.
Ad
La decisione Per rispondere alla domanda del problema, è necessario prendere la formula che è stata scritta per il volume del parallelepipedo inclinato. Ma entrambe le quantità sono sconosciute.
L'area della base, cioè il parallelogramma, sarà determinata dalla formula in cui è necessario moltiplicare i lati conosciuti e il seno dell'angolo acuto tra di loro.
S о = 3 * 6 sin 45º = 18 * (√2) / 2 = 9 √2 (cm 2 ).
Il secondo sconosciuto è altezza. Può essere disegnato da uno qualsiasi dei quattro vertici sopra la base. Può essere trovato da un triangolo rettangolo, in cui l'altezza è la gamba e il bordo laterale è l'ipotenusa. L'angolo di 30º si trova di fronte all'altezza sconosciuta. Quindi, puoi usare l'atteggiamento della gamba sull'ipotenusa.
n = 4 * sin 30º = 4 * 1/2 = 2.
Ora tutti i valori sono noti e puoi calcolare il volume:
V = 9 √2 * 2 = 18 √2 (cm 3 ).
Risposta: il volume è 18 √2 cm 3 .
Terzo compito
Condizioni. Trova il volume del parallelepipedo, se sai che è dritto. I lati della sua base formano un parallelogramma e sono 2 e 3 cm L'angolo acuto tra loro è di 60º. La diagonale più piccola del parallelepipedo è uguale alla diagonale più grande della base.
La decisione Per scoprire il volume del parallelepipedo, usiamo la formula con l'area di base e l'altezza. Entrambe le quantità sono sconosciute, ma non sono difficili da calcolare. Il primo è l'altezza.
Poiché la diagonale più piccola del parallelepipedo coincide in dimensione con base più ampia, possono essere designati con una lettera d. L'angolo maggiore del parallelogramma è 120º, poiché si forma a 180º con uno appuntito. Lascia che la seconda diagonale della base sia contrassegnata con la lettera "x". Ora per le due diagonali di base si può scrivere teoremi di coseno :
Ad
d 2 = a 2 + in 2 - 2av cos 120º,
x 2 = a 2 + in 2 - 2av cos 60º.
Trovare valori senza quadrati non ha senso, da allora saranno di nuovo elevati alla seconda potenza. Dopo aver ottenuto la sostituzione dei dati:
d 2 = 2 2 + 3 2 - 2 * 2 * 3 cos 120º = 4 + 9 + 12 * ½ = 19,
x 2 = a 2 + in 2 - 2av cos 60º = 4 + 9 - 12 * ½ = 7.
Ora l'altezza, che è il bordo laterale del parallelepipedo, sarà la gamba nel triangolo. L'ipotenusa sarà la nota diagonale del corpo e la seconda sarà la "x". Puoi scrivere il teorema di Pitagora:
n 2 = d 2 - x 2 = 19 - 7 = 12.
Da qui: n = √12 = 2√3 (cm).
Ora la seconda quantità sconosciuta è l'area della base. Può essere contato con la formula menzionata nel secondo problema.
S о = 2 * 3 sin 60º = 6 * √3 / 2 = 3√3 (cm 2 ).
Combinando tutto nella formula del volume, otteniamo:
V = 3√3 * 2√3 = 18 (cm 3 ).
Risposta: V = 18 cm 3 .

Quarto compito
Condizioni. È necessario conoscere il volume del parallelepipedo che soddisfa queste condizioni: base - un quadrato con un lato di 5 cm; le facce laterali sono rombi; uno dei vertici sopra la base è equidistante da tutti i vertici alla base.
La decisione Per prima cosa devi affrontare la condizione. Con il primo paragrafo sulla piazza non ci sono domande. Il secondo, sui rombi, chiarisce che il parallelepipedo è inclinato. Inoltre, tutti i suoi bordi sono 5 cm, poiché i lati del rombo sono gli stessi. E dal terzo risulta chiaro che le tre diagonali che ne derivano sono uguali. Questi sono due che si trovano sulle facce laterali, e l'ultimo è all'interno del parallelepipedo. E queste diagonali sono uguali al bordo, cioè hanno anche una lunghezza di 5 cm.
Per determinare il volume, sarà necessaria una formula scritta per un parallelepipedo inclinato. Di nuovo, non ci sono valori noti. Tuttavia, l'area della base è facile da calcolare perché è quadrata.
S o = 5 2 = 25 (cm 2 ).
Un po 'più difficile è il caso dell'altezza. Sarà tale in tre figure: un parallelepipedo, una piramide quadrangolare e un triangolo isoscele. L'ultima circostanza e necessità di approfittare.
Dal momento che è altezza, è una gamba in un triangolo rettangolo. L'ipotenusa in esso sarà un bordo noto, e la seconda gamba è uguale alla metà della diagonale del quadrato (l'altezza è anche la mediana). E la diagonale della base è facile da trovare:
d = √ (2 * 5 2 ) = 5√2 (cm).
Sarà necessario contare l'altezza come differenza del secondo grado del bordo e il quadrato della metà della diagonale e ricordare di estrarre radice quadrata :
n = √ (5 2 - (5/2 * √2) 2 ) = √ (25 - 25/2) = √ (25/2) = 2,5 √2 (cm).
Resta da contare il volume:
V = 25 * 2,5 √2 = 62,5 √2 (cm 3 ).
Risposta: 62,5 √2 (cm 3 ).