Altezza della piramide: definizione, formule, calcoli

Una delle figure volumetriche studiate nel corso della geometria spaziale è la piramide. Una caratteristica importante di questa figura è la sua altezza. Nell'articolo daremo una definizione dell'altezza della piramide e forniremo le formule attraverso le quali è collegata ad altre caratteristiche lineari.

Cos'è una piramide

Sotto la piramide comprendi la forma geometrica dello spazio, che si ottiene collegando tutti gli angoli del poligono con un punto nello spazio. La figura seguente mostra la disposizione delle linee (bordi) per le piramidi quadrangolari e pentagonali.

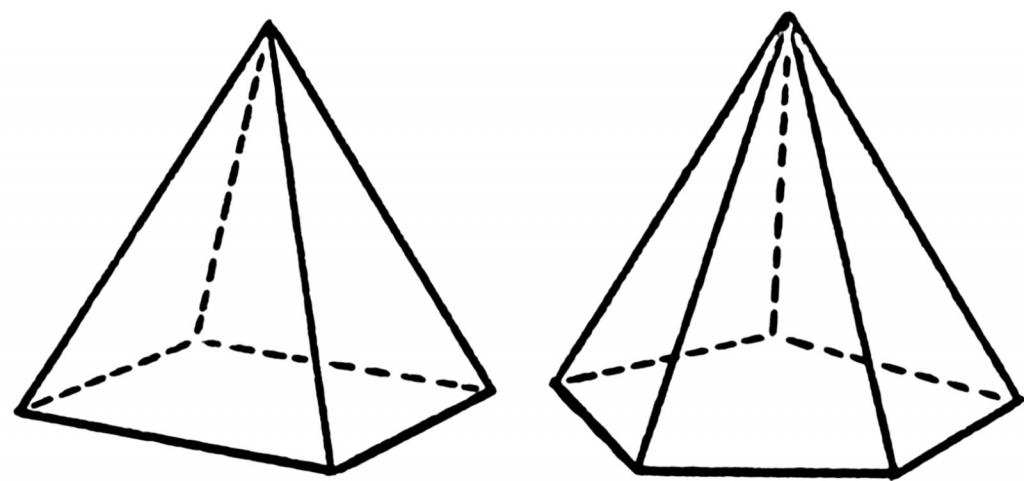
La faccia poligonale della forma è chiamata la sua base. Il punto in cui tutte le facce triangolari si connettono è chiamato vertice. Per determinare l'altezza della piramide, gli elementi contrassegnati sono importanti.

Altezza del corpo

L'altezza della piramide è chiamata perpendicolare, che dalla sua sommità si abbassa sul piano della base. È importante capire che da ciascun vertice appartenente alla base della figura, è anche possibile disegnare una perpendicolare alla corrispondente faccia triangolare, ma non apparirà così alta. L'altezza della piramide è l'unica perpendicolare che è una delle sue importanti caratteristiche lineari.

Ogni scolaro sa che qualsiasi figura piatta possiede un centro geometrico (in fisica, corrisponde al centro di massa). Ad esempio, il centro geometrico per un triangolo arbitrario è determinato dal punto di intersezione delle sue mediane, per un parallelogramma, il punto di intersezione delle diagonali. Se l'altezza della piramide interseca la sua base nel centro geometrico, la figura viene chiamata linea retta. La piramide è dritta, con un poligono di base con gli stessi lati e angoli, chiamato quello corretto.

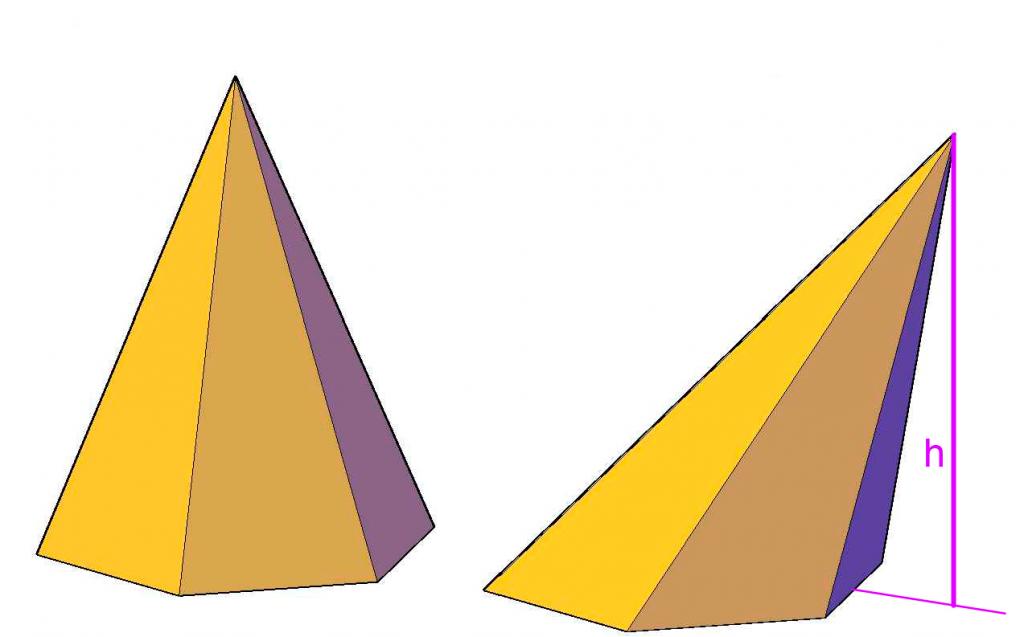
La figura sopra mostra la differenza tra la piramide sbagliata e quella corretta. Si può vedere che l'altezza della forma irregolare si trova oltre la sua base, mentre in una piramide esagonale regolare l'altezza è all'interno della forma, intersecando la sua base nel centro geometrico.

Le proprietà importanti di tutte le piramidi regolari sono le seguenti:

• tutte le facce laterali sono triangoli isosceli e sono uguali tra loro;
• le lunghezze delle costole laterali e l'apotema sono le stesse.

Formule per l'altezza di una piramide regolare

Ci sono quattro caratteristiche lineari di base per qualsiasi piramide corretta:

• lato della base;
• bordo laterale;
• apotema del lato laterale;
• altezza della figura.

Tutti loro sono matematicamente correlati l'uno all'altro. Indichiamo la lunghezza del lato della base di a, un'altezza - h, apotem - h _b e bordo - b. Le formule che legano queste quantità hanno un aspetto individuale per la corrispondente piramide di carbone n. Ad esempio, per una piramide regolare, l'altezza quadrangolare può essere determinata dalle formule:

h = √ (a _b ² - a 2/4);

h = √ (b ² - a 2/2).

Queste formule derivano dal teorema di Pitagora quando si considerano i corrispondenti triangoli rettangoli all'interno della piramide.

Se viene considerata una figura con una base triangolare, le seguenti formule sono valide per l'altezza di una piramide regolare:

h = √ (a _b ² - a 2/12);

h = √ (b ² - a 2/3).

Soluzione del problema con una piramide esagonale

Supponiamo di avere una piramide regolare con una base esagonale. È noto che l'altezza della base della piramide è di 13 cm. Sapendo che la lunghezza del suo bordo laterale è di 10 cm, è necessario calcolare il volume e l'altezza di una normale piramide esagonale.

La figura seguente mostra come appare un esagono regolare.

La distanza tra uno dei suoi due lati paralleli è detta altezza. Non è difficile dimostrare che questa altezza ha è correlata alla lunghezza del lato della figura con la seguente formula:

h _a = a * √3

Sostituendo il valore di h _a nell'espressione, troviamo che il lato di base di a è pari a 7,51 cm.

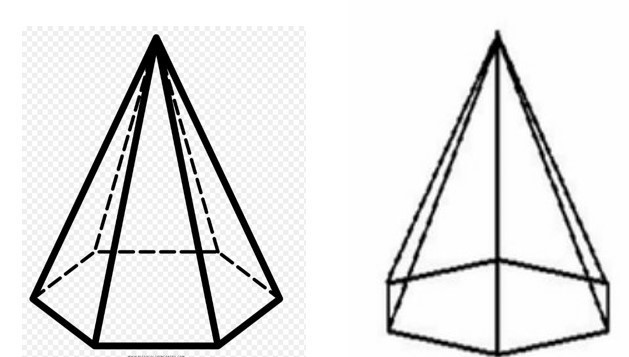
L'altezza h della figura può essere determinata considerando un triangolo rettangolo all'interno della piramide e costituito da due gambe (l'altezza della piramide e metà della diagonale della base esagonale) e l'ipotenusa (bordo laterale). Quindi il valore di h sarà uguale a:

h = √ (b ² - a ² ) = √ (100 - 56,3) = 6,6 cm.

Il volume della piramide è definito come la terza parte del prodotto dell'altezza della figura sull'area della sua base. L'area di un esagono regolare è:

S ₆ = n / 4 * a ² * ctg (pi / n) = 6/4 * a ² * ctg (pi / 6) = 3 * √ 3/2 * a ² = 3 * √ 3/2 * 56, 4 ≈ 146,53 cm ² .

La formula utilizzata per calcolare S ₆ è universale per un arbitrario regolare n-gon.

Per determinare il volume della figura, rimane da sostituire i parametri trovati nella formula appropriata:

V = 1/3 * h * S ₆ = 1/3 * 6.6 * 146.53 = 322.366 cm ³ .

Abbiamo ottenuto il valore dell'altezza della piramide e calcolato il suo volume. Quindi, il problema è risolto.