Movimento rotazionale del corpo. Legge del moto rotatorio
Questo articolo descrive una sezione importante della fisica - "Cinematica e dinamica del movimento rotazionale".
Concetti di base della cinematica del moto rotatorio
Movimento di rotazione punto materiale attorno a un asse fisso si parla di un tale movimento, la cui traiettoria è un cerchio situato nel piano perpendicolare all'asse, e il suo centro giace sull'asse di rotazione.
Il movimento rotatorio di un corpo solido è un movimento in cui tutti i punti del corpo si muovono lungo cerchi concentrici (i cui centri si trovano sullo stesso asse) in conformità con la regola del movimento rotatorio di un punto materiale.
Lasciare un corpo rigido arbitrario T ruotare attorno all'asse O, che è perpendicolare al piano della figura. Scegli il punto M su questo corpo: durante la rotazione, questo punto descriverà un cerchio con raggio r attorno all'asse O.
Ad
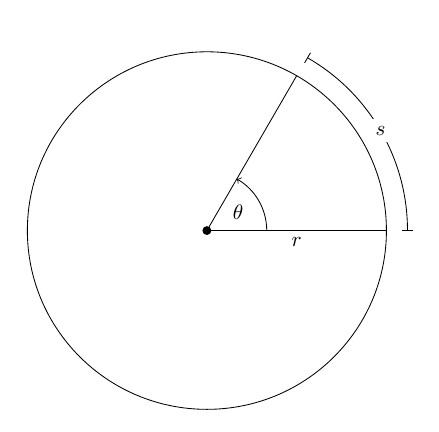
Dopo un po 'di tempo, il raggio ruoterà rispetto alla posizione iniziale di un angolo Δφ.
La direzione della vite destra (in senso orario) viene presa come direzione di rotazione positiva. Il cambiamento nell'angolo di rotazione con il tempo è chiamato l'equazione del moto rotatorio di un solido:
φ = φ (t).
Se φ è misurato in radianti (1 rad è l'angolo corrispondente ad un arco con una lunghezza pari al suo raggio), quindi la lunghezza dell'arco di un cerchio ΔS, che il punto materiale M passerà durante il tempo Δt, è uguale a:
ΔS = Δφr.
Gli elementi principali della cinematica del moto rotatorio uniforme
Una misura del movimento di un punto materiale in un breve periodo di tempo dt è il vettore di rotazione elementare dφ .
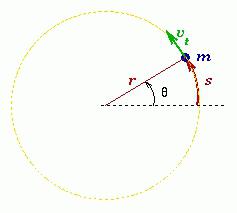
Velocità angolare il punto materiale o il corpo è una quantità fisica, che è determinata dal rapporto tra il vettore della rotazione elementare e la durata di questa rotazione. La direzione del vettore può essere determinata dalla regola della vite destra lungo l'asse O. Nella forma scalare:
Ad
ω = dφ / dt.
Se ω = dφ / dt = const, allora un tale movimento è chiamato moto rotazionale uniforme. Quando è la velocità angolare è determinata dalla formula
ω = φ / t.
Secondo la formula preliminare, la dimensione della velocità angolare
[ω] = 1 rad / s.
Il movimento rotatorio uniforme del corpo può essere descritto dal periodo di rotazione. Il periodo di rotazione T è una quantità fisica che determina il tempo impiegato dal corpo attorno all'asse di rotazione per eseguire un giro completo ([T] = 1 s). Se nella formula per la velocità angolare prendiamo t = T, φ = 2 π (completo di un giro di raggio r), quindi
ω = 2π / T,
pertanto, il periodo di rotazione è definito come segue:
T = 2π / ω.
Il numero di giri che un corpo fa per unità di tempo è chiamato la frequenza di rotazione ν, che è uguale a:
ν = 1 / T.
Unità di frequenza: [ν] = 1 / c = 1 s -1 = 1 Hz.
Confrontando le formule per la velocità angolare e la velocità di rotazione, otteniamo un'espressione che mette in relazione queste quantità:
ω = 2πν.
Gli elementi principali della cinematica del moto rotatorio irregolare
Il movimento di rotazione irregolare di un solido o di un punto materiale attorno ad un asse fisso caratterizza la sua velocità angolare, che varia col tempo.
Il vettore ε , che caratterizza il tasso di variazione della velocità angolare, è chiamato il vettore dell'accelerazione angolare:
ε = dω / dt.
Se il corpo ruota, accelerando, cioè, dω / dt> 0 , il vettore ha una direzione lungo l'asse nella stessa direzione di ω.
Se il movimento rotatorio è lento - dω / dt <0 , allora i vettori ε e ω sono diretti opposti.
Nota. Quando si verifica un movimento rotatorio non uniforme, il vettore ω può cambiare non solo in grandezza, ma anche in direzione (quando l'asse di rotazione viene ruotato).
La relazione delle quantità che caratterizzano il movimento traslazionale e rotazionale
È noto che la lunghezza dell'arco con l'angolo di rotazione del raggio e il suo valore è correlata da
ΔS = Δφ r.
Quindi la velocità lineare del punto materiale esegue il movimento rotatorio
υ = ΔS / Δt = Δφr / Δt = ωr.
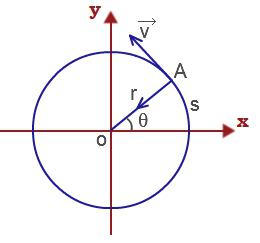
Accelerazione normale di un punto materiale che funziona a rotazione movimento in avanti definiamo come segue:
a = υ 2 / r = ω 2 r 2 / r.
Quindi, nella forma scalare
a = ω 2 r.
Punto materiale tangenziale accelerato che esegue il movimento rotatorio
a = ε r.
Momento di slancio di un punto materiale
Il vettore vettoriale del raggio vettore della traiettoria di un punto materiale di massa m per il suo momento è chiamato il momento angolare di questo punto rispetto all'asse di rotazione. La direzione del vettore può essere determinata usando la regola della vite a destra.
Ad
Il momento della quantità di moto del punto materiale ( L i ) è diretto perpendicolare al piano tracciato attraverso r i e υ i e forma con essi i tre vettori giusti (ovvero, spostandosi dalla fine del vettore r i a υ i, la vite destra mostrerà la direzione del vettore L i ).
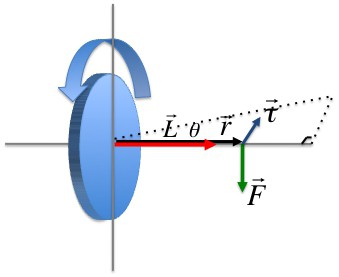
In forma scalare
L = m i υ i r sin (υ i , r i ).
Considerando che quando si muove in circolo, il vettore del raggio e il vettore di velocità lineare per il punto materiale i-esimo sono reciprocamente perpendicolari,
peccato (υ i , r i ) = 1.
Quindi il momento angolare del punto materiale per il movimento rotazionale prenderà la forma
L = m i υ i r i .
Il momento di forza che agisce sul punto materiale i-esimo
Il vettore vettoriale del raggio vettore, che è trattenuto nel punto di applicazione della forza, da questa forza è chiamato il momento di forza che agisce sul punto materiale i-esimo rispetto all'asse di rotazione.
Ad
In forma scalare
M i = r i F i sin (r i , F i ).
Supponendo che r i sinα = l i , Mi i = l i F i .
Il valore di l i uguale alla lunghezza della perpendicolare, abbassato dal punto di rotazione alla direzione della forza, è chiamato la spalla della forza F i .
Dinamica rotazionale
L'equazione della dinamica del moto rotazionale è scritta come:
M = dL / dt.
La formulazione della legge è la seguente: la velocità di cambiamento del momento angolare di un corpo, che ruota intorno ad un asse fisso, è uguale al momento risultante su questo asse di tutte le forze esterne applicate al corpo.
Momento di impulso e momento di inerzia
È noto che per il punto materiale i-esimo il momento angolare in forma scalare è dato dalla formula
L i = m i υ i r i .
Se invece di velocità lineare sostituisca la sua espressione attraverso l'angolare:
υ i = ωr i ,
quindi l'espressione per il momento angolare assume la forma
L i = m i r i 2 ω.
La quantità I i = m i r i 2 è chiamata il momento di inerzia attorno all'asse del punto materiale i-esimo di un corpo assolutamente rigido che passa attraverso il suo centro di massa. Quindi il momento angolare del punto materiale che scriviamo:
L i = I i ω.
Il momento di un impulso di un corpo assolutamente rigido è scritto come la somma dei momenti di impulso dei punti materiali che compongono questo corpo:
L = Iω.
Momento di forza e momento di inerzia
La legge del movimento rotazionale recita come segue:
M = dL / dt.
Conosciuto per presentare il momento impulso corporeo possibile attraverso il momento di inerzia:
L = Iω.
poi
M = Idω / dt.
Dato che l'accelerazione angolare è determinata dall'espressione
ε = dω / dt,
otteniamo la formula per il momento di forza rappresentato dal momento di inerzia:
M = Iε.
Nota. Il momento di forza è considerato positivo se l'accelerazione angolare di cui è provocata è maggiore di zero e viceversa.
Teorema di Steiner. Legge di aggiunta di momenti di inerzia
Se l'asse di rotazione del corpo attraverso centro di massa non passa, quindi rispetto a questo asse puoi trovare il suo momento di inerzia secondo il teorema di Steiner:
I = I 0 + ma 2 ,
dove I 0 - il momento iniziale di inerzia del corpo; m è la massa corporea; a è la distanza tra gli assi.
Se il sistema, che ruota attorno all'asse fisso, è costituito da n corpi, allora il momento di inerzia totale di questo tipo di sistema sarà uguale alla somma dei momenti che lo compongono (la legge dell'aggiunta dei momenti di inerzia).