Alcune informazioni sul cubo e su come calcolare la superficie del cubo
Il cubo è una figura fantastica. È lo stesso da tutti i lati. Qualsiasi sua faccia può diventare istantaneamente la base o il lato. E questo non cambierà nulla. E le formule per questo sono sempre facili da ricordare. E non importa ciò che è necessario trovare: il volume o l'area del cubo. In quest'ultimo caso, non c'è nemmeno bisogno di imparare qualcosa di nuovo. Basta ricordare solo la formula del quadrato quadrato.
Qual è l'area?
Questo valore è solitamente indicato dalla lettera latina S. E questo è vero per le materie scolastiche, come la fisica e la matematica. Si misura in unità quadrate di lunghezza. Tutto dipende dai dati nei valori del problema. Questi possono essere mm, cm, m o km quadrati. E ci sono casi in cui le unità non sono nemmeno indicate. È semplicemente un'espressione numerica dell'area senza il nome.
Ad
Allora, qual è l'area? Questa è una quantità che è una caratteristica numerica della figura o del corpo del volume in questione. Mostra la dimensione della sua superficie, che è limitata dai lati della figura.
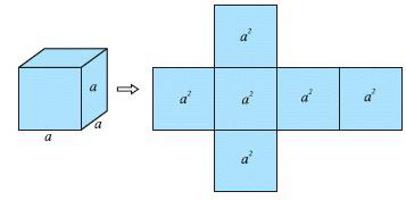
Quale forma è chiamata un cubo?
Questa figura è un poliedro. E non facile. Ha ragione, cioè ha tutti gli elementi uguali tra loro. Che si tratti di lati o bordi. Ogni superficie del cubo è un quadrato.
Un altro nome per un cubo è un esaedro regolare, se in russo, quindi un esagono. Può essere formato da un prisma quadrangolare o parallelepipedo. Soggetto alle condizioni quando tutti i bordi sono uguali e gli angoli formano 90 gradi.
Questa figura è così armoniosa che viene spesso utilizzata nella vita di tutti i giorni. Ad esempio, i primi giocattoli del bambino sono cubi. E il divertimento per chi è più vecchio è il Cubo di Rubik.

In che modo il cubo è connesso ad altre forme e corpi?
Se si disegna una sezione di un cubo che passa attraverso le sue tre facce, avrà tipo di triangolo. All'aumentare della distanza dal vertice, la sezione aumenterà. Verrà il momento in cui 4 facce si intersecheranno e la figura nella sezione diventerà un quadrilatero. Se si tiene una sezione attraverso il centro del cubo in modo che sia perpendicolare alle sue diagonali principali, si ottiene esagono regolare.
Ad
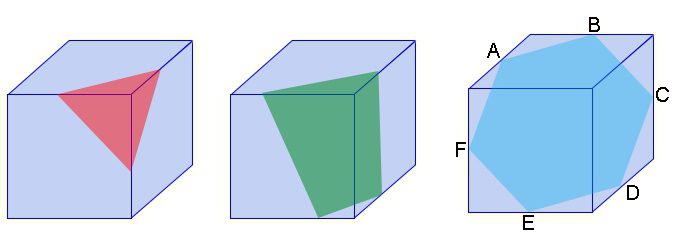
All'interno del cubo puoi disegnare un tetraedro (piramide triangolare). Per la cima del tetraedro viene preso uno dei suoi angoli. I restanti tre coincidono con i vertici che si trovano alle estremità opposte dei bordi dell'angolo selezionato del cubo.
Puoi iscriverti un ottaedro (un poliedro regolare convesso che assomiglia a due piramidi collegate). Per fare ciò, trova i centri di tutte le facce del cubo. Saranno i vertici dell'ottaedro.
È anche possibile l'operazione inversa, cioè all'interno dell'ottaedro è davvero possibile inserire un cubo. Solo ora i centri delle facce del primo diventeranno i vertici del secondo.
Metodo 1: Calcola l'area di un cubo dal suo bordo
Per calcolare l'intera superficie di un cubo, è richiesta la conoscenza di uno dei suoi elementi. Il modo più semplice per risolvere è quando il suo vantaggio è noto o, in altre parole, il lato del quadrato di cui è composto. Di solito questo valore è indicato dalla lettera latina "a".
Ora dobbiamo ricordare la formula con cui viene calcolato il quadrato. Per non confondersi, la sua designazione è introdotta dalla lettera S 1 .
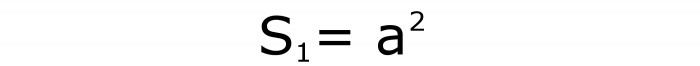
Per comodità, è meglio assegnare numeri a tutte le formule. Questo sarà il primo.
Ma questo è solo un quadrato. Ce ne sono sei: 4 sui lati e 2 sul fondo e sulla parte superiore. Quindi la superficie del cubo viene calcolata con la seguente formula: S = 6 * a 2 . Il suo numero è 2.
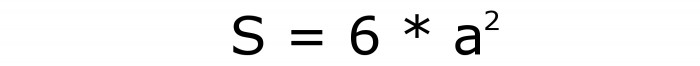
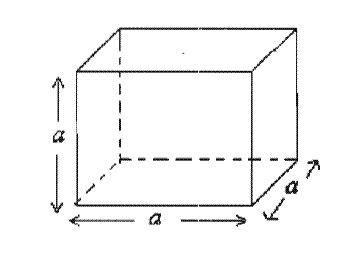
Metodo 2: come calcolare l'area, se si conosce il volume del corpo
Questo metodo si riduce a contare la lunghezza di un bordo di un volume noto. E quindi utilizzare la formula ben nota, che è designata qui dal numero 2.
Ad
Dall'espressione matematica per il volume di un esaedro, si può derivarne uno con il quale si può calcolare la lunghezza del bordo. Eccolo:
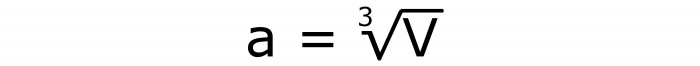
La numerazione continua e qui è il numero 3.
Ora può essere calcolato e sostituito nella seconda formula. Se agiamo secondo le norme della matematica, allora dobbiamo ricavare la seguente espressione:
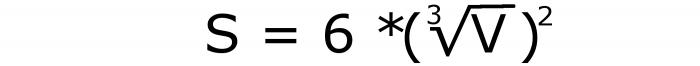
Questa è la formula per l'area dell'intera superficie del cubo, che può essere utilizzata se il volume è noto. Questo numero di registrazione è 4.
Metodo 3: calcolo dell'area sulla diagonale del cubo
Per calcolare l'area dell'intera superficie del cubo, devi anche disegnare un bordo attraverso una diagonale conosciuta. Usa la formula per l'esaedro diagonale principale:
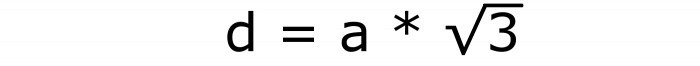
Questa è la formula numero 5.
Da questo, è facile derivare un'espressione per il bordo del cubo:
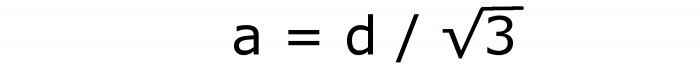
Questa è la sesta formula. Dopo averlo calcolato, puoi usare nuovamente la formula sotto il secondo numero. Ma è meglio scrivere questo:
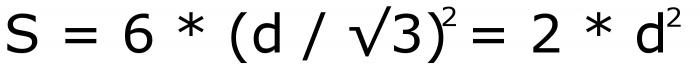
Risulta essere numerato 7. Se osservi attentamente, puoi vedere che quest'ultima formula è più conveniente di un calcolo graduale.
Metodo 4: Come utilizzare il raggio del cerchio inscritto o circoscritto per calcolare l'area del cubo
Se denotiamo il raggio di un cerchio descritto attorno all'exahed dalla lettera R, allora l'area superficiale del cubo sarà facilmente calcolata usando la seguente formula:
Ad
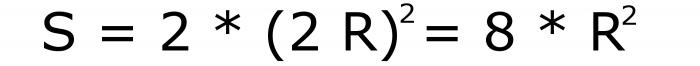
Il suo numero di serie è 8. È facilmente ottenibile grazie al fatto che il diametro del cerchio coincide completamente con la diagonale principale.
Denotando il raggio del cerchio inscritto con la lettera latina r, puoi ottenere la seguente formula per l'area dell'intera superficie dell'esadedro:
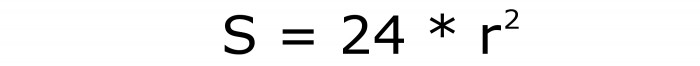
Questa è la formula numero 9.
Alcune parole sulla superficie laterale dell'esadedro
Se il problema richiede di trovare l'area della superficie laterale del cubo, è necessario utilizzare la tecnica già descritta in precedenza. Quando il bordo del corpo è già dato, allora semplicemente il quadrato del quadrato deve essere moltiplicato per 4. Questa figura è apparsa perché ci sono solo 4 facce laterali del cubo. La notazione matematica per questa espressione è:

Il suo numero è 10. Se vengono forniti altri valori, fare lo stesso dei metodi descritti sopra.
Esempi di compiti
La condizione del primo Superficie nota del cubo. È di 200 cm². È necessario calcolare la diagonale principale del cubo.
La decisione
1 via. È necessario utilizzare la formula designata dal numero 2. Da essa sarà semplice dedurre "e". Questa notazione matematica sarà simile radice quadrata dal parziale uguale a S per 6. Dopo la sostituzione dei numeri, otteniamo:
a = √ (200/6) = √ (100/3) = 10 √3 (cm).
La quinta formula consente di calcolare immediatamente la diagonale principale del cubo. Per fare ciò, è necessario moltiplicare il valore del bordo di √3. È semplice La risposta è che la diagonale è di 10 cm.
2 vie. Nel caso in cui la formula per la diagonale sia dimenticata, ma ricordo il teorema di Pitagora.
Allo stesso modo del primo metodo, trova il bordo. Quindi è necessario scrivere due volte il teorema dell'ipotenusa: il primo per il triangolo sul viso, il secondo per quello che contiene la diagonale desiderata.
х² = ² + ², dove x è la diagonale del quadrato.
d² = x² + a² = a² + a² + a² = 3 a². Da questo record è facile vedere come si ottiene la formula per la diagonale. E poi tutti i calcoli saranno, come nel primo metodo. È un po 'più lungo, ma ti consente di non memorizzare la formula, ma di ottenerla da te.
Ad
rispondere: cubo diagonale pari a 10 cm.
La seconda condizione Per una superficie nota, che è uguale a 54 cm 2 , calcola il volume del cubo.
La decisione
Utilizzando la formula sotto il secondo numero, è necessario conoscere il valore del bordo del cubo. Come questo viene fatto è descritto in dettaglio nel primo metodo per risolvere il problema precedente. Dopo tutti i calcoli, otteniamo un a = 3 cm.
Ora è necessario utilizzare la formula per il volume del cubo, in cui la lunghezza del bordo viene aumentata alla terza potenza. Quindi, il volume sarà considerato come: V = 3 3 = 27 cm 3 .
Risposta: il volume del cubo è di 27 cm 3 .

La condizione del terzo. È richiesto di trovare il bordo del cubo per il quale è soddisfatta la seguente condizione. Quando il bordo viene aumentato di 9 unità, l'area dell'intera superficie aumenta di 594.
La decisione
Poiché non ci sono numeri espliciti nel problema, solo la differenza tra ciò che è stato e ciò che è diventato, quindi dovrebbero essere introdotte ulteriori designazioni. È facile Lascia che il valore desiderato sia uguale a "a". Quindi il bordo allargato del cubo sarà (a + 9).
Sapendo questo, è necessario scrivere la formula per la superficie del cubo due volte. Il primo - per il valore iniziale del bordo - coinciderà con quello numerato dal numero 2. Il secondo sarà leggermente diverso. In esso, invece di "a" devi scrivere l'importo (a + 9). Poiché il problema riguarda la differenza di aree, dobbiamo sottrarre l'area più piccola dall'area più ampia:
6 * (a + 9) 2 - 6 * a 2 = 594.
È necessario effettuare la trasformazione. Innanzitutto, estrai 6 nella parte sinistra dell'eguaglianza, quindi semplifica ciò che rimane tra parentesi. Vale a dire (a + 9) 2 - a 2 . Ecco la differenza dei quadrati, che possono essere convertiti come segue: (a + 9 - a) (a + 9 + a). Dopo aver semplificato l'espressione, otteniamo 9 (2a + 9).
Ora deve essere moltiplicato per 6, cioè il numero precedente alla parentesi ed equivale a 594: 54 (2a + 9) = 594. Questo equazione lineare con uno sconosciuto È facile da risolvere. Innanzitutto è necessario aprire le parentesi, quindi spostare l'addendum con un valore sconosciuto sul lato sinistro dell'equazione e i numeri sul lato destro. L'equazione risulterà: 2а = 2. Da esso è visibile che la dimensione richiesta è uguale a 1.
Risposta: a = 1.