Trigonometria da zero: concetti di base, storia

Seno, coseno, tangente - quando pronunciate queste parole in presenza di studenti delle scuole superiori, potete essere sicuri che due terzi di loro perderanno interesse in ulteriori conversazioni. La ragione sta nel fatto che le basi della trigonometria a scuola sono insegnate in completo isolamento dalla realtà, e quindi gli studenti non vedono il punto nello studio di formule e teoremi.

Infatti, a un esame più attento, questa area di conoscenza risulta essere piuttosto interessante, oltre che applicata: la trigonometria trova applicazione in astronomia, costruzione, fisica, musica e molti altri campi.

Facciamo conoscenza con i concetti di base e nomineremo diversi motivi per studiare questa sezione della scienza matematica.

Storia di

Non è noto in quale momento l'umanità abbia iniziato a creare la trigonometria futura da zero. Tuttavia, è stato documentato che già nel secondo millennio aC, gli egiziani avevano familiarità con le basi di questa scienza: gli archeologi hanno trovato un papiro con un compito in cui è necessario trovare l'angolo di inclinazione della piramide su due lati noti.

Un successo più serio fu raggiunto dagli scienziati dell'antica Babilonia. Nel corso dei secoli, facendo astronomia, padroneggiarono un certo numero di teoremi, introdussero modi speciali per misurare gli angoli, che, a proposito, usiamo oggi: gradi, minuti e secondi furono presi in prestito dalla scienza europea nella cultura greco-romana, in cui queste unità provenivano dai Babilonesi.

Si presume che il famoso teorema di Pitagora, relativo alle basi della trigonometria, fosse noto ai babilonesi quasi quattromila anni fa.

nome

Letteralmente, il termine "trigonometria" può essere tradotto come "misurare i triangoli". L'oggetto principale di studio in questa sezione della scienza è stato per molti secoli triangolo rettangolo o meglio, la relazione tra le grandezze degli angoli e le lunghezze dei suoi lati (oggi, lo studio della trigonometria da zero inizia con questa sezione). Ci sono spesso situazioni nella vita in cui è impossibile misurare praticamente tutti i parametri richiesti di un oggetto (o la distanza da un oggetto), e quindi diventa necessario ottenere i dati mancanti tramite calcoli.

Ad esempio, in passato, una persona non poteva misurare la distanza da oggetti spaziali ma i tentativi di calcolare queste distanze si verificano molto prima dell'avvento della nostra era. Anche la trigonometria ha giocato un ruolo importante nella navigazione: avendo una certa conoscenza, il capitano poteva sempre navigare di notte tra le stelle e regolare il percorso.

Concetti di base

Per padroneggiare la trigonometria da zero, è necessario comprendere e ricordare alcuni termini di base.

Il seno di un certo angolo è il rapporto tra la gamba opposta e l'ipotenusa. Chiariamo che la gamba opposta è il lato opposto all'angolo che stiamo considerando. Quindi, se l'angolo è di 30 gradi, il seno di questo angolo sarà sempre, per qualsiasi dimensione del triangolo, essere ½. Il coseno dell'angolo è il rapporto tra la gamba adiacente e l'ipotenusa.

La tangente è il rapporto tra la gamba opposta e quella adiacente (o, in modo equivalente, il rapporto tra seno e coseno). Cotangent è un'unità divisa per tangente.

Vale la pena ricordare il famoso Pi (3.14 ...), che rappresenta la metà circonferenza con un raggio di una unità.

Bug popolari

Le persone che studiano da zero la trigonometria commettono una serie di errori, per lo più per incuria.

In primo luogo, quando si risolvono i problemi in geometria, si deve ricordare che l'uso di seni e coseni è possibile solo in un triangolo rettangolo. Succede che uno studente "sulla macchina" prende il lato più lungo del triangolo per l'ipotenusa e ottiene risultati non corretti dei calcoli.

In secondo luogo, all'inizio è facile confondere i valori di seno e coseno per l'angolo selezionato: ricordiamo che il seno di 30 gradi è numericamente uguale al coseno di 60 e viceversa. Quando si sostituisce il numero sbagliato, tutti gli altri calcoli saranno errati.

In terzo luogo, finché il problema non viene completamente risolto, non è necessario arrotondare alcun valore, estrarre le radici, annotare una frazione ordinaria come decimale. Spesso, gli studenti cercano di ottenere un numero "bello" nel compito di trigonometria e di estrarre immediatamente la radice da tre, sebbene in esattamente una azione questa radice possa essere ridotta.

Etimologia della parola "seno"

La storia della parola "sinus" è davvero insolita. Il fatto è che la traduzione letterale di questa parola dal latino significa "vuoto". Questo perché la corretta comprensione della parola è stata persa quando si traduceva da una lingua all'altra.

I nomi delle funzioni trigonometriche di base provenivano dall'India, dove il concetto di seno era denotato dalla parola "corda d'arco" in sanscrito - il fatto è che il segmento insieme all'arco di un cerchio su cui era basato assomigliava ad un arco. Durante il periodo di massimo splendore della civiltà araba, le conquiste indiane nel campo della trigonometria furono prese in prestito e il termine fu trasferito nella lingua araba sotto forma di trascrizione. Successe che in questa lingua c'era già una parola simile che indicava un vuoto, e se gli arabi capivano la differenza fonetica tra la parola nativa e quella presa in prestito, allora gli europei che traducevano i trattati scientifici in latino traducevano letteralmente la parola araba, nessuna relazione con il concetto di seno . Li usiamo fino ad oggi.

Tabelle dei valori

Ci sono tabelle in cui sono inseriti valori numerici per i seni, i coseni e le tangenti di tutti i possibili angoli. Di seguito presentiamo i dati per angoli di 0, 30, 45, 60 e 90 gradi, che devono essere appresi come una sezione obbligatoria della trigonometria per i manichini, il vantaggio di ricordarli è abbastanza facile.

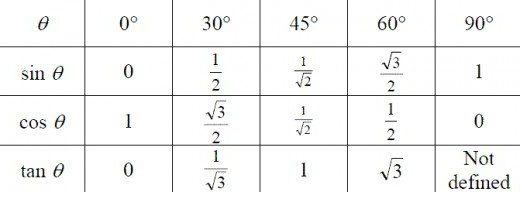Se succede che il valore numerico del seno o coseno dell'angolo "è volato fuori dalla testa", c'è un modo per ricavarlo da solo.

Rappresentazione geometrica

Disegna un cerchio, attraverso il suo centro disegniamo l'ascissa e gli assi delle ordinate. L'asse delle ascisse si trova orizzontalmente, l'asse delle ordinate è verticale. Di solito sono firmati come "X" e "Y", rispettivamente. Ora dal centro del cerchio disegniamo una linea in modo tale da ottenere l'angolo di cui abbiamo bisogno tra esso e l'asse X. Infine, dal punto in cui la retta interseca il cerchio, abbassiamo la perpendicolare all'asse X. La lunghezza del segmento risultante sarà uguale al valore numerico del seno del nostro angolo.

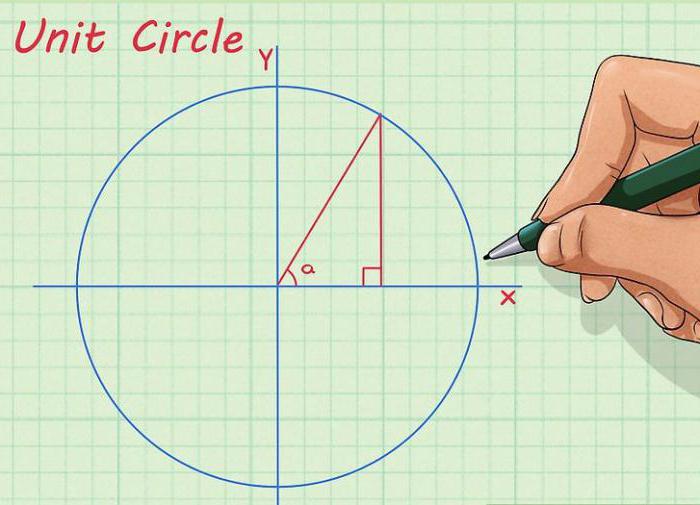Questo metodo è molto rilevante se hai dimenticato il valore desiderato, ad esempio, sull'esame, e non c'è nessun libro di testo sulla trigonometria a portata di mano. Non otterrai una cifra esatta in questo modo, ma sicuramente vedrai la differenza tra 1/2 e 1,73 / 2 (il seno e il coseno di un angolo di 30 gradi).

applicazione

Uno dei primi specialisti a utilizzare la trigonometria erano i marinai che non avevano nessun altro punto di riferimento in mare aperto, tranne il cielo sopra le loro teste. Oggi i capitani delle navi (aerei e altro tipi di trasporto) Non stanno cercando il percorso più breve attraverso le stelle, ma stanno facendo ricorso attivamente alla navigazione GPS, che sarebbe stata impossibile senza l'uso della trigonometria.

In quasi tutti sezione di fisica Stai aspettando calcoli usando seni e coseni: che si tratti dell'applicazione della forza nella meccanica, dei calcoli del percorso degli oggetti nella cinematica, delle oscillazioni, della propagazione delle onde, della rifrazione della luce - non puoi fare a meno della trigonometria di base nelle formule.

Un'altra professione impensabile senza trigonometria è il geometra. Usando un teodolite e un livello o un dispositivo più complesso - un tachimetro, queste persone misurano la differenza di altezza tra i diversi punti sulla superficie terrestre.

frequenza

La trigonometria riguarda non solo gli angoli e i lati del triangolo, sebbene sia stato da questo punto che iniziò la sua esistenza. In tutte le aree dove c'è ciclicità (biologia, medicina, fisica, musica, ecc.) Incontrerai un programma il cui nome probabilmente conosci è l'onda sinusoidale.

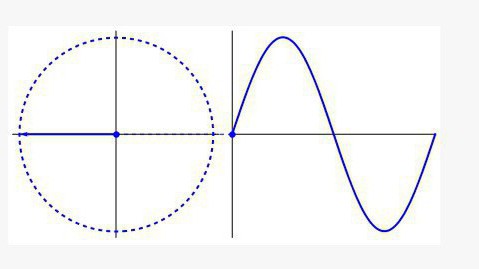Tale grafico è un cerchio sviluppato lungo l'asse del tempo e sembra un'onda. Se hai mai lavorato con un oscilloscopio in un corso di fisica, capisci di cosa si tratta. Sia l'equalizzatore musicale che il dispositivo che visualizza i ritmi cardiaci utilizzano formule di trigonometria nel loro lavoro.

In conclusione

Pensando a come imparare la trigonometria, la maggior parte degli studenti delle scuole medie e superiori comincia a considerarla una scienza complessa e poco pratica, dal momento che vengono a conoscenza solo di noiose informazioni da un libro di testo.

Per quanto riguarda l'impraticabilità - abbiamo già visto che in vari gradi, la capacità di gestire i seni e le tangenti è richiesta in quasi tutti i campi di attività. Per quanto riguarda la complessità ... Pensate: se le persone hanno usato questa conoscenza più di duemila anni fa, quando un adulto aveva meno conoscenze degli studenti delle scuole superiori di oggi, è davvero possibile per voi studiare questo campo della scienza ad un livello base? Alcune ore di lezioni pensate per risolvere i problemi - e raggiungerai il tuo obiettivo studiando il corso base, la cosiddetta trigonometria per i manichini.