Macchina di Turing: descrizione ed esempi di macchine di Turing
La macchina di Turing è una delle scoperte intellettuali più intriganti ed eccitanti del 20 ° secolo. Questo è un semplice e utile modello astratto di calcolo (computer e digitale), che è abbastanza comune per la realizzazione di qualsiasi compito informatico. Grazie a una semplice descrizione e condotta analisi matematica costituisce il fondamento dell'informatica teorica. Questo studio ha portato a una conoscenza più approfondita dei calcolatori e dei calcolatori digitali, compresa la comprensione che ci sono alcuni problemi computazionali che non possono essere risolti sui computer degli utenti comuni. 
Cosa è e chi ha creato
Alan Turing ha cercato di descrivere il modello più primitivo di un dispositivo meccanico che avrebbe le stesse capacità di base di un computer. Turing descrisse per la prima volta l'auto nel 1936 nell'articolo "Sui numeri computabili con un'applicazione al problema della risolvibilità", che apparve negli Atti della London Mathematical Society. 
Una macchina di Turing è un dispositivo di calcolo costituito da una testina di lettura / scrittura (o "scanner") con un nastro di carta che lo attraversa. Il nastro è diviso in quadrati, ognuno dei quali porta un singolo carattere - "0" o "1". Lo scopo del meccanismo è che agisce sia come mezzo per entrare e uscire, sia come memoria di lavoro per memorizzare i risultati di passaggi computazionali intermedi.
In cosa consiste il dispositivo
Ciascuna di queste macchine è composta da due componenti:
- Nastro illimitato. È infinito in entrambe le direzioni e diviso in celle.
- Programma controllato automaticamente, scanner a testa per leggere e scrivere dati. Può essere in ogni momento in uno dei tanti stati.
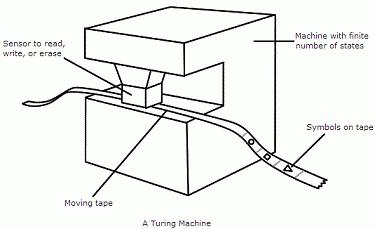
Ogni macchina collega due serie di dati finiti: l'alfabeto dei simboli in entrata A = {a0, a1, ..., am} e l'alfabeto degli stati Q = {q0, q1, ..., qp}. Lo stato q0 è chiamato passivo. Si ritiene che il dispositivo finisca il suo lavoro quando cade su di lui. Lo stato di q1 è chiamato iniziale - la macchina inizia i suoi calcoli, essendo all'inizio in esso. La parola di input si trova sul nastro una lettera di fila in ogni posizione. Su entrambi i lati ci sono solo celle vuote.
Come funziona il meccanismo
La macchina di Turing ha una differenza fondamentale rispetto ai dispositivi di calcolo: il suo dispositivo di memoria ha un nastro infinito, mentre per i dispositivi digitali questo dispositivo ha una striscia di una certa lunghezza. Ogni classe di compiti è risolta solo da una macchina di Turing costruita. Altri tipi di compiti implicano la scrittura di un nuovo algoritmo.
Il dispositivo di controllo, essendo in uno stato, può muoversi in qualsiasi direzione lungo la cintura. Scrive nelle celle e legge da loro i caratteri dell'alfabeto finale. Nel processo di spostamento, viene selezionato un elemento vuoto che riempie le posizioni che non contengono dati di input. L'algoritmo per la macchina di Turing determina le regole di transizione per il dispositivo di controllo. Impostano la testina di lettura-scrittura sui seguenti parametri: scrittura su una cella di un nuovo carattere, passaggio a un nuovo stato, spostamento a sinistra oa destra lungo il nastro. 
Proprietà del meccanismo
La macchina di Turing, come altri sistemi di calcolo, ha le sue caratteristiche intrinseche e sono simili alle proprietà degli algoritmi:
- Discrete. La macchina digitale procede al passaggio successivo n + 1 solo dopo aver completato quello precedente. Ogni passo completato assegna ciò che sarà n + 1.
- Comprensibilità. Il dispositivo esegue solo un'azione per la stessa cella. Inserisce un carattere dall'alfabeto e fa un movimento: a sinistra oa destra.
- Determinismo. Ogni posizione nel meccanismo corrisponde a una singola forma di realizzazione dello schema specificato, e in ogni fase dell'azione e la sequenza della loro esecuzione non è ambigua.
- Efficacia. Il risultato esatto per ogni stadio è determinato dalla macchina di Turing. Il programma esegue l'algoritmo e in un numero finito di passaggi entra nello stato q0.
- Mass. Ogni dispositivo è definito sopra le parole valide nell'alfabeto.
Funzioni della macchina di Turing
La soluzione di algoritmi richiede spesso l'implementazione di una funzione. A seconda della possibilità di scrivere una catena per il calcolo, la funzione viene definita algoritmicamente risolvibile o insolubile. Come insieme di numeri naturali o razionali, parole nell'alfabeto N finito per una macchina, viene considerata la sequenza dell'insieme B - parole all'interno dell'alfabeto di codice binario B = {0.1}. Il risultato del calcolo tiene conto anche del valore "non definito" che si verifica quando l'algoritmo si blocca. Per implementare la funzione, è importante avere un linguaggio formale nell'alfabeto finale e la risolubilità del problema di riconoscere le descrizioni corrette. 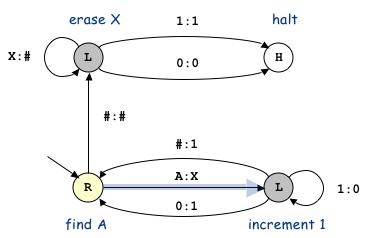
Programma per il dispositivo
I programmi per il meccanismo di Turing sono formati da tabelle in cui la prima riga e colonna contengono i caratteri dell'alfabeto esterno e i valori dei possibili stati interni dell'automa - l'alfabeto interno. I dati tabulari sono comandi che vengono percepiti dalla macchina di Turing. La soluzione dei problemi si verifica in questo modo: la lettera letta dalla testa nella cella su cui si trova attualmente, e lo stato interno della testa dell'automa determina quale comando deve essere eseguito. Nello specifico, tale comando si trova all'incrocio tra i simboli dell'alfabeto esterno e quello interno, che sono nella tabella. 
Componenti per i calcoli
Per costruire una macchina di Turing per risolvere un compito specifico, è necessario determinare i seguenti parametri per esso.
Alfabeto esterno Questo è un insieme finito di simboli, indicato dal segno A, i cui elementi costitutivi sono chiamati lettere. Uno di questi - a0 - deve essere vuoto. Ad esempio, l'alfabeto di un dispositivo di Turing che funziona con numeri binari assomiglia a questo: A = {0, 1, a0}.
Una sequenza continua di caratteri alfanumerici scritti su nastro viene chiamata una parola.
Una macchina automatica è un dispositivo che funziona senza intervento umano. Nella macchina di Turing, ha diversi stati diversi per risolvere i problemi e, in determinate condizioni, si sposta da una posizione all'altra. La combinazione di tali stati della carrozza è un alfabeto interno. Ha una designazione di lettera del modulo Q = {q1, q2 ...}. Una di queste disposizioni - q1 - dovrebbe essere quella iniziale, cioè, ciò che avvia il programma. Un altro elemento necessario è lo stato q0, che è finito, cioè completa il programma e pone il dispositivo nella posizione di stop.
Tabella di conversione Questo componente è un algoritmo per il comportamento del carrello del dispositivo, a seconda dello stato corrente della macchina e del valore del simbolo letto. 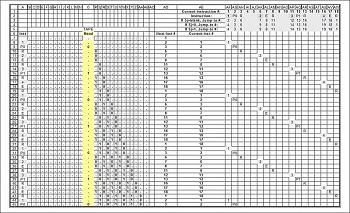
Algoritmo per automa
Il trasporto del dispositivo di Turing durante il funzionamento è controllato dal programma, che durante ciascuna fase esegue la sequenza delle seguenti azioni:
- Scrivere un carattere di alfabeto esterno in una posizione, incluso uno vuoto, sostituendo un elemento che era in esso, incluso uno vuoto.
- Sposta un passo a sinistra o a destra.
- Cambia il tuo stato interiore.
Pertanto, quando si scrivono programmi per ogni coppia di caratteri o posizioni, è necessario descrivere con precisione tre parametri: un elemento i dell'alfabeto A selezionato, direzione dello spostamento del carrello ("←" a sinistra, "→" a destra, "punto" - nessun movimento) e q k è il nuovo stato del dispositivo.Ad esempio, il comando 1 "←" q 2 è impostato su "sostituire il carattere con 1, spostare la testina del carrello a sinistra di una cella di passaggio e effettuare la transizione allo stato q 2 ".
Macchina di Turing: esempi
Esempio 1. Dato il compito di costruire un algoritmo che aggiunge uno all'ultima cifra di un dato numero che si trova sul nastro. Dati di input - parola - cifre dell'intero numero decimale, scritti in celle successive sul nastro. Nel momento iniziale il dispositivo si trova di fronte al simbolo più a destra - la cifra del numero.
La decisione Se l'ultima cifra è uguale a 9, deve essere sostituita con 0 e quindi aggiungerne una al carattere precedente. Il programma in questo caso per questo dispositivo di Turing può essere scritto in questo modo:
| a 0 | 0 | 1 | 2 | 3 | ... | 7 | 8 | 9 | |
| q 1 | 1 H q 0 | 1 H q 0 | 2 H q 0 | 3 H q 0 | 4 H q 0 | ... | 8 H q 0 | 9 H q 0 | 0 λ q 1 |
Qui q 1 è lo stato di modifica della cifra, q 0 è la fermata. Se in q 1 l' automaton corregge un elemento della serie 0..8, lo sostituisce con uno di 1..9, rispettivamente, e poi passa allo stato q 0 , cioè il dispositivo si ferma. Se il carrello corregge il numero 9, lo sostituisce con 0, quindi si sposta a sinistra, fermandosi nello stato q 1 . Questo movimento continua finché il dispositivo non corregge una cifra inferiore a 9. Se tutti i caratteri sono uguali a 9, vengono sostituiti con zeri, 0 viene sostituito con l'elemento iniziale, il carrello si sposterà a sinistra e scriverà 1 in una cella vuota. Il prossimo passo sarà la transizione allo stato q 0 - stop.
Esempio 2. Data una serie di caratteri che indicano parentesi di apertura e chiusura. È necessario costruire un dispositivo di Turing che rimuova una coppia di parentesi reciproche, cioè elementi disposti in fila - "()". Ad esempio, i dati iniziali: ") (() (()", la risposta dovrebbe essere: ") .. ((" Soluzione: il meccanismo, essendo in q 1 , analizza l'elemento più a sinistra nella linea.
| a 0 | ( | ) | |
| q 1 | a 0 H q 0 | (P q 2 | ) P q 1 |
| q 2 | a 0 H q 0 | (P q 2 | ) λ q 3 |
| q 3 | a 0 H q 0 | a 0 n q 3 | a 0 n q1 |
Stato q 1 : se viene rilevato il simbolo "(", quindi spostare a destra e passare alla posizione q 2 , se "a 0 " è definito, quindi fermarsi.
Stato q 2 : viene eseguita l'analisi della parentesi "(" per la presenza di una coppia, in caso di coincidenza dovrebbe risultare ")". Se l'elemento è una coppia, fai un ritorno a capo a sinistra e vai a q 3 .
Stato q 3 : cancella prima il simbolo "(", quindi "") e vai a q 1 .