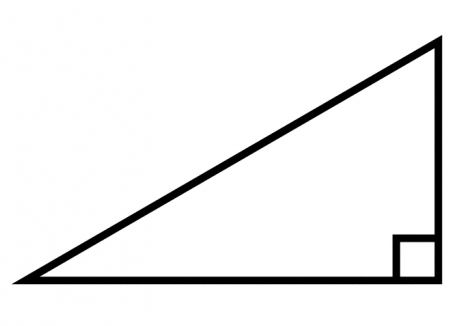
Tipi di triangoli. Angoli triangolari

Il poligono più semplice studiato a scuola è un triangolo. È più comprensibile per studenti e incontri meno difficoltà. Nonostante il fatto che ci sono diversi tipi di triangoli, che hanno proprietà speciali.

Quale forma è chiamata triangolo?

Formata da tre punti e segmenti. I primi sono chiamati vertici, i secondi lati. Inoltre, tutti e tre i segmenti dovrebbero essere collegati per formare degli angoli tra di loro. Da qui il nome della figura "triangolo".

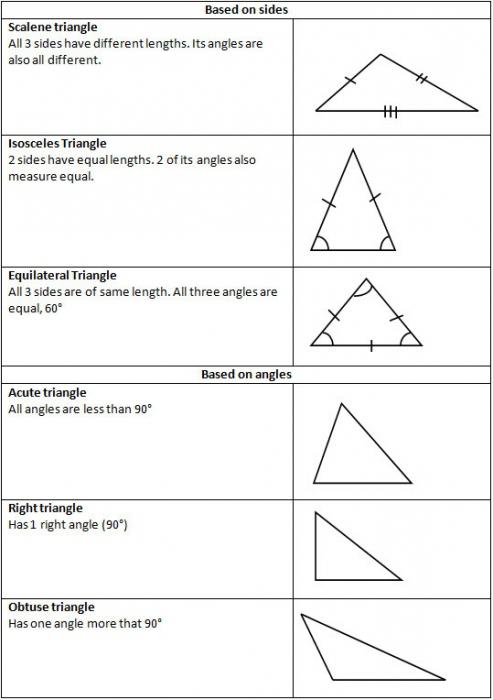
Differenze nei nomi degli angoli

Dal momento che possono essere taglienti, smussati e diritti, i tipi di triangoli sono determinati da questi nomi. Di conseguenza, ci sono tre gruppi di tali figure.

• Il primo Se tutti gli angoli del triangolo sono acuti, allora avrà il nome di un angolo acuto. Tutto è logico.

• Il secondo Uno degli angoli è ottuso, il che significa un angolo triangolare. Semplicemente non c'è posto.

• Terzo. C'è un angolo di 90 gradi, che è chiamato diritto. Il triangolo diventa rettangolare.

Differenze nei nomi ai lati

A seconda delle caratteristiche dei lati, questi tipi di triangoli si distinguono:

• il caso generale è versatile, in cui tutti i lati hanno una lunghezza arbitraria;

• isoscele, i cui lati hanno gli stessi valori numerici;

• equilatero, le lunghezze di tutti i suoi lati sono le stesse.

Se l'attività non specifica un tipo specifico di triangolo, è necessario disegnarne uno arbitrario. In cui tutti gli angoli sono nitidi e i lati hanno lunghezze diverse.

Proprietà comuni a tutti i triangoli

1. Se sommi tutti gli angoli del triangolo, ottieni un numero uguale a 180º. E non importa come sia. Questa regola è sempre valida.
2. Il valore numerico di entrambi i lati del triangolo è inferiore rispetto agli altri due aggiunti insieme. Allo stesso tempo, è più della loro differenza.
3. Ogni angolo esterno ha un valore che si ottiene aggiungendo due interni, non adiacenti ad esso. Inoltre, è sempre più di quello interno adiacente ad esso.
4. Di fronte al lato più piccolo del triangolo c'è sempre l'angolo più piccolo. Viceversa, se il lato è grande, allora l'angolo sarà il più grande.

Queste proprietà sono sempre valide, indipendentemente dal tipo di triangoli considerati nei problemi. Tutti gli altri seguono da caratteristiche specifiche.

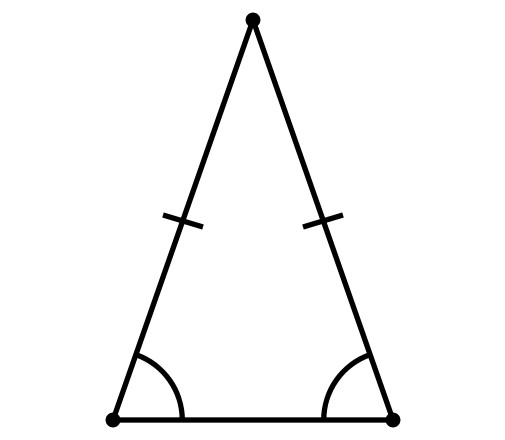
Proprietà di un triangolo isoscele

• Gli angoli che sono adiacenti alla base sono uguali.
• L'altezza che si tiene alla base è anche la mediana e la bisettrice.
• Le altezze, le mediane e le bisettrici che sono costruite ai lati del triangolo sono rispettivamente uguali tra loro.

Proprietà di un triangolo equilatero

Se c'è una tale figura, allora tutte le proprietà sopra descritte saranno vere. Perché l'equilatero sarà sempre isoscele. Ma non il contrario, un triangolo isoscele non sarà necessariamente equilatero.

• Tutti i suoi angoli sono uguali tra loro e hanno un valore di 60º.
• Qualsiasi mediana di un triangolo equilatero è la sua altezza e una bisettrice. E sono tutti uguali tra loro. Per determinare i loro valori, c'è una formula che consiste nel prodotto di una festa radice quadrata da 3 diviso per 2.

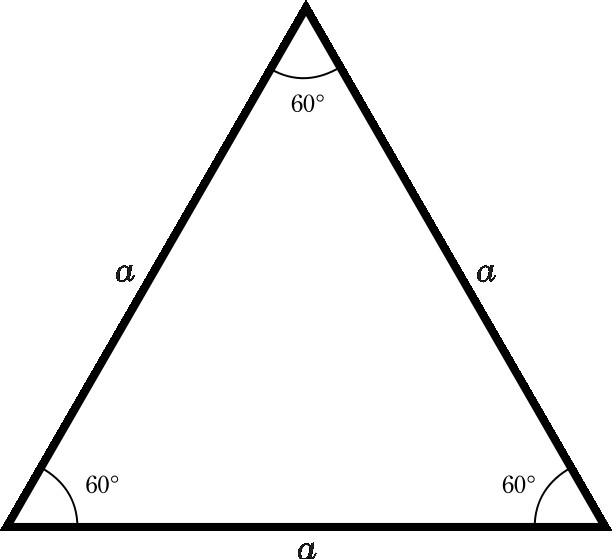
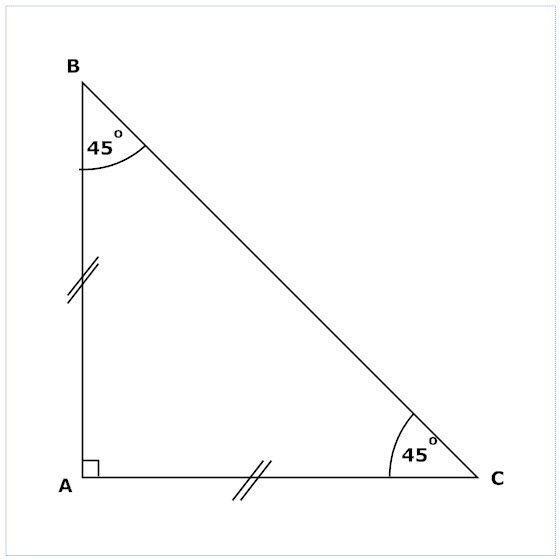
Proprietà di un triangolo rettangolo

• Due angoli acuti danno un valore totale di 90º.
• La lunghezza dell'ipotenusa è sempre maggiore di quella di una qualsiasi delle gambe.
• Il valore numerico della mediana condotta per l'ipotenusa è la metà di esso.
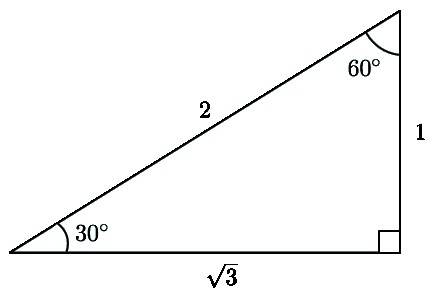
• Lo stesso valore è uguale alla gamba, se si trova di fronte all'angolo di 30º.
• L'altezza, che viene disegnata dall'alto con un valore di 90 °, ha una certa dipendenza matematica dalle gambe: 1 / n ² = 1 / a ² + 1 / in ² . Qui: a, c - gambe, altezza n.

Compiti con diversi tipi di triangoli

№1. Viene dato un triangolo isoscele. Il suo perimetro è noto ed è di 90 cm. È necessario conoscerne i lati. Come condizione aggiuntiva: il lato è inferiore alla base di 1,2 volte.

decisione

Il valore del perimetro dipende direttamente dai valori che devono essere trovati. La somma di tutti e tre i lati darà 90 cm. Ora dobbiamo ricordare il segno del triangolo, in cui è isoscele. Cioè, le due parti sono uguali. Puoi creare un'equazione con due incognite: 2a + b = 90. Qui a è il lato, nella - base.

È il turno di una condizione aggiuntiva. Seguendolo, si ottiene la seconda equazione: в = 1,2а. Puoi sostituire questa espressione nel primo. Risulta: 2a + 1.2a = 90. Dopo le trasformazioni: 3.2a = 90. Da qui a = 28.125 (cm). Ora è facile scoprire le basi. È meglio farlo dalla seconda condizione: c = 1,2 * 28,125 = 33,75 (cm).

Per controllare, puoi aggiungere tre valori: 28.125 * 2 + 33.75 = 90 (cm). È giusto

Risposta: i lati del triangolo sono 28,125 cm, 28,125 cm, 33,75 cm.

№2. Il lato di un triangolo equilatero è di 12 cm. È necessario calcolarne l'altezza.

La decisione Per cercare una risposta, è sufficiente tornare al punto in cui sono state descritte le proprietà del triangolo. Questa è la formula per trovare l'altezza, la mediana e la bisettrice di un triangolo equilatero.

n = a * √3 / 2, dove n è l'altezza e a è il lato.

La sostituzione e il calcolo danno il seguente risultato: n = 6 √3 (cm).

Questa formula non ha bisogno di essere ricordata. Basti ricordare che l'altezza divide il triangolo in due rettangolari. Inoltre, risulta essere una gamba, e l'ipotenusa in essa è il lato dell'originale, la seconda parte è metà del lato conosciuto. Ora devi scrivere il teorema di Pitagora e ricavare una formula per l'altezza.

Risposta: l'altezza è di 6 √3 cm.

№3. È dato MKR - un triangolo, 90 gradi in cui fa l'angolo K. I lati di MR e KR sono noti, sono uguali rispettivamente a 30 e 15 cm. È necessario apprendere il valore di un angolo R.

La decisione Se fai un disegno, diventa chiaro che MR è un'ipotenusa. Ed è il doppio della gamba del KR. Ancora una volta è necessario fare riferimento alle proprietà. Uno di questi è collegato con gli angoli. Da esso è chiaro che l'angolo del CMR è pari a 30º. Quindi l'angolo P desiderato sarà uguale a 60º. Questo deriva da un'altra proprietà, che afferma che la somma di due angoli acuti dovrebbe essere di 90º.

Risposta: l'angolo P è 60º.

№4. Hai bisogno di trovare tutti gli angoli di un triangolo isoscele. Su di lui è noto che l'angolo esterno dall'angolo alla base è 110º.

La decisione Poiché viene dato solo l'angolo esterno, questo dovrebbe essere usato. Si forma con l'interno angolo spiegato. Quindi, in totale, daranno 180º. Cioè, l'angolo alla base del triangolo sarà uguale a 70º. Poiché è isoscele, la seconda angolazione ha lo stesso significato. Resta da calcolare il terzo angolo. Per la proprietà comune a tutti i triangoli, la somma degli angoli è 180º. Quindi, il terzo è definito come 180º - 70º - 70º = 40º.

Risposta: gli angoli sono 70º, 70º, 40º.

№5. È noto che in un triangolo isoscele l'angolo che si trova di fronte alla base è di 90º. Basato sul punto segnato. Il segmento che lo collega con un angolo retto lo divide nel rapporto da 1 a 4. È necessario conoscere tutti gli angoli del triangolo più piccolo.

La decisione Uno degli angoli può essere identificato immediatamente. come triangolo rettangolo e isoscele, quindi quelli che giacciono alla sua base saranno a 45 °, cioè a 90 ° / 2.

Il secondo di loro aiuterà a trovare il conosciuto nella relazione di condizione. Poiché è uguale a 1 a 4, allora le parti in cui è diviso si ottengono solo 5. Pertanto, per scoprire l'angolo più piccolo di un triangolo, è necessario 90º / 5 = 18º. Resta da imparare il terzo. Per fare ciò, da 180º (la somma di tutti gli angoli del triangolo), sottrai 45º e 18º. I calcoli sono semplici e risulteranno: 117º.

Risposta: 18º, 45º, 117º