Teorema di Vieta: esempi del suo uso quando si lavora con equazioni di secondo grado
Quando si studiano i metodi per risolvere le equazioni del secondo ordine in un corso di algebra scolastico, considerare le proprietà delle radici ottenute. Sono attualmente conosciuti come il teorema di Viet. Esempi del suo uso sono indicati in questo articolo.
Equazione quadratica
L'equazione del secondo ordine è un'equazione, che è mostrata nella foto qui sotto.
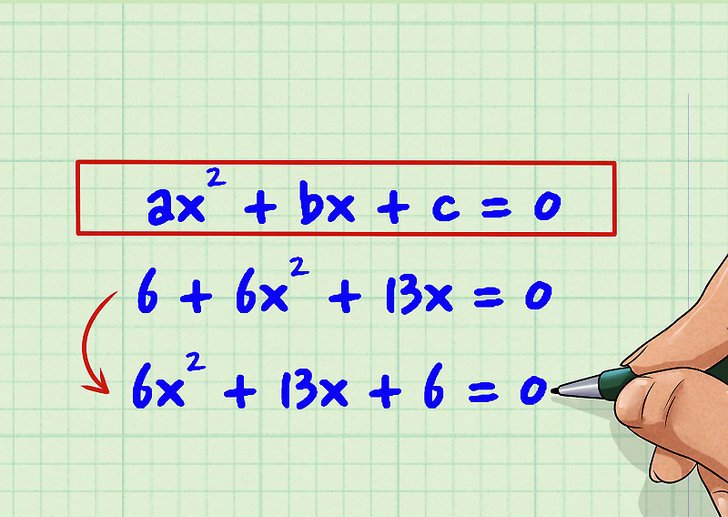
Qui i simboli a, b, c sono alcuni numeri che sono chiamati i coefficienti dell'equazione in questione. Per risolvere l'uguaglianza, è necessario trovare i valori di x che lo rendono vero.
Si noti che poiché il valore massimo del grado di elevazione di X è uguale a due, anche il numero di radici nel caso generale è uguale a due.
Ci sono diversi modi per risolvere questo tipo di uguaglianza. In questo articolo consideriamo uno di questi, che prevede l'uso del cosiddetto teorema di Viet.
Formulazione del teorema di Viet

Alla fine del XVI secolo, il famoso matematico Francois Vietta (francese) notò, analizzando le proprietà delle radici di varie equazioni di secondo grado, che certe combinazioni di esse soddisfano particolari relazioni. In particolare, queste combinazioni sono il loro prodotto e somma.
Il teorema di Vieta stabilisce quanto segue: le radici di un'equazione quadratica con la loro somma danno il rapporto tra coefficienti lineari e quadratici presi con il segno opposto, e quando vengono prodotti, portano al rapporto tra il termine libero e il coefficiente quadratico.
Ad
Se la forma generale dell'equazione è scritta come presentata nella foto nella sezione precedente dell'articolo, allora questo teorema matematico può essere scritto sotto forma di due uguaglianze:
- r 2 + r 1 = -b / a;
- r 1 x r 2 = c / a.
Dove r 1 , r 2 è il valore delle radici dell'equazione in questione.
Queste due equazioni possono essere utilizzate per risolvere un numero di problemi matematici molto diversi. L'uso del teorema di Viet negli esempi con la soluzione è riportato nelle sezioni seguenti dell'articolo.
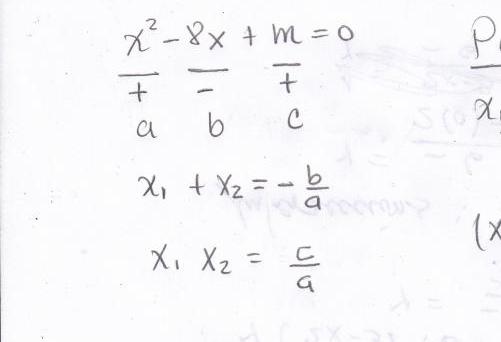
Problema numero 1: ripristinare l'equazione
Presentiamo il seguente problema sull'uso del teorema di Viet. Un esempio dell'equazione è dato come segue: -3.4 * x - 3 * s * x 2 + k = 0. Devi trovare i valori di s e k, sapendo che due numeri sono le soluzioni di questa equazione: -1,2 e 4.
Per prima cosa devi decidere il valore dei coefficienti in questa espressione. Ne consegue che a = -3 * s, b = -3,4 e c = k.
Ora puoi usare il teorema di Viet. Per la somma delle radici, otteniamo la seguente uguaglianza: -1.2 + 4 = - (- 3.4) / (-3 * s), da cui otteniamo che s = -0.40476 (si raccomanda di usare una calcolatrice per calcolare questa espressione). Cioè, a = -3 * s = 1.21429. Per produrre radici abbiamo:
Ad
(-1,2) * 4 = k / 1,21429, da cui k = -5,82859.
L'equazione ricostruita corrisponderà alla forma: -3.4 * x + 1.21429 * x 2 - 5.82859 = 0. Per verificare se il problema è stato risolto correttamente e se c'è un errore nel risolverlo, è necessario sostituire i valori root noti nell'espressione ripristinata. Otteniamo: -3.4 * (-1.2) + 1.21429 * (-1.2) 2 - 5.82859 = 0.00001 ≈ 0 e -3.4 * (4) + 1.21429 * ( 4) 2 - 5.82859 = 0,00005 ≈ 0.
Come vediamo, le uguaglianze ottenute sono effettivamente soddisfatte. Un piccolo errore è dovuto al fatto che durante il ripristino dell'equazione, abbiamo arrotondato i numeri risultanti a 5 cifre decimali.
Problema numero 2: trova le radici dell'equazione
La soluzione delle equazioni quadratiche con il teorema di Viet (vedere un esempio qui sotto) è possibile in non tutti i casi. Cioè, questo metodo non è universale, perché se i coefficienti dell'equazione risultano essere "scomodi", allora non funzionerà.
Ad
I metodi universali per risolvere questo tipo di espressione sono l'uso di una discriminante o aggiunta a un quadrato completo. Tuttavia, l'importanza del teorema di Viet in questo caso è che consente di indovinare le radici sconosciute senza eseguire complicati calcoli matematici.
Ad esempio, viene fornita la seguente espressione: -x 2 + 2 * x + 3 = 0. Dovremmo usare il teorema di Vieta per trovare soluzioni a questa uguaglianza. Lascia che le sue radici siano i numeri r 1 e r 2 . Quindi puoi scrivere il seguente sistema di equazioni:
r 1 + r 2 = -2 / (- 1) = 2;
r 1 * r 2 = 3 / (-1) = -3.
Ora è necessario indovinare quale somma dei numeri è due e il loro prodotto sarà -3. Ovviamente, questi sono i numeri 3 e -1. Saranno le radici dell'equazione.
Se analizziamo un po 'l'argomento, va notato che qualsiasi equazione del secondo ordine, che è facilmente rappresentata come un prodotto di due fattori, può essere risolta con l'aiuto del teorema in discussione. Infatti, in questo caso possiamo scrivere (3-x) * (x + 1), se espandiamo le parentesi, otteniamo l'espressione originale.
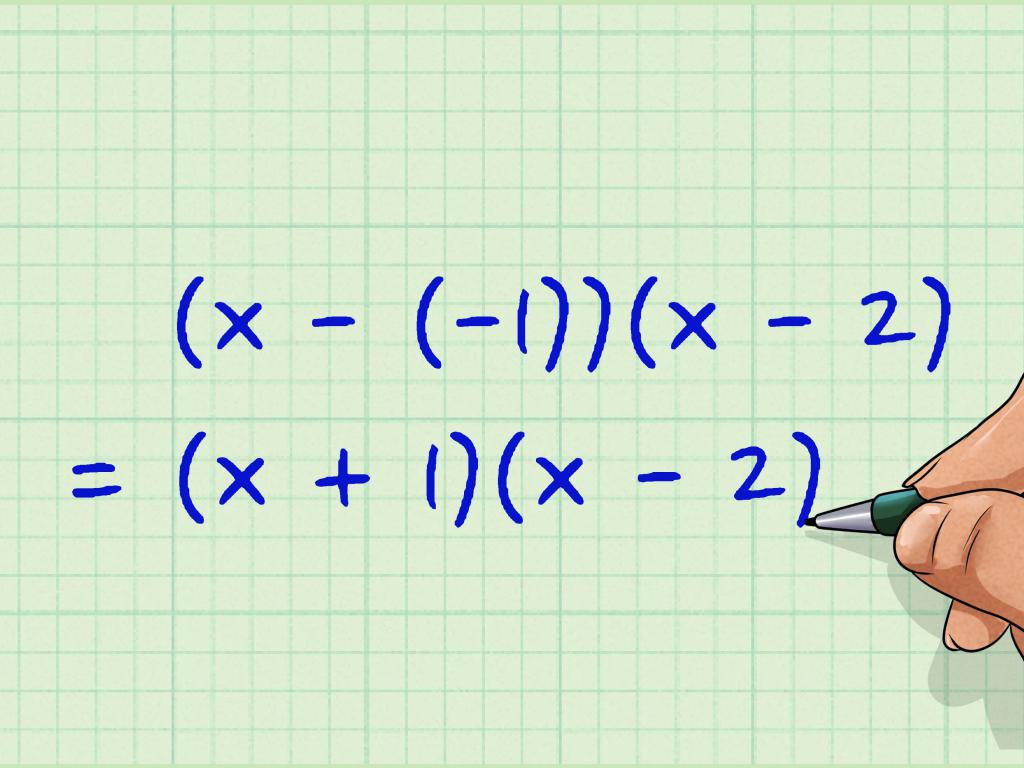
Problema numero 3: la somma dei quadrati
Diamo un altro esempio del teorema di Viet con una soluzione. Data l'equazione:
6 * x 2 - 13 * x + 11 = 0. È necessario trovare la somma dei quadrati delle sue due radici, cioè (r 1 ) 2 + (r 2 ) 2 .
Naturalmente, è possibile risolvere prima questa equazione in uno dei modi e quindi rispondere alla domanda del problema. Tuttavia, se ricordiamo il teorema di Viet e la proprietà del quadrato di somma, allora non ce n'è bisogno.
Ad
Va ricordato come viene calcolata la somma di due numeri al quadrato. Quindi scopriamo che per trovare la somma dei quadrati sconosciuta, è necessario calcolare il valore dell'espressione (r 1 + r 2 ) 2 - 2 * r 1 * r 2 . Usiamo entrambe le uguaglianze del teorema considerato, otteniamo: (13/6) 2 - 2 * 11/6 = 1,02 (7) (7 nel periodo).
Quindi, applicando il teorema di Viet, abbiamo risparmiato tempo nel risolvere l'equazione. In generale, le proprietà delle radici possono essere utilizzate per qualsiasi attività che implichi il calcolo delle loro varie combinazioni.