Cos'è un cono? Concetto e foto
La stereometria è una sezione importante della geometria, l'oggetto di studio di quali sono le proprietà e le caratteristiche delle figure nello spazio tridimensionale. In questo articolo considereremo una di queste cifre volumetriche. Facciamo la conoscenza di cosa sia un cono.
Cono
Diamo la definizione più generale di un cono. Sotto questa figura, comprendiamo la superficie, che si forma come risultato del collegamento di segmenti retti di un certo punto nello spazio con tutti i punti di una data curva. In questo caso, il punto specificato nello spazio non dovrebbe essere nel piano della curva. Ad esempio, se una curva ha la forma di una parabola, la figura ottenuta con il metodo descritto sarà chiamata cono parabolico, se la curva è un'ellisse, il cono sarà ellittico e così via.
Ad
Dopo aver dato una definizione geometrica di cosa sia un cono, presentiamo una foto che mostra le forme visivamente possibili di questa figura.

Guardando questa foto, molti videro in esso la forma di un cappello per bambini, che indossava Buratino, una tazza di cialda dal gelato a forma di corno o un arancio avvertimento e un cono stradale a strisce nere.

Cono di elementi geometrici
Per comprendere meglio la domanda su cosa sia un cono, si dovrebbero citare i nomi geometrici degli elementi di questa figura spaziale.
Il cono è delimitato da due superfici. Il primo è chiamato la base. È un piano che è delimitato dalla curva sopra annotata. Ad esempio, può essere un cerchio o un'ellisse. La seconda superficie è il lato per la forma ed è chiamata conica. Non giace sullo stesso piano, ma può essere trasformato in una figura piatta, come verrà discusso di seguito.
Ad
Uno degli elementi importanti del cono è il suo top. Questo punto delimita la superficie conica. Tutti i punti della curva di base sono collegati ad esso.
Il segmento che collega la parte superiore della base, chiamata generatrice, o che forma un cono. A sua volta, la curva che delimitava la base era chiamata direttrice o figura di guida.
Le aree della superficie e della base coniche si sommano alla superficie totale del cono. Il volume di spazio che queste due superfici limitano è il volume del cono.
Cono cilindrico tondo e sue caratteristiche lineari
Sopra è stata data una definizione generale di cosa sia un cono. Tuttavia, spesso nella pratica e nei problemi geometrici c'è una forma specifica di questa figura: un cono circolare dritto. È mostrato sotto.
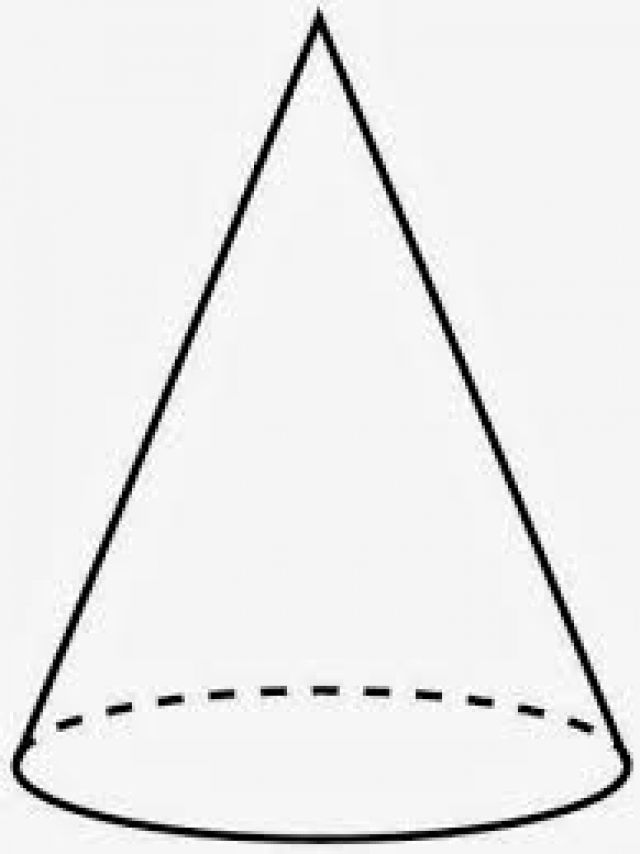
La base di questa figura è un cerchio. Si chiama dritto perché la perpendicolare scesa alla sua base da un'altezza interseca il cerchio nel suo centro esatto. Se questa condizione non fosse soddisfatta, allora potremmo parlare di un cono inclinato.
La linea che collega la cima al centro del cerchio è chiamata l'asse della figura. È anche l'asse di rotazione del cono. Infatti, se prendi un triangolo rettangolo e inizi a ruotarlo attorno a una delle gambe, la figura risultante sarà un cono diritto con una base rotonda. Questo metodo per ottenere un cono è mostrato schematicamente di seguito.
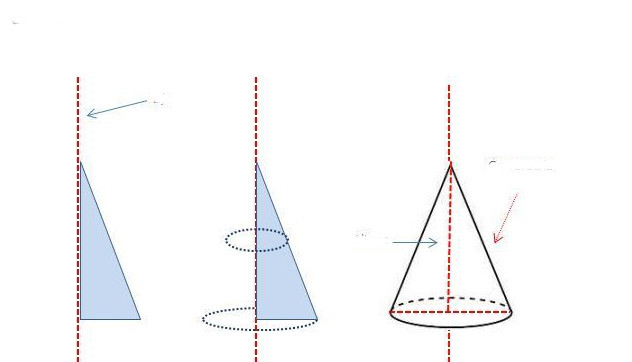
Si può vedere che il generatore sarà uguale alla lunghezza dell'ipotenusa del triangolo. La gamba attorno alla quale è stata eseguita la rotazione diventerà l'altezza della figura tridimensionale e la seconda gamba sarà uguale al raggio del cono (il raggio della base circolare).
Una delle caratteristiche importanti della figura in questione è che le lunghezze di tutti i generatori per essa sono uguali tra loro. Questo fatto ci consente, utilizzando il teorema di Pitagora, di scrivere la connessione matematica tra i tre parametri lineari principali della forma:
Ad
g 2 = r 2 + h 2
Il quadrato del generatore di un cono circolare dritto è uguale alla somma dei quadrati del suo raggio r e altezza h.
Dopo aver esaminato la domanda su che cosa è un cono una retta con una base circolare, mostriamo come è possibile la sua area superficiale e il suo volume.
Determinazione della superficie
Come già notato, la superficie della figura è formata da una superficie conica e una base piatta. Qual è la loro area? Con sicurezza, puoi rispondere a questa domanda se osservi una scansione piatta di un cono circolare. Tagliando la base dalla superficie laterale e tagliando quest'ultima lungo la generatrice, otteniamo il seguente risultato.
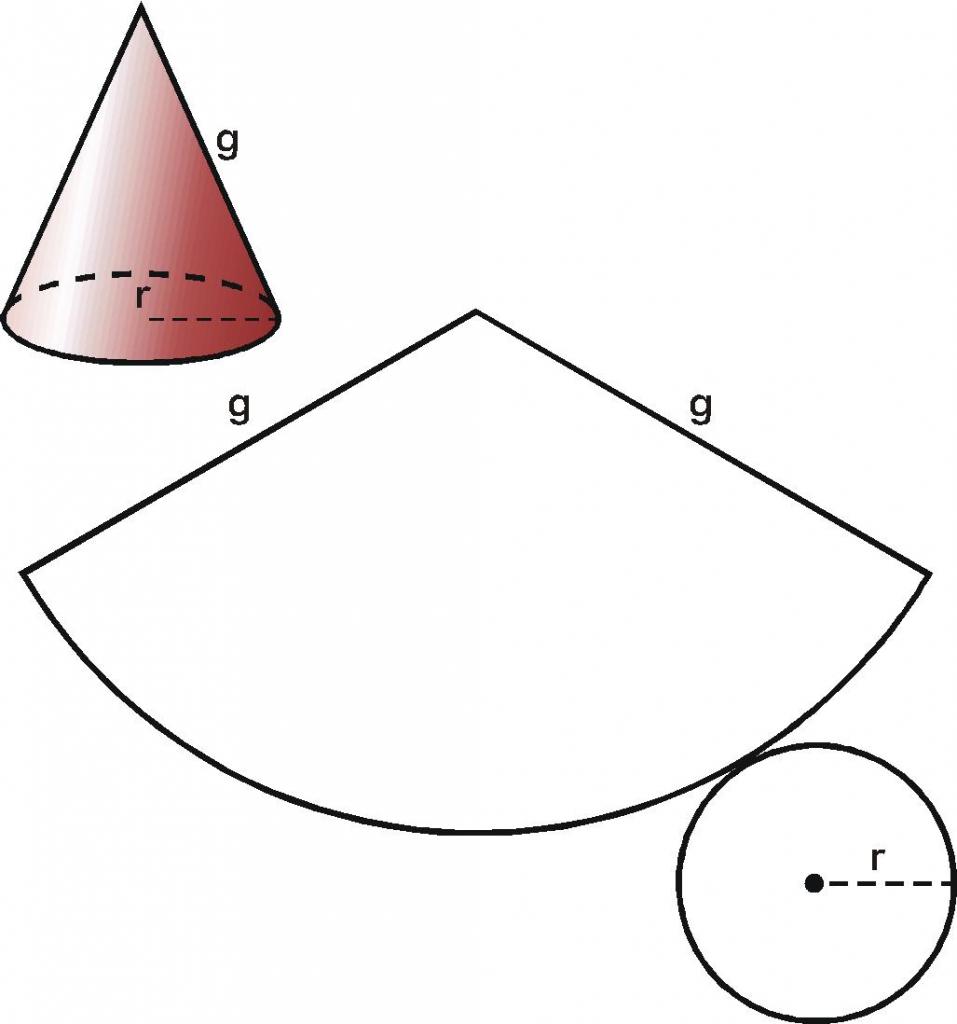
Non ci sono problemi nel determinare l'area di un cerchio. La formula per la sua area è familiare a tutti gli studenti. Scrivilo:
S o = pi * r 2
Il simbolo S o è l'area della base della figura.
La superficie laterale del cono su una scansione piatta è rappresentata da un settore circolare il cui raggio è uguale alla lunghezza del generatore e la lunghezza dell'arco su cui poggia il settore è uguale alla lunghezza della circonferenza della base. Questi dati ci consentono di determinare in modo univoco l'area del settore. Non forniremo calcoli intermedi per ottenere una formula per il quadrato S b della superficie laterale del cono. Scriviamo il risultato finale:
Ad
S b = pi * g * r
Poiché la generatrice g è sempre più grande del raggio r, l'area della superficie laterale della figura, per qualsiasi parametro, supererà quella della base.
La formula per l'area totale assume la forma:
S = S o + S b = pi * r * (r + g)
Determinazione del volume della figura
I lettori potrebbero aver notato che la forma del cono ricorda qualcosa di una piramide, solo la sua superficie laterale è liscia e non nervata, come una piramide. Questa analogia ha una giustificazione geometrica, poiché un aumento del numero di facce laterali della piramide all'infinito lo traduce in un cono. Questo fatto permette di scrivere per il volume di un cono esattamente la stessa formula del volume della piramide. Abbiamo:
V = 1/3 * h * S o
Nota che non importa quale curva chiusa forma la base del cono, anche se la figura è diritta o obliqua, la formula sarà valida in tutti questi casi.
Per un cono di un round, l'espressione di V assume una forma specifica:
V = 1/3 * pi * r 2 * h
Il compito di determinare l'area di un cono attraverso il suo volume
Mostriamo come utilizzare le formule scritte.
Supponiamo che il volume di un cono rotondo sia di 50 cm 3 . È necessario calcolare la sua superficie se il raggio r è tre volte più piccolo dell'altezza h.
Scriviamo la formula per il volume e il rapporto di altezza h con raggio r in base alla condizione del problema:
V = 1/3 * pi * r 2 * h;
h = 3 * r.
Da queste equazioni otteniamo:
V = 1/3 * pi * r 2 * 3 * r =>
r = (V / pi) ≈ 2,516 cm;
h = 3 * ∛ (V / pi) ≈ 7.547 cm.
I valori ottenuti ci permettono di calcolare la lunghezza del generatore g generale del cono:
g = √ (h 2 + r 2 ) = 7.955 cm.
La formula per l'area della superficie della figura è:
S = pi * r * (r + g)
Abbiamo determinato tutte le quantità necessarie (r e g). Sostituendo i loro valori numerici in uguaglianza, otteniamo la risposta: S = 82,72 cm 2 .