Qual è il momento di inerzia: le formule per l'asta e la ruota
Qualsiasi movimento di corpi nello spazio, la cui traiettoria è un cerchio, implica conoscere non solo la velocità angolare, ma anche il momento di inerzia per la descrizione di questo movimento. Qual è il momento di inerzia, così come quello che è uguale per la canna e la ruota, questo articolo risponderà.
Rotazione e momento di inerzia
La quantità fisica, che è chiamata il momento di inerzia, è denotata, di regola, dalla lettera I e appare in fisica quando si considera il momento angolare di un punto materiale, che ruota attorno ad un asse. Il momento angolare L in forma scalare è scritto dalla seguente espressione:
L = r * m * v
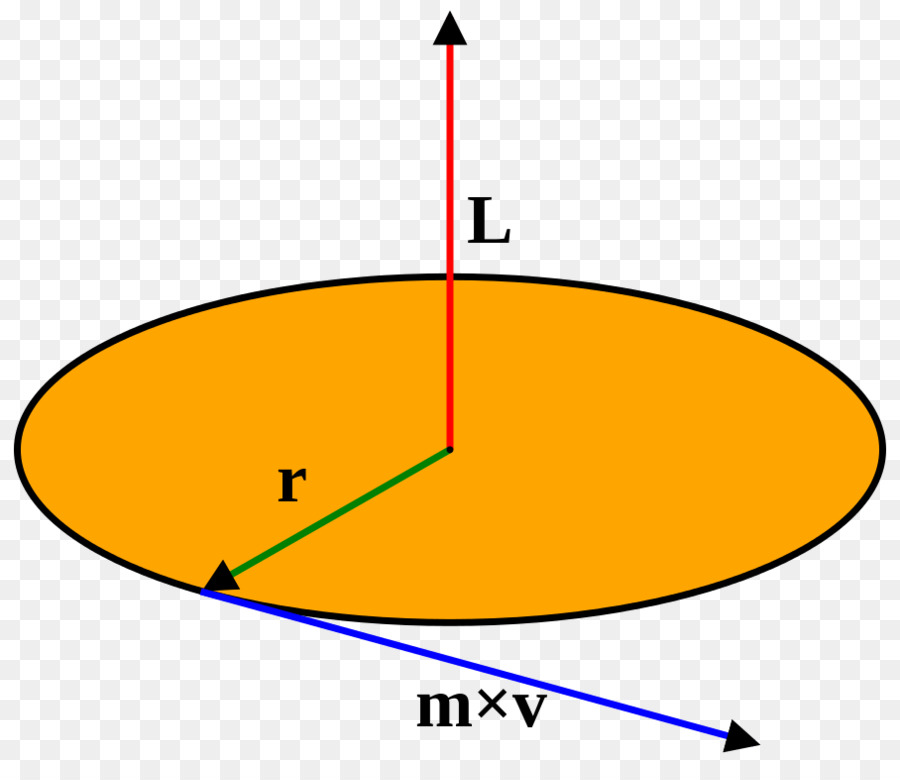
Qui r è la distanza dall'asse del punto materiale, m è la sua massa, v è la velocità lineare. Usando la relazione di quest'ultimo con la velocità angolare ω, otteniamo l'espressione:
L = r 2 * m * ω, dove ω = v / r
Rispondendo alla domanda su quale sia il momento di inerzia, va detto che questo è il valore I = r 2 * m. Cioè, dipende dalla massa dell'oggetto rotante, cresce rapidamente con l'aumentare della distanza dall'asse e viene misurato in kg * m 2 .
Ad
Espressione generale per il momento di inerzia
La formula introdotta nel paragrafo precedente per il valore di I è valida se le dimensioni dell'oggetto sono trascurabili rispetto alla distanza dall'asse r (la Terra ruota attorno alla nostra stella). Se le dimensioni lineari dell'oggetto diventano comparabili con la distanza r, allora è necessario calcolare I per usare una formula più generale, che è riportata di seguito:
I = ∫ m (r 2 * dm)
Mostra che l'integrando è il momento di inerzia del punto materiale. La somma di tutti i momenti da punti con una massa dm è il momento totale di inerzia I per tutto il corpo.
Questa formula è un potente strumento per determinare il corpo I di qualsiasi forma. Secondo la formula, il valore di I è additivo, cioè consente di dividere il corpo in parti separate, calcolare i loro momenti di inerzia e quindi aggiungere i risultati per ottenere il valore del corpo I.
Ad
Il significato fisico di I
Sapendo qual è il momento di inerzia, è necessario dire alcune parole su come il suo valore influenza il comportamento e le caratteristiche della rotazione degli oggetti reali.
Un grande valore di I porta al fatto che il corpo è molto difficile da girare intorno all'asse. Per fare questo, devi svolgere un lavoro significativo e compiere sforzi significativi. Un esempio di un corpo con un grande I è un volano per auto - un disco di metallo pesante montato rigidamente sull'albero motore del motore. Al contrario, se il valore del sistema I è piccolo, può essere rapidamente srotolato e arrestato altrettanto rapidamente e facilmente. Un esempio per questo è il bordo in alluminio di una ruota di bicicletta.
La discussione sopra riportata suggerisce che il momento di inerzia è caratterizzato dall'inerzia del processo di rotazione, cioè svolge lo stesso ruolo della massa del corpo quando viene applicata la forza per impartire l'accelerazione.
La differenza tra la massa e il momento di inerzia non risiede solo nelle unità di misura, ma anche nel fatto che quest'ultima è una funzione del sistema rotazionale e non solo la geometria del corpo e la sua massa.
Il momento di inerzia attorno all'asse di rotazione che interseca il centro di massa dell'asta
Considera un esempio di utilizzo di una formula integrale per risolvere problemi reali. Prima di tutto, risolviamo un semplice problema: c'è una verga sottile di lunghezza l e di massa m. L'asse ruota perpendicolare a questa asta attraverso il centro di massa dell'oggetto. È necessario determinare il valore di I per questo sistema.
Ad

Scriviamo la formula generale per l'inerzia del momento della verga attorno all'asse, abbiamo:
I = ∫ m (r 2 * dm)
Poiché l'asse è perpendicolare al corpo in questione, e l'asta stessa ha uno spessore infinitamente piccolo, è possibile tagliarlo mentalmente in strati sottili con piani paralleli all'asse. In questo caso, troviamo che un elemento di massa dm può essere rappresentato dalla seguente equazione:
dm = ρ * s * dr
Qui ρ è la densità del materiale, S è la sezione trasversale, che è costante e tende a zero (la barra è infinitamente sottile). Sostituisci questa espressione nella formula generale:
I = ρ * S * ∫ + l / 2 -l / 2 (r 2 * dr)
Si noti che i limiti di integrazione sostituiti per r corrispondono alla condizione del problema (l'asse divide l'asta in due parti uguali). Eseguendo l'integrazione, otteniamo:
I = ρ * S * (r 3/3) | + l / 2 -l / 2 = m * l 2/12, dove m = ρ * S * l
Pertanto, il momento di inerzia di un'asta sottile, quando l'asse passa attraverso il centro di massa, è 12 volte inferiore a quello di un punto materiale della stessa massa situato ad una distanza l dall'asse.
Il valore di I per l'asta con l'asse di rotazione alla fine dell'oggetto
Considera quale sia il momento di inerzia, in una situazione leggermente diversa. Abbiamo lo stesso oggetto (asta sottile), ma ora l'asse passa attraverso la fine. Come cambierà il momento di inerzia in questo caso? Usando lo stesso metodo per dividere una barra e la successiva integrazione, come nel paragrafo precedente, otteniamo:
Ad
I = ρ * S * ∫ l 0 (r 2 * dr)
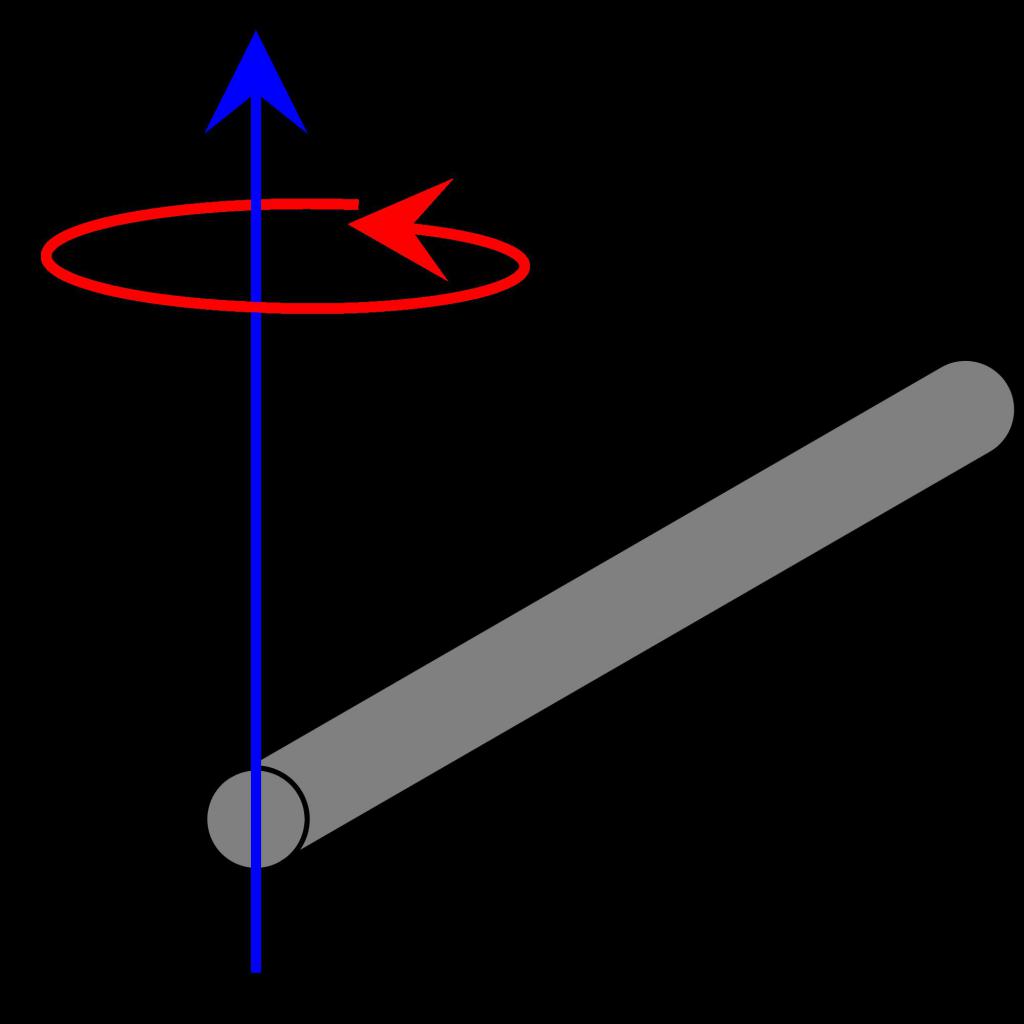
Si noti che sono stati modificati solo i limiti di integrazione. La soluzione è la seguente uguaglianza:
I = m * l 2/3
L'espressione mostra che la stessa asta avrà 4 volte il grande momento di inerzia (più difficile da girare) se l'asse di rotazione viene spostato dal suo centro al bordo.
Considerando la soluzione di questi due problemi, si dovrebbe trarre una conclusione importante: quando si calcola il valore di I, è impossibile ridurre l'intera massa dell'oggetto al suo centro ed eseguire il calcolo come per un punto materiale. Il calcolo dovrebbe essere eseguito solo usando un'espressione integrale.
Valuto per la ruota a raggi
Il momento di inerzia della ruota può essere determinato utilizzando la proprietà di additività della quantità considerata. Per fare questo, smontare mentalmente la ruota in parti separate, che rappresentano i raggi e il cerchio. Poiché un ago è una barra sottile e il suo asse di rotazione attraversa la fine, allora la formula ottenuta nel paragrafo precedente è valida per essa.
Per quanto riguarda il cerchione, il suo momento d'inerzia è simile a quello di un punto materiale situato ad una distanza del raggio della ruota e avente una massa del cerchio.

Aggiungendo i momenti di inerzia di tutti gli elementi, otteniamo:
I = n * m c * r 2/3 + m o * r 2
Qui m c e m o sono i raggi e le masse del cerchio, rispettivamente, n è il numero di raggi. Se tutti i raggi pesano molto meno del cerchio, allora l'inerzia della ruota sarà uguale a:
I = m o * r 2 se n * m c <
La conoscenza del valore di I per la ruota è importante quando si calcola la velocità angolare e il momento angolare di rotazione delle ruote di qualsiasi veicolo (automobile, bicicletta).