Cubo diagonale: che cos'è e come trovarlo?

La diagonale del cubo è uno degli elementi che è necessario conoscere quando si risolvono i problemi nella stereometria durante il completamento del lavoro finale in matematica per il corso di base della scuola.

Qualche teoria dei cubi

Questo poliedro si riferisce direttamente a parallelepipedi e prismi retti. Lui è un caso speciale di entrambi. Alla base del cubo si trova un quadrato, e i suoi bordi laterali sono uguali al lato del quadrato dato. Quindi tutto tre dimensioni avere gli stessi valori

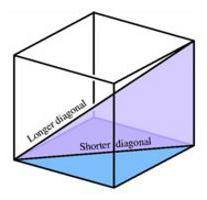
Tutte le sei facce del cubo sono quadrati. La lunghezza di ciascuno dei 12 bordi è la stessa.

In ciascuna delle facce, puoi disegnare una diagonale, la cui lunghezza è facile da trovare usando la formula di Pitagora. Inoltre, il cubo stesso ha una diagonale. Ce ne sono solo quattro. La diagonale del cubo viene disegnata in modo tale da iniziare dalla parte superiore della base inferiore. La fine di questo segmento è nella parte superiore della base superiore, ma in modo da non coincidere con la diagonale del quadrato.

Formule importanti

Dovranno inserire la stessa designazione. Molto spesso la lettera "a" è il lato del cubo. "V" è in volume. "S" e "d" sono rispettivamente l'area e la diagonale. Raggi "R" e "r" delle sfere descritte e inscritte.

V = a³ (# 1) è usato per trovare il volume;

Formula S = a² (# 2) per l'area del viso;

S = 6a² (№3) è necessario per calcolare l'area dell'intera superficie del cubo;

se vuoi conoscere la diagonale di un cubo, la formula sarà tale d = a √ 3 (# 4);

utile per cercare i raggi: R = (a / 2) * √3 e r = a / 2 (n. 5) e (n. 6) .

Alcune parole sulla simmetria del cubo

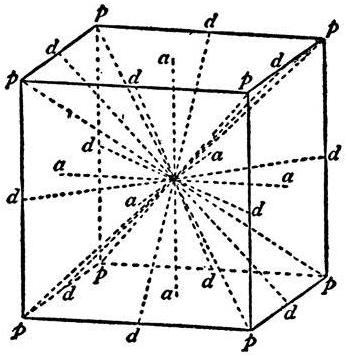
Questo corpo geometrico ha due tipi di simmetria: rispetto a un punto e un asse. Per trovare il primo, devi disegnare una diagonale del cubo, quindi il secondo per trovare il punto della loro intersezione. Lei sarà il centro della simmetria.

Tutte le linee che passano attraverso questo punto e sono perpendicolari ai volti sono gli assi della simmetria.

Esempi di compiti dall'esame

Vengono utilizzati nella parte B, ovvero, dove è necessario eseguire una soluzione di attività dettagliata. Basta scegliere la risposta qui non avrà successo. Pertanto, è necessario conoscere le formule ed essere in grado di applicarle in diverse situazioni.

Il primo gruppo di compiti. Conosce la lunghezza della diagonale del cubo. È necessario calcolare il suo volume o scoprire la superficie.

Ad esempio, un valore noto può essere uguale a uno. Quindi, per scoprire il volume e l'area, è necessario utilizzare le formule n. 1 e 3. Ma stanno parlando del bordo, e data la diagonale. Dovrai scrivere un'altra formula.

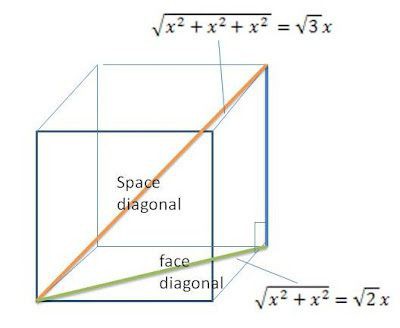
Se guardi il disegno del cubo e la diagonale disegnata in esso, puoi vedere quali forme triangolo rettangolo. Una delle sue gambe coincide con il bordo, la seconda con la diagonale del viso e il cubo diagonale è l'ipotenusa.

Quindi possiamo scrivere il teorema di Pitagora: il quadrato dell'ipotenusa (d ² ) è uguale al quadrato della prima gamba (a ² ), piegato con il quadrato del secondo (a√2) ² . Dopo aver eseguito le trasformazioni, si scopre che il bordo del cubo è così collegato alla diagonale, che è uguale a d diviso per la radice quadrata di 3.

Ora puoi iniziare a trovare il bordo, quindi calcolare il volume e l'area. In un problema specifico, a = 1 / √3 = (√3) / 3. Quindi il volume è uguale a (√3) / 9. L'area è due.

Il secondo gruppo di compiti. Inversa rispetto alla precedente, quando l'area o il volume è noto e si richiede di calcolare il valore della diagonale del cubo.

Un esempio è il problema in cui l'area di superficie è nota ed è uguale a 8. Sarà necessario utilizzare la formula n. 3 e la dipendenza derivata dal problema precedente.

Per prima cosa devi conoscere la lunghezza del bordo. Lei è uguale a radice quadrata dalla S parziale a 6. Dopo aver sostituito una quantità nota, a = √ (8/6) = √ (4/3). Ora resta da calcolare la diagonale del cubo, quadrando questo numero e moltiplicandolo per 3. Ne risulta 2.

Il terzo gruppo di attività contiene dati sulla diagonale della faccia del cubo. Hanno bisogno di riconoscere il volume o l'area del corpo. È anche possibile l'opzione in cui è necessario calcolare la diagonale del cubo. In tali problemi, il ragionamento segue lo stesso percorso considerato nei casi precedenti.