Principio di Dirichlet: problemi con le soluzioni

Ci sono molti principi in matematica. Alcuni di questi sono abbastanza semplici e comprensibili anche per un principiante, e alcuni richiedono alcune spiegazioni e prove. Tuttavia, sono tutti molto efficaci e possono essere applicati facilmente nella pratica. Uno di questi è il principio di Dirichlet (noto anche come principio del piccione / coniglio). Questa è una dichiarazione abbastanza semplice che può aiutare a risolvere molti problemi matematici.

Storia di

Questo principio fu formulato dal matematico onorario tedesco Johann Dirichlet nel 1834. Oggi è usato in combinatoria, così come in fisica matematica. Tradotto dal tedesco originale, suona come il "principio delle scatole". Lo scienziato ha condotto la sua ricerca con conigli e contenitori. Ha dimostrato che se mettiamo, diciamo, 5 conigli in 7 contenitori, allora almeno in un contenitore ci sarebbe 5/7 da un animale. Tuttavia, il coniglio non può essere diviso in parti, quindi almeno una cella sarà vuota (5/7 è 0 numeri interi). Allo stesso modo, nella direzione opposta, se ci sono 7 conigli e 5 scatole, allora almeno uno di loro ha 2 conigli (7/5 è 2 intatti). Partendo da questa affermazione, la matematica è riuscita a formulare un principio che garantisce da anni una soluzione efficace dei problemi matematici.

Formulazione e prova moderne

Oggi ci sono diverse formulazioni di questo principio. Il più comprensibile e semplice significa che è impossibile piantare 8 conigli in 3 gabbie in modo che ciascuno non ne abbia più di 2. Una formulazione più scientifica e complessa che spiega il principio di Dirichlet dice: se ci sono k + 1 conigli nelle cellule k, allora almeno Almeno 1 cellula conterrà più di una lepre. E se ci sono k-1 lepri nelle cellule k, allora almeno 1 cella conterrà meno di una lepre. La dimostrazione di questa affermazione è piuttosto semplice, per così dire, per contraddizione. Se assumiamo che ci siano meno lepri in ogni cellula di k-1 / k, allora k di celle di lepre è minore di k * k-1 / k = k-1, che contraddice le condizioni iniziali.

In realtà, un principio così semplice e comprensibile facilita enormemente la soluzione dei problemi matematici e la dimostrazione di molti teoremi laboriosi. È solo necessario tenere conto che le lepri e le celle possono essere facilmente sostituite con oggetti e oggetti matematici (numeri, punti, segmenti, figure, ecc.).

Un'altra formulazione

A volte i compiti sul principio di Dirichlet non sono così semplici ed evidenti come con gli animali nelle scatole. È necessario trasferire questo principio agli insiemi matematici per trovare soluzioni. In questo caso, puoi fare affidamento su una formulazione diversa e più complessa.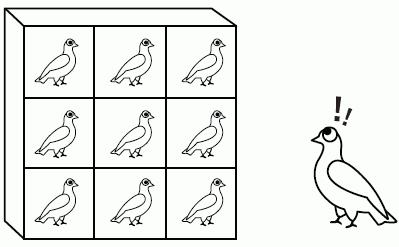

Se mappiamo l'insieme S contenente d + 1 elementi all'insieme R con l'insieme di elementi d, allora due elementi dell'insieme S avranno la stessa immagine.

Sebbene il GEF moderno in matematica imponga richieste creative agli studenti e offra opzioni non standard, la soluzione attraverso l'asserzione di Dirichlet non è sempre così semplice e diretta. A volte è molto difficile determinare quale valore considerare come animale e quale gabbia e come il fatto di avere due animali in una gabbia aiuti a risolvere il problema. E se riusciamo a capirlo, è ancora impossibile determinare in quale cella particolare sarà l'oggetto. Cioè, puoi semplicemente provare l'esistenza di una tale cellula, ma non puoi concretizzarla.

Esempio numero 1. Geometria

Gli esempi moderni di soluzione dei problemi dimostrano che i vari oggetti matematici perfetti possono agire come animali e cellule.

compito

La linea k passa attraverso il piano del triangolo ABC, ma non interseca nessuno dei suoi vertici. È necessario dimostrare che non può attraversare i suoi tre lati.

decisione

Immagina come la linea k divide il triangolo in due piani, chiamiamoli s1 e s2. Supponiamo che s1 e s2 siano aperti, cioè che non contengano la linea k. Bene, ora è il momento di applicare il principio di Dirichlet. Compiti con soluzioni possono dimostrare che in condizioni moderne conigli e cellule significano vari oggetti. Quindi, invece di lepri, sostituiamo i vertici del triangolo e invece delle celle - il mezzo piano. Poiché la linea disegnata k non interseca nessuno dei vertici, ognuno di essi si trova in uno o in un altro piano. Ma dal momento che ci sono tre vertici nel triangolo e abbiamo solo due piani (s1 e s2), uno di essi conterrà due vertici. Supponiamo che questi siano i vertici A e B, e si trovino nel mezzo piano s2 (cioè, si trovano sullo stesso lato di k). In questo caso, il segmento AB non interseca la retta k. Cioè, c'è un lato nel triangolo che k non interseca.

Soluzione alternativa

In questo problema, abbiamo assunto che i punti A e B si trovassero nello stesso piano, ma il principio di Dirichlet non indica una cella specifica, quindi potremmo anche indicare che i vertici C e B, o A e C erano situati nello stesso piano. non importa da quale parte del triangolo si interseca la linea retta k. Pertanto, questo principio è ideale per la sua soluzione.

Esempio n. 2. Geometria

compito

Nel mezzo di un triangolo equilatero ABC (in cui AB = BC = AC = 1) sono stati individuati 5 punti. È necessario dimostrare che due di loro si trovano a una distanza inferiore a 0,5.

decisione

Se disegni le linee di mezzo nel triangolo ABC destro, lo dividono in 4 piccoli triangoli rettangoli con lati ½ = 0,5. Supponiamo che questi triangoli siano cellule e che i punti al loro interno siano conigli. Si scopre che abbiamo 5 conigli e 4 cellule, quindi, in uno di questi ci saranno almeno due conigli. Dato che i punti non sono vertici (poiché si trovano all'interno del triangolo ABC, e non su uno dei suoi lati), saranno posizionati all'interno di piccole figure. Di conseguenza, la distanza tra loro sarà inferiore a 0,5 (poiché la dimensione del segmento all'interno del triangolo non supera mai la dimensione del suo lato maggiore).

Esempio numero 3. Combinatorics

In altri campi, il principio di Dirichlet può anche essere applicato con successo: la combinatoria e la fisica matematica sono da tempo basate su di essa per risolvere i problemi.

compito

Ad esempio, attorno a un tavolo arrotondato, m bandiere di paesi diversi si trovano a uguale distanza l'una dall'altra, e m rappresentanti di ogni paese siedono al tavolo, ognuno di essi si trova accanto alla bandiera di qualcun altro. È necessario dimostrare che con una certa rotazione del tavolo almeno due dei rappresentanti saranno vicini alle loro bandiere.

decisione

Si scopre che ci sono m-1 modi per espandere la tabella in modo che la disposizione reciproca di rappresentanti e bandiere cambi (se escludiamo il posizionamento iniziale della tabella), ma ci sono m rappresentanti rimasti.

Applichiamo l'asserzione di Dirichlet alla soluzione e denotiamo che i rappresentanti sono conigli, e alcune posizioni del tavolo durante la rotazione sono celle. In questo caso, è necessario tracciare un'analogia tra la posizione del rappresentante accanto alla bandiera corrispondente e le celle riempite. Cioè, un risultato positivo (1 rappresentante è posto vicino alla sua bandiera) equivale al risultato "il coniglio è nella gabbia". Comprendiamo che abbiamo una cella inferiore a quella necessaria (m-1), il che significa che uno di loro avrà almeno 2 conigli. Allo stesso tempo, non è escluso che alcune gabbie siano vuote (non un solo rappresentante corrisponde alla bandiera), ma in alcune gabbie ci saranno due, tre o anche più conigli (due, tre o più rappresentanti coincideranno con le bandiere). Quindi, con una certa rotazione, almeno due rappresentanti si troveranno vicino alle loro bandiere (almeno due conigli cadranno in una cella).

Iniziando la soluzione di tale problema, è importante capire che la posizione iniziale è anche una cella, ma in base alla condizione del problema è ovviamente vuota, quindi riduciamo il totale di 1 (m-1).

Esempio numero 4. Teoria dei numeri

Il principio di Dirichlet nella teoria dei numeri è anche di fondamentale importanza.

compito

Supponiamo, su un pezzo di quaderno in una gabbia, uno studente a caso ai nodi delle celle ponga 5 punti. È necessario dimostrare che almeno un segmento con vertici in questi punti passa attraverso il nodo della cella.

decisione

Per prima cosa è necessario raffigurare su un foglio di quaderno il sistema di coordinate, la cui base si trova in uno dei nodi. Gli assi del sistema di coordinate coincideranno con le linee della griglia e il lato della cella verrà considerato come un singolo segmento. Si scopre che tutti i 5 punti segnati saranno nel sistema e le loro coordinate saranno solo un numero intero (pari o dispari). Quindi, otteniamo 4 opzioni di coordinate: (pari, pari), (dispari, pari), (pari, dispari) e (dispari, dispari). Quindi, 2 punti su 5 corrisponderanno a una variante. Se si guarda la situazione dalla posizione di Dirichlet, allora è necessario designare i punti come lepri e le opzioni di coordinate - come celle. Otteniamo 5 piccioni con una fava e 4 gabbie, rispettivamente, in una di queste ci saranno almeno 2 animali. Supponiamo che questi siano i punti P e A, con le coordinate (x ₄ , y ₃ ) e (x ₅ , y ₆ ). La parte centrale del segmento che collega questi due vertici avrà coordinate ((x ₄ + x ₅ ) / 2), ((y ₃ + y ₆ ) / 2)), che saranno numeri interi nelle condizioni della parità corrispondente x ₄ e x _5, y ₃ e y ₆ . Si scopre che il centro del segmento si trova nel nodo della cella.

Esempio numero 5

Un sacco di compiti di diversa complessità possono essere risolti attraverso il principio di Dirichlet. I problemi con soluzioni di varie domande matematiche e logiche si basano spesso su questo principio.

compito

Sulla strada diritta scavavano piccoli solchi trasversali. La distanza tra tutte le scanalature è uguale e uguale a Ö2 m. È necessario dimostrare che, indipendentemente dalla larghezza delle scanalature, una persona che cammina lungo la strada a intervalli di 1 m cadrà una volta in una di esse.

decisione

Per facilitare la soluzione, è necessario immaginare che la strada possa essere "ferita" su un cerchio con una lunghezza di Ö2 metri. Si scopre che tutte le scanalature si fonderanno in 2 opposte, e i passi della persona verranno visualizzati sotto forma di un arco pari a 1 m. Dobbiamo successivamente contrassegnare tutti i passaggi finché uno di essi si trova nell'arco che indica il solco, indipendentemente dalla lunghezza k arco (larghezza della scanalatura). Certo, è ovvio che se un uomo percorreva una distanza uguale a meno di k, allora prima o poi sarebbe entrato in un fosso. Dopo tutto, una persona non riesce a superare la distanza k se la sua lunghezza del passo è inferiore a k. Quindi, dobbiamo trovare due tracce, la distanza tra le quali non supererà il valore di k. Per fare ciò, sarebbe opportuno utilizzare il principio di Dirichlet. Dividiamo mentalmente l'intero cerchio in archi di dimensioni inferiori a k ​​e li considereremo come celle. Supponiamo che ce ne siano n. Supponiamo che il numero di passi sia maggiore del numero di archi (n + m), sebbene due passi non coincideranno a causa dell'irrazionalità del numero Ö2, quindi secondo il principio di Dirichlet, almeno una delle celle conterrà più di un passo. E poiché la lunghezza dell'arco è inferiore a k, la distanza tra i passaggi sarà inferiore. Pertanto, abbiamo trovato i passaggi necessari per la dimostrazione.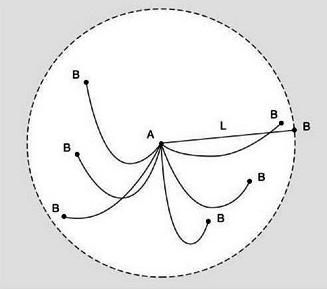

Generalizzazione del principio

I materiali sulla matematica, oltre alle formulazioni standard (semplici e poco), contengono anche una generalizzazione, che viene utilizzata per identificare più di due oggetti simili tra loro. Sostiene che se dm + 1 conigli sono posti in cellule d, allora almeno m + 1 conigli saranno nella stessa cella.

Esempio n. 6. Generalizzazione

compito

Un rettangolo con un'area di 5 x 6 celle (30 celle), solo ombreggiato 19. È possibile trovare un quadrato con un'area di 2 x 2 celle in cui ne saranno verniciate almeno tre?

decisione

La nostra figura deve essere divisa in 6 blocchi di 5 celle. Sulla base della dichiarazione di Dirichlet, almeno 4 celle saranno dipinte in una di esse (19/6 = 4). Quindi in uno dei quadrati con un'area di 4 celle, situata in uno dei blocchi, verranno dipinte almeno 3 celle.

Esempio numero 7

Classe in cui 25 persone. Di 3 studenti selezionati a caso, due saranno amici. È necessario dimostrare che nella classe c'è uno scolaro che ha più di 11 amici.

Due soluzioni

Per cominciare, prendiamo due scolari che non sono amichevoli tra loro (poiché se fossero tutti amici tra loro, ci sarebbero tre amici in ogni troica e ogni studente sarebbe amico di altri 24). I rimanenti 23 compagni di classe saranno amici di uno dei nostri due, perché altrimenti ci sarebbe una troica senza amici (e questo contraddice la condizione originale del problema). Si scopre che uno dei due studenti sarà amico di almeno 12 studenti. In questo caso, gli studenti sono conigli e i termini "amici o meno" sono celle. Abbiamo 23 animali e solo 2 gabbie. Di conseguenza, in uno di essi almeno 23/2 = 11,5, cioè 12 conigli. Cioè, uno dei 2 studenti scelti da noi sarà amico di almeno 12 dei loro compagni di classe (o anche di più). Certo, ci sono altri metodi per risolvere il problema, ma questo è uno dei più comprensibili e convenienti.