Come calcolare gli angoli tra una linea e un piano?
Quando si studia un corso scolastico di geometria nello spazio bidimensionale, viene dedicato molto tempo al considerare il comportamento delle linee rette. Quando si rivolgono allo studio della stereometria nei gradi superiori, i temi dei piani e delle linee rette nello spazio vengono alla ribalta. Questo articolo tratta di una di queste domande. Vale a dire, l'argomento del calcolo tra piani e angoli retti e distanze.
Linea retta su un piano e modi di impostazione
Per risolvere con successo problemi computazionali tra linee rette e piani di angoli e distanze, è necessario imparare come impostare matematicamente questi oggetti geometrici, oltre a padroneggiare i metodi di lavoro con le equazioni corrispondenti. Iniziamo specificando le linee sull'aereo.
Ogni studente conosce la seguente formula:
y = k * x + b
Lavorare con esso è abbastanza conveniente nello spazio bidimensionale. È facile da usare per disegnare una linea retta in un sistema di coordinate rettangolare. Inoltre, la conoscenza del coefficiente k per ciascuno di essi ci consente di dire se saranno paralleli o se si intersecano (per parallelo, i loro coefficienti k sono uguali).
Ad
Se scriviamo l'espressione data in una forma leggermente diversa, otteniamo una formula di un tipo generale per una linea retta. La sua forma è la seguente:
A * x + B * y + C = 0
Ovviamente, usando semplici trasformazioni, puoi ottenere la prima espressione da essa.
Le formule scritte possono anche essere utilizzate per calcolare l'angolo di intersezione delle linee rette. Tuttavia, ciò richiede un numero di trasformazioni, il che è inopportuno. Pertanto, quando l'attività richiede di trovare un angolo, è preferibile utilizzare la forma vettoriale di rappresentazione della linea. La sua visione può essere scritta come:
(x; y) = (x 0 ; y 0 ) + λ * (a; b)
In questa uguaglianza, le coordinate X e Y con indici di zero descrivono la posizione di un punto attraverso il quale passa la linea. I valori di aeb sono le coordinate del vettore che giace su di esso. Può essere diretto sia in una direzione che nell'altra, la linea retta non cambia. Questo vettore è chiamato vettore guida, poiché determina in modo univoco la distribuzione di una retta su un piano. Lambda λ è un parametro che prende un valore arbitrario dall'insieme di numeri reali.
Ad
Notiamo che la forma vettoriale del record è notevole, che contiene chiaramente un segmento diretto di una linea retta, le cui coordinate sono usate per determinare l'angolo tra due linee rette sul piano.
Retta nello spazio tridimensionale
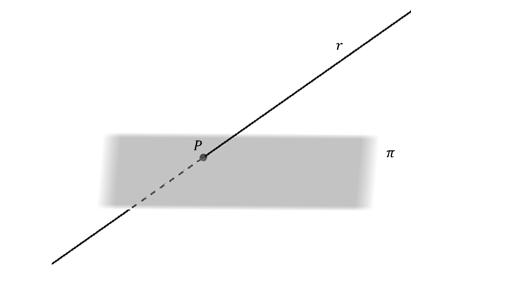
Nello spazio descritto dai tre assi coordinati, la linea retta è definita in forma generale come l'intersezione dei piani. Qui, dato l'argomento dell'articolo, consideriamo solo l'equazione vettoriale. È simile a quello del caso piatto, ma con l'aggiunta della terza coordinata:
(x; y; z) = (x 0 ; y 0 ; z 0 ) + λ * (a; b; c)
Quando si risolvono i problemi, questa espressione è utile per aprire e applicare in una forma parametrica:
x = x 0 + λ * a;
y = y 0 + λ * b;
z = z 0 + λ * c
Si noti che il valore del parametro λ, sebbene arbitrario, dipenderà da tutte e tre le uguaglianze.
Descrizione dell'aereo
Così come per una linea retta, per un aereo ci sono anche diversi modi per definirlo. Considera solo due di essi che sono importanti da sapere per poter risolvere i problemi nella pratica.
Il primo metodo di assegnazione è di portare un'equazione di tipo generale. È simile all'espressione corrispondente per la linea retta nel caso bidimensionale:
A * x + B * y + C * z + D = 0
La combinazione dei primi tre coefficienti è le coordinate del vettore di direzione per questo piano. Di regola, è denotato dal simbolo n¯, cioè:
n ¯ = (A; B; C)
Il quarto coefficiente D determina la distanza tra i piani paralleli che hanno i primi tre coefficienti identici.
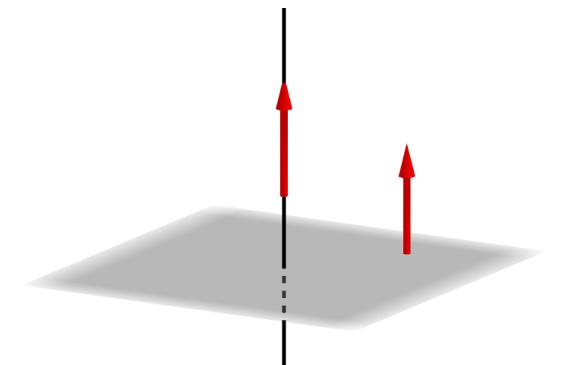
Poiché il vettore nì giace sul piano normale, è perpendicolare a qualsiasi vettore e retta costruita sui suoi due punti arbitrari. Conoscere le coordinate di n ¯ è fondamentale per determinare tra linee rette e angoli di angoli.
Il secondo modo per definire un piano è una forma parametrica vettoriale dell'equazione. È scritto in questo modo:
(x; y; z) = (x 0 ; y 0 ; z 0 ) + λ * (a 1 ; b 1 ; c 1 ) + γ * (a 2 ; b 2 ; c 2 )
Questa uguaglianza riflette il fatto che due linee rette definiscono un piano nello spazio in modo univoco. Qui, il secondo e il terzo termine indicano due vettori di direzione per le rette arbitrarie che appartengono al piano.
Ad
Il vettore normale n ¯ non è esplicitamente contenuto per questa forma di scrittura, ma è facile da calcolare:
n¯ = [(a 1 ; b 1 ; c 1 ) * (a 2 ; b 2 ; c 2 )]
Angolo tra linee rette
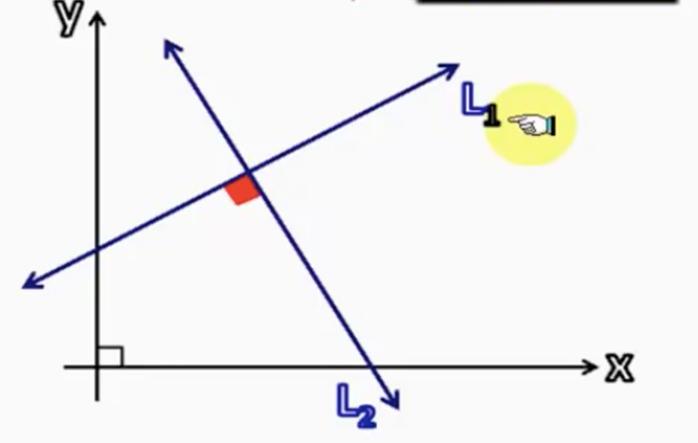
Se le uguaglianze vettoriali di ciascuna delle linee rette sono note, l'angolo tra di esse è semplice. Per fare ciò, è sufficiente utilizzare le proprietà del prodotto scalare per i segmenti guida delle linee rette. Se le guide vettoriali sono denotate dai simboli v ¯ e ¯, allora la formula richiesta assumerà la forma:
α = arccos (| (v¯ * u¯) | / (| v¯ | * | u¯ |)))
Poiché nel caso dell'intersezione di linee rette vengono formate due coppie di angoli uguali, allora viene preso un angolo acuto come il vero angolo tra di loro. Per questo motivo, la formula contiene il segno del modulo nel numeratore.
Questa formula per un caso bidimensionale è sempre valida. Il valore risultante di 0 o dice che le linee rette non si intersecano, ma sono parallele.
Per quanto riguarda il caso nello spazio, oltre al calcolo mediante la formula, è necessario effettuare calcoli aggiuntivi. Sono associati alla ricerca del punto di intersezione degli oggetti in questione. Il fatto è che nello spazio si può ottenere il valore finale dell'angolo α, ma le rette non si intersecano, poiché possono essere incrociate.
Ad
Piano, linea e angolo della loro intersezione
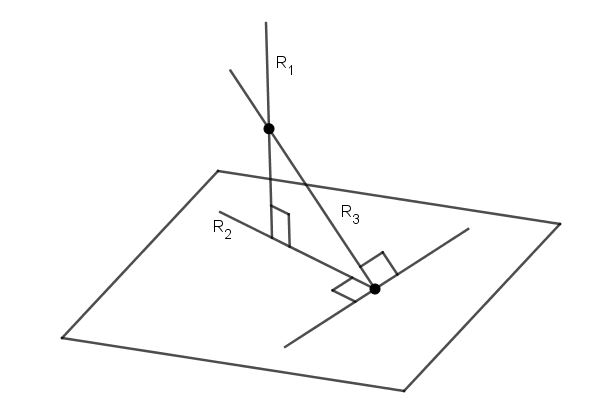
Per trovare l'angolo tra una retta e un piano, è sufficiente conoscere l'equazione per ciascuno di questi oggetti. L'angolo tra loro è l'angolo di due linee intersecanti, una delle quali è l'originale, e l'altra appartiene al piano ed è la proiezione della linea originale su di essa. La figura seguente mostra il piano che la retta interseca con un angolo α.
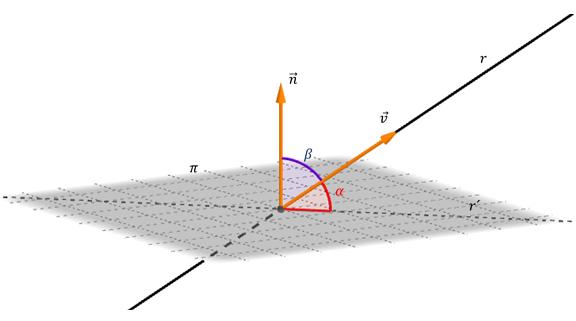
Se il vettore di direzione per un vettore diretto è indicato con v ¯, e il normale per il piano è n ¯ (si veda la figura), Quindi il calcolo dell'angolo α è ottenuto dalla formula:
α = arcsin (| (v¯ * n¯) | / (| v¯ | * | n¯ |)))
Si noti che in questa formula, a differenza di un'espressione simile per due linee rette che si intersecano, viene utilizzata la funzione arcoseno, non la funzione arcoseno.
La distanza tra le linee rette su un piano e un piano e una linea retta nello spazio
Per calcolare la distanza tra gli oggetti in questione in geometria c'è un insieme di formule. L'applicazione di un'espressione da esso dipende dalla forma in cui sono forniti il piano e la linea.
Ad
Se due linee rette sono date in forma generale su un piano, allora la distanza tra loro può essere calcolata come segue:
d = | A * x 1 + B * y 1 + C | / √ (A 2 + B 2 )
Qui x 1 e y 1 sono le coordinate di un punto arbitrario su una linea retta, ei coefficienti A, B, C sono presi per l'altra retta. Questa formula è valida se le linee sono parallele tra loro. Se si intersecano, la distanza è zero.
La distanza tra la linea e l'aereo che lo attraversa è zero. Se la retta è parallela al piano, la distanza corrispondente viene calcolata come:
d = | A * x 1 + B * y 1 + C * z 1 + D | / √ (A 2 + B 2 + C 2 )
Dove le coordinate appartengono a un punto arbitrario sulla linea.
Compito: determinare l'angolo tra una retta e un piano
Dato una linea retta e un piano:
(x; y; z) = (1; 2; 0) + λ * (- 1; 1; 4);
-5 * x + y - 3 = 0
Qual è l'angolo tra una linea retta e un piano?
Scriviamo le guide del vettore v ¯ e n ¯:
v = (-1; 1; 4);
n¯ = (-5; 1; 0)
Sostituiscili nella formula appropriata per α, otteniamo:
α = arcsin (| 5 + 1 + 0 | / (√18 * √26)) ≈ 16,1 o
Compito: trova la distanza tra le linee rette
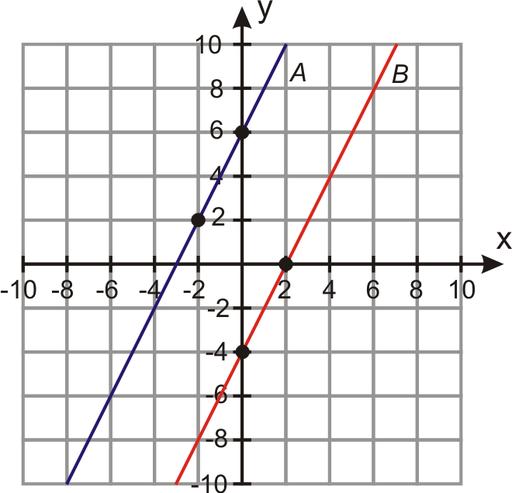
Considerate due equazioni di linee rette nello spazio bidimensionale:
y = 3 * x - 1;
y = 3 * x + 3
Qual è la distanza tra loro?
Poiché i coefficienti k per entrambi gli oggetti sono uguali (pari a 3), si verifica il caso delle rette parallele.
Per calcolare la distanza tra loro, prendere un punto arbitrario della prima retta e riscrivere la seconda equazione in generale, abbiamo:
coordinate del punto (0; -1);
3 * x - y + 3 = 0, cioè A = 3, B = -1, C = 3
Ora questi valori possono essere sostituiti nella formula appropriata:
d = | 3 * 0 -1 * (- 1) + 3 | / √ (9 +1) = 4 / √10 ≈ 1.265
La risposta è ricevuta in unità di questo sistema di coordinate.