Misura dell'indice di rifrazione del vetro. Lavoro di laboratorio

La conoscenza dell'indice di rifrazione di un particolare vetro è importante per il suo uso come materiale per lenti ottiche. In questo articolo presentiamo il lavoro di laboratorio sulla misurazione dell'indice di rifrazione del vetro, avendo considerato tutte le formule necessarie lungo la strada.

Lo scopo e gli obiettivi del lavoro di laboratorio

La misurazione di laboratorio dell'indice di rifrazione del vetro mira a raggiungere il seguente obiettivo: apprendere come misurare le caratteristiche di rifrazione dei materiali trasparenti e elaborare i risultati.

Nel corso del lavoro, dovrebbero essere risolti i seguenti compiti:

• Studiare il materiale teorico.
• Studiare l'impostazione sperimentale e i suoi principi operativi.
• Per calcolare gli angoli di incidenza e rifrazione.
• Determina l'angolo critico.
• Trova il valore dell'indice di rifrazione per il vetro, elaborando i risultati.
• Trarre conclusioni sul lavoro.

Teoria del fenomeno della rifrazione

Questo fenomeno consiste nel cambiare la direzione del movimento rettilineo del fascio di luce quando si sposta da un mezzo trasparente a un altro. Tale situazione si presenta, ad esempio, quando la luce attraversa il confine acqua - aria o vetro - aria.

Le leggi di rifrazione interessarono l'umanità nel corso della sua storia. Erano impegnati negli antichi greci (Tolomeo, I-II secolo d.C.), gli arabi nel Medioevo (Ibn Sahl, X secolo), così come molti scienziati nella nuova epoca (Huygens, Newton, Descartes, Snell). Allo stato attuale, si ritiene che l'olandese Snell abbia prima formulato la legge della rifrazione in una forma moderna, riassumendo molti dati sperimentali.

La formula per il fenomeno della rifrazione ha la seguente forma:

n ₁ * sin (θ ₁ ) = n ₂ * sin (θ ₂ ) = const.

Qui θ ₁ è l'angolo relativo alla normale all'interfaccia tra il mezzo su cui il raggio colpisce questa superficie, θ ₂ è l'angolo relativo alla stessa normale per il raggio rifratto. I valori di n ₁ , n ₂ sono gli indici di rifrazione dei media 1 e 2, rispettivamente. L'indicatore n determina quanto fortemente il mezzo rallenta la velocità della luce rispetto a quello nel vuoto, cioè:

n = c / v, c è la velocità della luce nel vuoto, v è nel mezzo.

Angolo critico

La legge di Snell dimostra che l'angolo di incidenza è maggiore dell'angolo di rifrazione se il primo mezzo è otticamente meno denso (n ₁ 2). Il contrario è anche vero.

Quando il raggio si muove in un mezzo otticamente più denso e passa attraverso l'interfaccia tra il mezzo in una sostanza trasparente meno densa, allora c'è un angolo in cui il raggio rifratto si muoverà lungo la superficie che separa il mezzo. Questo angolo è fondamentale Qualsiasi angolo di incidenza maggiore di quello porterà al fatto che nessuna parte della luce passa attraverso l'interfaccia. Questo fenomeno è chiamato la piena riflessione interna.

Data la legge di Snell e le spiegazioni di cui sopra, per un angolo critico puoi scrivere:

θ ₁ = arcsin (n ₂ / n ₁ ), dove n ₁ > n ₂ .

Questo fenomeno viene utilizzato in fibra ottica per trasmettere energia elettromagnetica su lunghe distanze senza perdita.

Configurazione sperimentale

La determinazione dell'indice di rifrazione del vetro viene eseguita utilizzando l'installazione, che è mostrata nella figura sottostante.

I numeri nella foto indicano quanto segue:

1. Linea graduata, su cui si trovano i principali dispositivi di lavoro dell'impianto.
2. La fonte di energia elettrica.
3. La lampada, che è la fonte di luce.
4. Un obiettivo di raccolta con una lunghezza focale nota (ad esempio, 10 cm).
5. Cassetta per diaframmi.
6. Apertura sotto forma di reticolo (le aperture servono a focalizzare meglio il raggio di luce).
7. Disco graduato ottico
8. Oggetto di vetro, il cui indice di rifrazione deve essere misurato. Ha la forma di un semi-cilindro, cioè le sue tre superfici sono piani, e il quarto è cilindrico.
9. Prisma ottico (non utilizzato per questo lavoro di laboratorio).

Perché è necessario utilizzare un oggetto di vetro nella forma di un mezzo cilindro, verrà spiegato di seguito.

Preparazione dell'installazione per il funzionamento

Il principio di funzionamento dell'impianto per la misura sperimentale dell'indice di rifrazione del vetro è estremamente semplice: basta formare un fascio di luce stretto, inviarlo parallelamente al disco ottico attraverso un mezzo cilindro di vetro e, usando la graduazione del disco, misurare l'angolo di incidenza e l'angolo di rifrazione.

La preparazione per l'installazione viene eseguita in sequenza:

1. Posizionare la sorgente luminosa (lampada) sul righello graduato nella posizione "0 cm".
2. Posiziona il corpo con una lente di raccolta su un righello graduato in una posizione uguale alla lunghezza focale. In questo caso, 10 cm. A causa di questa posizione, tutti i raggi che la lampada emette dalla lente usciranno parallelamente al righello graduato.
3. Accendere la fonte di alimentazione e, regolando la posizione dei diaframmi, assicurarsi che il raggio di luce sia il più stretto possibile. Lo spessore dovrebbe essere molto inferiore alla divisione più piccola sul disco ottico.
4. Regola l'altezza della posizione del disco ottico in modo che il raggio di luce passi su di esso, quasi a toccarne la superficie. Il disco dovrebbe anche essere regolato rispetto all'asse laterale in modo che il raggio passi esattamente attraverso il suo centro, cioè attraverso uno dei diametri.
5. Al centro del disco, è necessario inserire un semicilindro di vetro in modo che il piano laterale coincida con uno dei diametri del disco.

La configurazione è pronta per l'esperimento.

Condurre un esperimento

Il lavoro del laboratorio "Misura dell'indice di rifrazione del vetro" si compone di due fasi. Per prima cosa, conduci un esperimento per spostare il raggio di luce dall'aria al vetro e poi dal vetro all'aria:

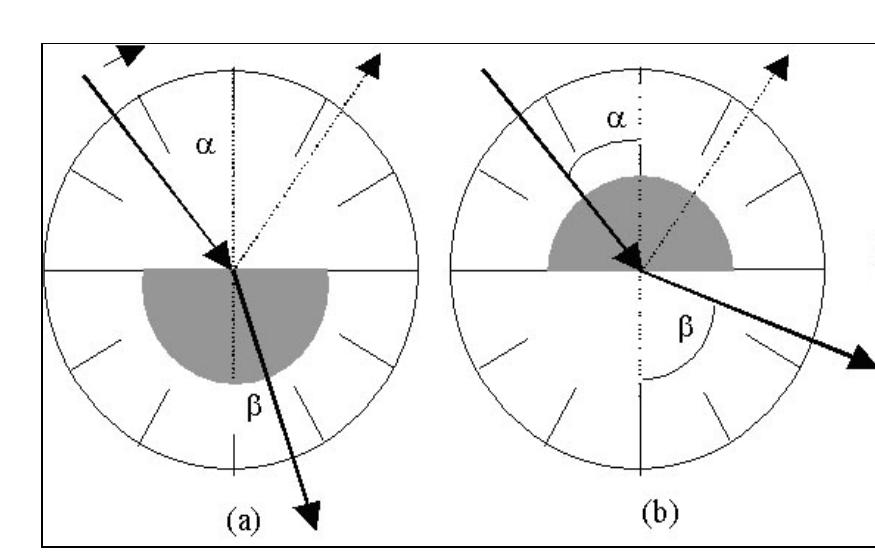
• Dall'aria al vetro. Innanzitutto, è necessario ruotare il disco ottico in modo che dopo aver attraversato il mezzo cilindro, il raggio non si rifrange. Questa posizione corrisponderà all'origine (0 ^o ). Successivamente, è necessario ruotare il disco per ogni 5 ^o e inserire i dati nella tabella corrispondente: α e β - gli angoli di incidenza e rifrazione. È necessario condurre circa 10-15 misurazioni. La posizione del mezzo cilindro sul disco può essere visualizzata nella figura seguente (a).
• Dal vetro all'aria. In questo caso, il disco con il semicilindro deve essere ruotato di 180 ^o . In questo caso, il raggio incidente cadrà per prima cosa su una superficie cilindrica. Poiché cade su di esso lungo il raggio (con un angolo di 90 ^° ), non si verifica alcuna rifrazione all'ingresso del vetro, e si verifica solo all'uscita da esso attraverso una superficie piana. Questa situazione è illustrata nella figura seguente (b). Scegliendo un punto di riferimento come nel caso precedente, dovresti girare il disco ogni 5 ^o e misurare gli angoli.

Quando viene eseguito l'esperimento "vetro-aria", si verifica una situazione ad un certo angolo di incidenza del raggio quando non esce attraverso la superficie piatta del mezzo cilindro. Questo angolo è fondamentale

Elaborazione dei risultati

Per ogni coppia di angoli α e β, calcolare il valore di n _i per il vetro. Questo viene fatto usando le formule per misurare l'indice di rifrazione del vetro. La soluzione dalla legge di Snell è la seguente:

• Dall'aria al vetro: n _i = n _v * sin (α) / sin (β).
• Dal vetro all'aria: n _i = n _v * sin (β) / sin (α).

L'indice di rifrazione dell'aria è pari a n _v = 1.00029.

Quindi, otteniamo una serie di valori di n (il loro numero è uguale al numero totale di misurazioni effettuate). Lascia che questo numero sia m. Ora è necessario trovare il valore medio per l'indice di rifrazione del vetro n ¯, così come la varianza Δn (deviazione quadratica media), mostrando la precisione dell'esperimento. Questi valori sono determinati dalle seguenti formule:

n ¯ = Σ _{i = 1} ^m (n _i ) / m;

Δn = √ (Σ _{i = 1} ^m (n _i -n¯) ² / m).

Il risultato finale è scritto nel modulo:

n ¯ ± Δn.

Conclusioni sul lavoro di laboratorio

Avendo eseguito il lavoro "Misura dell'indice di rifrazione del vetro", le conclusioni possono essere tratte come segue:

• il raggio di luce subisce la rifrazione al passaggio su un altro mezzo;
• l'angolo critico sorge solo nel caso della transizione della luce dal vetro all'aria, ma non viceversa;
• per l'affidabilità del risultato ottenuto, devono essere effettuate diverse misurazioni (più di 10), quindi il valore finale deve essere presentato come valore medio, indicando il limite della sua precisione.